0 - ABSTRACT
许多计算机任务在缺少上下文信息的情况下的处理会更加困难。例如,在多相机跟踪任务下,行人可能在不同照相机下面因为有这不同的姿势和灯光条件而看起来很不一样。类似地,在低分辨率高角度监控视频中,头部方向评估也是一个挑战。如果没有上下文信息,人们在处理此类任务时会有很大麻烦。在我们的工作中,我们将上下文信息、社会群体信息和两个重要的计算机视觉任务:多目标跟踪和监控视频的头部姿态和方向评估进行结合。这三部分都采用一个概率公式进行建模并且我们提出了有效的解决方案。在多相机跟踪和头部姿势评估中,我们展示了社会群体信息有效地减少了视觉模糊。我们进一步意识到在单相机多目标跟踪中,社会群体信息提供了一个自然的高阶关联从而避免了现有的复杂的高阶轨迹关联算法。在实验过程中。我们展示了我们的模型比没有社会群体上下文信息的模型的改进,以及几种关于追踪、头部姿势评估以及群体发现的在公开有效的数据集上的先进方法。
1 - INTRODUCTION
对于许多计算机视觉任务,纯粹地使用视觉信息很难得到令人满意的效果,这是因为在现实世界中图像和视频固有的视觉模糊。以多相机追踪为例。特定的一个行人在多个相机下由于不同的条件而看起来很不一样。另一个例子是在高角度监控视频下的头部姿势评估。(在这种情况下我们主要研究偏航角估计。)人头图像通常来说是低分辨率的,这使得视觉感受是不可靠的(见于图1)。因此,上下文信息对于这些任务来说是必要的。

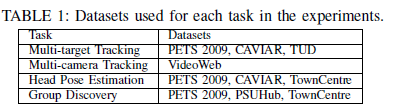
图1:(左图)社会群体行为不仅普遍存在与一个场景中,并且通常持续存在在广阔的区域中(有着相同的群体成员)。(右图)仅就头部图像而言,有时候人们很难在具有挑战性的场景中正确识别头部姿势的方向。社会环境为解决这类困难问题提供了强有力的支持。
我们介绍的社会群体信息是一类上下文信息。社会学研究显示,在自然环境中,70%的人会成群行走,它们的轨迹、速度和目的地是相似的。这些因素有助于消除在单相机(相似的轨迹和速度)和多相机追踪(相似的目的地)中令人困惑的追踪决策分歧。例如,在多相机追踪中,追踪器经常很难决定是去统一或者分离两个识别目标(即判断这两个识别目标是否是同一个),因为一个人在两个相机中通常看起来是很不一样的。然而,如果两个识别目标都有另一个相同的人陪同,那么将他们统一是首选的。直观清晰地规则是,如果是来自于一个群体中的人,他们头部的方向是相关联的,例如他们在看彼此又或者他们在看同一个地方。
在我们的工作中,我们提出了一个利用了社会群体信息的有效的概率框架用于视觉追踪和头部姿势评估。将追踪和社会群体的联合优化问题建模为约束非线性优化问题,这导致将部分涉及到标准快速程序(which results in steps involving standard fast procedures)。在群体中的头部姿势评估用条件随机场(CRF)建模为图形标注问题,这允许基于社会学研究的支持进行精确图学习和推理。我们的社会群体模型的通用性使得它适用于大多数现有的追踪连接和头部姿势识别框架。
我们的实验表明,社会上下文能够在现实世界数据集中帮助多目标追踪和头部姿势评估任务。特别感兴趣的,社会群体为单相机多目标追踪提供了一个自然的高阶关联,而当前存在的方法通常是依赖于复杂的解决方案去综合单阶间的关联(to go beyond single-order association)。更进一步,社会群体也是一整个系统的一个输出。我们的模型在基准数据集上得到的三个任务(追踪、头部姿势评估和社会群体发现)的结果比最先进的方法相近或者更好(见于表1),虽然我们的模型只应用了简单的运动和视觉特征。
本次工作的前期工作描述了社会群体与单相机和多相机追踪的关联。在本文中,我们也包含了头部姿势识别并且提出了一个统一观点。此外,我们还提供了更加全面的实验结果,包括了发现群体的性能评估。
2 - RELATD WORK
头部姿势评估、群体发现、特别是多目标追踪,已经在计算机视觉社区中被广泛研究。我们关注于那些与我们工作最相关的研究工作。
Single-camera multi-target tracking 多目标追踪是许多计算机视觉任务中关键的一步,包括视觉监视、活动识别以及场景的理解。实时性要求较强的方法通常使用粒子过滤算法进行状态的评估。然而,这类系统很难处理长期闭塞以及检测故障。因此,最近,基于数据关联的追踪(DAT,也称为追踪-连接问题)主导了该研究领域。在前沿的追踪提取方法(例如人类检测器方法)的帮助下,研究者观察到了延长时间区间并且连接保守提取的轨迹(短轨迹)以恢复完整的轨迹。许多人关注于如何获得更加可靠的轨迹连接概率。为了有效地推断出给定轨迹间的最佳匹配,研究者提出了不同的优化方法,例如Hungarian algorithm, K-shortest path, MWIS, set-cover, min-cost flow, approximate dynamic programming, continuous energy minimization等方法。重要地是,这些方法大多是order-one方法,这意味着它们只优化两两相似的点。这可能会导致全局的不一致性。一个典型的问题是图2中描述的运动依赖问题。
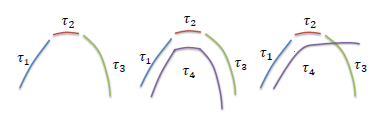
图2:(左图)order-one联系方法中的运动依赖问题:虽然τ1—τ2和τ2—τ3在理论上能够两两相连,但是却不可能得到完整的轨迹。(中图以及右图)τ4的社会群体信息有效的消除了轨迹间的依赖性,表明τ1—τ2—τ3是可能的(中图)而不是(右图)。
Yang等人应用CRF模型去减轻单一追踪的运动依赖问题。Butt以及Collins使用了对最小成本网络流框架的放松去探索更高阶的平滑约束,比如匀速。这些模型涉及到了复杂的解决方法并且仍然有局限性,因为它们只解决单一轨道的运动依赖问题:如图2所示,一个轨道突然改变运动的可能性可能取决于它是否有一个具有相似轨迹的群体成员。我们的模型,在另一方面,通过设计来建模这样的场景,可以建立在简单的求解器上,并且在与社会群体信息结合是可以自然的帮助高阶追踪(建模为全局时空聚类过程)。
Multi-camera multi-target tracking 多相机系统是无处不在的,一个可靠的多相机追踪系统允许广泛领域场景理解。研究者通常利用时空和外观线索在摄像机之间定位某一个目标。对于时空信息,Javed等人使用了一种Parzen窗口密度评估器去联合建模相机间的轨迹时间间隔、出入口位置以及目标速度。Makris等人提出了一种无监督学习方法去验证相机网络模型。在外观相似度方面,Javed等人展示了Brightness Transfer Function (BTF) 在应用于两个安置在低维度子空间下的相机并且提出了一种方法去学习它们间的标注对应关系。cumulative brightness transfer function (CBTF) 方法由Prosser等人提出,用于基于系数的训练集来实现相机间的颜色映射。Kuo等人使用Multiple Instance Learning (MIL) 来在线学习一种判别外观亲和度的模型(to learn a discriminative appearance affinity model online)。Orazio等人的工作评估了几个BTF方法并且发现它们表现出了相似的行为和局限性。我们的工作,在另一方面上,是第一个在多相机追踪问题中去探索社会群体信息,这将使得相机的特征(characteristics)、视觉点(viewpoints)以及关照条件变得更好。
Head pose estimation 头部姿势和目光方向评估是计算机领域和人类计算机交互(HCI)的一个长期研究领域。它使得各种各样的应用,例如人类注意力追踪和区域或焦点对象检测成为可能。大多数工作关注于头部图像分类,其中的图像具有合理的分辨率并且面部定位是可见的。Murphy-Chutorian和Trivedi给出了对此问题的各种不同方法的优秀综述。最近在该领域上取得进步包括了使用基于部分的模型。在我们的工作中,我们关注于在常见的高角度监控视频下的头部姿势评估,也称为头部方向和粗糙目光方向评估系统。相比于传统的姿势评估工作,头部图像的视觉特征因为数量规模小而通常很缺失,因此,对于人脸定位的方法是不适用的。这个问题通常被建模为回归问题(虽然因为在实际角度上处理离散标签是容易的,因此离散的类别有时作为中间的步骤。我们的工作采用了这种方法),这使得标注和预测的角度是不一样的,由于类标注的困难以及在特征空间中相近类别/角度具有相似性,因此我们并没有采用分类准确度来度量。大部分工作仍然关注于只基于头部图像本身采用特征提取和评估:Robertson和Rid探索了皮肤颜色特征。Tosato等人探索了协方差特征。histogram of gradient (HoG) 方法最近很受欢迎。Support Vector Machine (SVM),SVM Regressor, Neural Networks, Decision Trees, 以及Nearest Neighbor classifiers等分类和回归方法都在该领域得到了应用。最近的代表工作是由Benfold和Reid提出的结构化学习(structured leaning),提出了一种用于头像姿势评估的CRF。Chamveha等人提出了用于场景适应的光谱聚类。Chen和Odobez综合头部方向评估和身体姿势于一个通用核学习架构(a general kernel learning framework)。然而,全部已经存在的工作都只考虑个人。我们考虑了一般的社会行为倾向并且排除了特殊个体(general social tendency and repellence beyond individuals)。
Group discovery 社会群体发现最近在计算机视觉领域吸引了很多的关注。Ge等人根据追踪结果推断出社会群体。相比之下,我们同时进行分组和追踪。Chamveha等人使用了注意提示(attention cue)去帮助发现社会群体,而社会我们是先进行社会群体聚合然后用于帮助头部姿势评估。这是因为我们发现在具有挑战性的场景,头部姿势评估相比于社会群体发现会更加困难(Ge等人也注意到仅轨迹信息就足够用来实现分组任务)。
Socially-aware computer vision 社会上下文也成为几个计算机视觉问题探索的内容。对于追踪,Pirsiavash等人提出了一种基于社会信息更加有效的动态模型,Pirsiavash等人和Yamaguchi等人分别推断出社会群体可以得到更好的轨迹预测和更好的行为预测。Bazzani等人关注于追踪群体,Chen等人考虑当地群体的一致性。我们的工作是第一个在基于数据标注的多目标追踪和头部姿势评估问题中考虑社会群体上下文信息。
3 - SOCIAL GROUPING FOR MULTI-TARGET TRACKING AND HEAD POSE ESTIMATION
我们首先介绍我们基于社会群体信息的用于多目标跟踪和头部姿势评估的两个极大后验问题(MAP)的符号和概率公式。
3.1 - Notation
我们系统的输入是一组在时间间隔$[0,T]$中的$n$条轨迹的集合(可能包括假的信息)$\tau=\{\tau_1,\tau_2,...,\tau_n\}$,提取的方法描述见于6.2部分。每一条轨迹$\tau_i$是时间间隔$[t_i^{start},t_i^{finish}]$内对单个目标的简短描述序列。这些描述包括了目标的位置和大小(对于追踪问题),以及行人头部的位置和大小(对于头部姿势评估问题)。特别地,对于时刻$t$时的轨迹$\tau_i$,我们用$a_i(i)$表示标签(相机标签是离散的),$l_i(t)$表示位置(图片中的离散像素坐标)。我们假设$l_i(t)$同时表示了行人和头部的位置。
多目标追踪的任务时去识别出哪一条轨迹是与某一个目标有关联的,这可以用一个二值关系矩阵$\phi$表示:
$$\phi_{i,j}=\begin{cases} 1\ if\ tracklet\ j\ immediately\ follows\ tracklet\ i,\\ 0\ otherwise \end{cases}\ \ (1)$$
上式子添加约束条件$\Sigma_j\phi_{i,j}=1$和$\Sigma_i\phi_{i,j}=1$,这表明每一条轨迹只能与有且仅有一条轨迹相关联(除了最开始和最末尾的轨迹,这个问题在4.4.1部分采用虚拟开始和结束轨迹得以解决)。我们用$\Phi$表示有效的关联矩阵集合。
对于社会群体评估,我们将其建模为聚类问题并且假设人们来自于$K$个群体(其中$K$是未知的)。在每一个群体内部,有一条群体平均轨迹(一个图片坐标序列)$G_k$,表示为$G=\{G_1,G_2,...,G_K\}$。$\psi$用来表示一个二值社会群体分配矩阵:
$$\psi_{i,k}=\begin{cases} 1\ if\ tracklet\ i\ is\ assigned\ to\ group\ k,\\ 0\ otherwise \end{cases}\ \ (2)$$
这里又有一个约束$\Sigma_k\psi_{i,k}=1$并且我们使用$\Psi$来表示有效社会群体矩阵集合。
对于群体头部姿势评估,我们将在每一个时间点独立处理每一个群体,所以我们在这里丢弃了时间戳信息。用$C$表示群体中独立个体的数量,$Y$表示群体中每一个人的头部方向,$\Upsilon$表示在这个场景下所有头部图片的头部方向,$X$表示存在的一些个体一元证据(denote any existing unary evidence for individuals)(例如图像值或者行走方向;那有$M$种这样的特征),$L$表示行人头部的坐标。使用$y_j$和$l_j$表示第$j$个人的头部方向和坐标,$x_j^i$表示第$j$个人的第$i$个一元证据。因此有$Y=\{y_1,...,y_C\},L=\{l1,...,l_C\},X^i=\{x_1^i,...,x_C^i\}$,并且$X=\{X^1,...,X^M\}$。$X$和$L$的信息能够从轨迹描述中提取出来。
3.2 - The Probabilistic Model Formulation
对于给定输入的追踪、群体发现以及头部姿势评估的推理问题能够将其建模成两个极大后验问题(MAP):
$$(\phi^*,\psi^*,G^*)=\mathop{argmax}\limits_{\phi\in\Phi,\psi\in\Psi,G}\ P(\phi,\psi,G|\tau)\ \ (3)$$
以及
$$\Upsilon^*=\mathop{argmax}\limits_{\Upsilon}\ P(\Upsilon|\phi,\psi,G,\tau)\ \ (4)$$
在我们的工作中,第一个问题的输出是第二个问题的输入。因此对于这两个步骤采用一个简单的正向过滤器就可以得到所有所需的输出(追踪、群体发现、头部姿势评估)。
4 - COUPLING SOCIAL GROUPING WITH MULTI-TARGET TRACKING
我们对第一个MAP问题进行建模,有$P(\phi,\psi,G|\tau)$如下公式
$$\begin{align*}P(\phi,\psi,G|\tau)&\propto P(\phi,\psi,G,\tau) \\&=P(G)P(\tau,\psi|G)P(\phi|\tau,\psi,G)\\&=P(G)P(\tau,\psi|G)P(\phi|\tau,\psi)\end{align*}\ \ (5)$$
假设群体的轨迹与给定群体的轨迹连接互不影响。接下来我们将解释这个模型的每一个部分并且优化算法。
4.1 - Social Grouping as K-means Clustering
$P(\tau,\psi|G)$是对于类似K-means聚类的聚类算法的数据似然函数的概率解释。我们有
$$P(\tau,\psi|G)\propto\mathop{\Pi}\limits_{i,k|\psi_{ik}=1}P(\tau_i|G_k)\ \ (6)$$
假设对于每一个个体的轨迹与其他的群体平均轨迹是相互独立的(在general K-means聚类中也有相似的假设)。$P(\tau_i|G_k)$是群体$k$中的第$i$条轨迹的似然,其可根据时间分解成:
$$P(\tau_i|G_k)=\mathop{\Pi}\limits_{t=t_i^{start}}^{t_i^{finish}}P(a_i(t)|G_k)P(l_i(t)|a_i(t),G_k)\ \ (7)$$
$P(a_i(t)|G_k)$是群体$k$出现在相机$a_i(t)$的概率,这是模型中对于群体$k$的一个参数,我们将其表示为$b_{k,a}(t)$。$P(l_i(t)|a_i(t),G_k)$是在时间$t$的概率,在相机$a_i(t)$中出现的群体个体的坐标为$l_i(t)$,我们将其建模成一个以$u_{k,a}(t)$为中心的高斯模型,在时刻$t$群体$k$出现在相机$a$中的坐标也是模型对于群体$k$的一个参数。我们对于所有高斯模型用固定的方差。
注意到,这里我们为多相机场景提供了一个一般形式的公式。当在单相机情景下时,上面公式能够变得更加简单($P(a_i(t)|G_k)$能够被丢弃)。
4.2 - Socially Constrained Multi-target Tracking
$P(\phi|\tau,\psi)$根据社会群体信息来衡量轨迹连接的概率(或者多相机间的追踪切换)。与传统的追踪方法相比,这个方法在两条轨迹可以连接的时候加入了一个群体约束(表明这两条轨迹来自于同一个人),他们属于同一个群体(一组人均 one group per person):
$$P(\phi|\tau,\psi)=\mathop{\Pi}\limits_{i|\forall m,\phi_{m,i}}P_{init}(\tau_i)\mathop{\Pi}\limits_{j|\forall m,\phi_{j,m}}P_{term}(\tau_j)\times \mathop{\Pi}\limits_{i,j|\phi_{i,j}=1}\begin{cases}P_{link}(i,j)\ if\ \forall k,\psi_{i,k}=\psi_{j,k}\\0\ otherwise \end{cases}\ \ (8)$$
其中$P_init(\tau_i)$是当$\tau_i$为初始轨迹的似然概率,$P_term(\tau_j)$是当$\tau_j$为终止轨迹的似然概率。$P_{link}(i,j)$是轨迹$j$是轨迹$i$的第一个跟随实例的似然概率。这些概率是亲和模型的(the affinity model);任何来自文献的标准都可以使用(见于6.3部分)。
4.3 - A Simple Social Group Model
我们对于社会群体建立概率模型为
$$P(G)\propto e^{-\kappa|G|}\ \ (9)$$
用来惩罚有个体数量很多的社会群体,从而来避免过拟合(类似于把每一个人放到单独的一个小组里面)。注意到其他启发式方法也适用。我们的选择是直观的,在优化空间中得到了简单的线性惩罚,这在实验中验证了其有效性。
4.4 - Joint Optimization of Social Grouping and Multi-target Tracking
这个部分介绍了综合追踪和社会群体($P(G),P(\tau,\psi|G),and\ P(\phi|\tau,\psi)\ in\ Eq.\ 5$)为一个非线性约束优化框架,我们将其称为$SGB$(Social Grouping Behavior)算法。
我们首先在负对数空间中重新构建了社会群体和多目标追踪的联合优化并且提出了简介的公式。然后我们介绍了一种有效的优化框架,其可以应用于简单的现有方法(that can result in simple existing methods)。
4.4.1 Optimization Reformulation
我们在负指数似然空间重构了追踪和社会群体分组的联合优化(一个最小化问题)。忽略Eq.9中的比如系数。
$$-ln\ P(G)=\kappa |G|\ \ (10)$$
这个术语(this term)作为选择群体的数量,从而作为优化外层的循环。忽略掉$P(\tau,\psi|G)\ (Eq.6)$中一个类似的额外参数,我们可以从Eq.7中得到式子:
$$-ln\,P(\tau,\psi|G)=\sum_{i,k|\psi_{ik}=1}D(\tau_i,G_k)=\sum_{i,k|\psi_{ik}=1}\sum_{t=t_i^{start}}^{t_i^{finish}}-\alpha ln\,b_{k,a_i(t)}(t)+\beta \begin{vmatrix}l_i(t)-u_{k,a_i(t)}(t)\end{vmatrix}^2\ \ (11)$$
其中$\alpha$和$\beta$是高斯分布方差相关的权重。为了方便,我们定义$D(\tau_i,G_k)$来表示轨迹$i$和群体$k$的上述距离。在单相机情况下,分布$b_{k,a}(t)$将被简化掉并且从式子中去除。
$P(\phi|\tau,\psi)\ (Eq.8)$能够通过定义一个$2n\times2n$的轨迹连接矩阵转换为分配问题:

其中$H_{i,j}^{link}=-ln\,P_{link}(i,j),\ H_{i,i}^{init}=-ln\, P_{init}(\tau_i), H_{i,i}^{term}=-ln\,P_{term}(\tau_i)$以及$infinity(-ln\,0)\ elsewhere$包括所有对角元素)。引入了虚拟轨迹来解决轨迹的初始和终止问题。如果有等式违反了连接轨迹必须在同一个社会群体中的约束的话,Eq.8将会赋值为0。因此,如果我们把加入约束:$\forall i,j,k\ \phi_{i,j}(\psi_{i,k}-\psi_{j,k})=0$,则结果等式可以由$H$重写为:
$$-ln\,P(\phi|\tau,\psi)=\sum_{i,j}\phi_{i,j}H_{i,j}\ \ (13)$$
我们的优化外层循环尝试不同数量的社会群体。在内层(优化$P(\tau,\psi|G)$以及$P(\phi|\tau,\psi)$,我们能够丢掉Eq.10并且最小化有上述约束的Eq.13和Eq.11的和:
$$\begin{matrix}\mathop{min}\limits_{\phi\in \Phi,\psi\in\Psi,G}\sum_{i,j}\phi_{i,j}H_{i,j}+\sum_{i,k}\psi_{i,k}D(\tau_i,G_k)\\s.t.\ \forall i,j,k\ \phi_{i,j}(\psi_{i,k}-\psi{j,k})=0 \end{matrix}\ (14)$$
我们将Eq.14成为原始问题。