POJ 1191 DP+DFS棋盘分割问题

题目大意：

Description

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)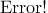原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。 均方差，其中平均值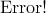，x_i为第i块矩形棋盘的总分。 请编程对给出的棋盘及n，求出O'的最小值。

 

运用动态规划，状态为int d(int k, int x1, int y1, int x2, int y2)，表示左上角为(x1, y1)，右下角为(x2, y2)的矩阵被切割成n块时可以达到的最小平方和。
状态转移方程为

nowstate=min( nowstate, dfs(k-1, x1, y1, a ,y2)+s[a+1, y1, x2, y2])

nowstate=min( nowstate, dfs(k-1, a+1, y1, x2, y2)+s[x1, y1, a, y2])

nowstate=min( nowstate, dfs(k-1, x1, b+1, x2, y2)+s[x1, y1, x2, b])

nowstate=min( nowstate, dfs(k-1, x1, y1, x2, b)+s[x1, b+1, x2, y2])

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
#define INF 0x3f3f3f3f
int dp[15][9][9][9][9],val[9][9],n;

int sum(int x1,int y1,int x2,int y2)
{
    int ans=val[x2][y2]-val[x1-1][y2]-val[x2][y1-1]+val[x1-1][y1-1];
    return ans*ans;
}

int dfs(int k,int x1,int y1,int x2,int y2)
{
    if(dp[k][x1][y1][x2][y2]) return dp[k][x1][y1][x2][y2];
    if(k==1||x1==x2||y1==y2){
        dp[k][x1][y1][x2][y2]= sum(x1,y1,x2,y2);
        return dp[k][x1][y1][x2][y2];
    }
    int nowstate=INF;
    for(int i=x1;i<x2;i++){
        nowstate=min(nowstate,dfs(k-1,i+1,y1,x2,y2)+sum(x1,y1,i,y2));
        nowstate=min(nowstate,dfs(k-1,x1,y1,i,y2)+sum(i+1,y1,x2,y2));
    }
    for(int i=y1;i<y2;i++){
        nowstate=min(nowstate,dfs(k-1,x1,i+1,x2,y2)+sum(x1,y1,x2,i));
        nowstate=min(nowstate,dfs(k-1,x1,y1,x2,i)+sum(x1,i+1,x2,y2));
    }
    dp[k][x1][y1][x2][y2]=nowstate;
    return nowstate;
}

void change()
{
    for(int i=0;i<=8;i++)
        val[i][0]=0,val[0][i]=0;

    for(int i=1;i<=8;i++)
        for(int j=1;j<=8;j++)
            val[i][j]+=val[i-1][j]+val[i][j-1]-val[i-1][j-1];
}

int main()
{
    while(~scanf("%d",&n)){

        memset(dp,0,sizeof(dp));

        for(int i=1;i<=8;i++)
            for(int j=1;j<=8;j++)
                scanf("%d",&val[i][j]);

        change();

        double res;
        double ave=1.0*val[8][8]/n;
        res=sqrt((double)dfs(n,1,1,8,8)/n-ave*ave);
        printf("%.3f
", res);
    }
    return 0;
}