一、算法说明
数据结构中经常需要用到各种排序算法,故参考网上代码,将九个排序算法整合在一起,以便日后使用。算法运行时,可以选择所要采用的排序算法,并会输出每一趟的排序过程,更利于对排序算法的理解。
二、运行截图
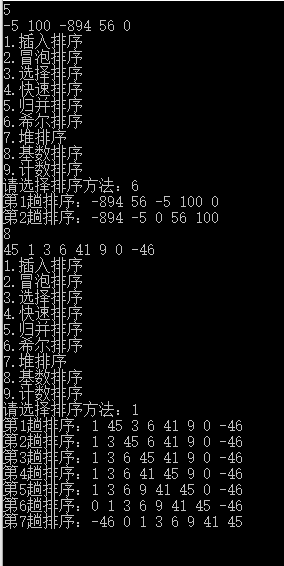
三、代码
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#define MAX_SIZE 100
int n, order, step;
int a[MAX_SIZE], temp[MAX_SIZE];
//输出排序情况
void print(int a[]);
//交换两个元素
void swap(int a[], int i, int j);
//插入排序
void Insert_sort(int a[], int size);
//冒泡排序
void Bubble_sort(int a[], int size);
//选择排序
void Selection_sort(int a[], int size);
//快速排序
void Quick_sort(int a[], int l, int r);
//归并排序
void Merge_sort(int a[], int temp[], int l, int r);
//希尔排序
void Shell_sort(int a[], int size);
//堆排序
void Heap_sort(int a[], int size);
//基数排序
void Radix_sort(int a[], int size);
//计数排序
void Count_sort(int a[], int temp[], int k, int size);
int main() {
while (~scanf("%d", &n)) {
step = 0;
for (int i = 0; i < n; i ++) {
scanf("%d", &a[i]);
}
printf("1.插入排序
2.冒泡排序
3.选择排序
4.快速排序
5.归并排序
6.希尔排序
7.堆排序
8.基数排序
9.计数排序
");
printf("请选择排序方法:");
scanf("%d", &order);
switch(order) {
case 1: {
Insert_sort(a, n);
break;
}
case 2: {
Bubble_sort(a, n);
break;
}
case 3: {
Selection_sort(a, n);
break;
}
case 4: {
Quick_sort(a, 0, n - 1);
break;
}
case 5: {
Merge_sort(a, temp, 0, n - 1);
break;
}
case 6: {
Shell_sort(a, n);
break;
}
case 7: {
Heap_sort(a, n);
break;
}
case 8: {
Radix_sort(a, n);
break;
}
case 9: {
Count_sort(a, temp, 9999, n);
break;
}
default: {
break;
}
}
}
return 0;
}
//输出排序情况
void print(int a[]) {
printf("第%d趟排序:", ++ step);
for (int i = 0; i < n; i ++) {
printf("%d ", a[i]);
}
printf("
");
}
//交换两个元素
void swap(int a[], int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
//插入排序
void Insert_sort(int a[], int size) {
for (int i = 1; i < size; i ++) {
int temp = a[i];
int j = i - 1;
while (j >= 0 && temp < a[j]) {
a[j + 1] = a[j];
j --;
}
a[j + 1] = temp;
print(a);
}
}
//冒泡排序
void Bubble_sort(int a[], int size) {
for (int j = 0; j < size - 1; j++) {
for (int i = 0; i < size - 1 - j; i++) {
if (a[i] > a[i + 1]) {
swap(a, i, i + 1);
}
}
print(a);
}
}
//选择排序
void Selection_sort(int a[], int size) {
for (int i = 0; i < size - 1; i ++) {
int min = i;
for (int j = i + 1; j < size; j ++) {
if (a[j] < a[min]) {
min = j;
}
}
if (min != i) {
swap(a, min, i);
}
print(a);
}
}
//快速排序
void Quick_sort(int a[], int l, int r) {
if (l < r) {
int i = l, j = r, x = a[l];
while (i < j) {
while(i < j && a[j] >= x)
j --;
if(i < j)
a[i ++] = a[j];
while(i < j && a[i] < x)
i ++;
if(i < j)
a[j --] = a[i];
}
a[i] = x;
print(a);
Quick_sort(a, l, i - 1);
Quick_sort(a, i + 1, r);
}
}
//归并排序:合并操作
void Merge(int a[], int temp[], int l, int mid, int r) {
int i = l, j = mid + 1, k = l;
while(i != mid + 1 && j != r+1) {
if(a[i] < a[j])
temp[k ++] = a[i ++];
else
temp[k ++] = a[j ++];
}
while(i != mid + 1)
temp[k ++] = a[i ++];
while(j != r + 1)
temp[k ++] = a[j ++];
for(i = l; i <= r; i ++)
a[i] = temp[i];
print(a);
}
//归并排序
void Merge_sort(int a[], int temp[], int l, int r) {
if(l < r) {
int mid = (l + r) / 2;
Merge_sort(a, temp, l, mid);
Merge_sort(a, temp, mid + 1, r);
Merge(a, temp, l, mid, r);
}
}
//希尔排序
void Shell_sort(int a[], int size) {
for (int gap = n / 2; gap > 0; gap /= 2) {
for (int i = 0; i < gap; i++) {
for (int j = i + gap; j < n; j += gap) {
if (a[j] < a[j - gap]) {
int temp = a[j];
int k = j - gap;
while (k >= 0 && a[k] > temp) {
a[k + gap] = a[k];
k -= gap;
}
a[k + gap] = temp;
}
}
}
print(a);
}
}
//堆排序:从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
void HeapAdjust(int a[], int i, int n) {
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n) {
if (j + 1 < n && a[j + 1] > a[j]) //在左右孩子中找最大的
j++;
if (a[j] <= temp)
break;
a[i] = a[j]; //把较大的子结点往上移动,替换它的父结点
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}
//堆排序:建立最大堆
void BuildHeap(int a[], int n) {
for (int i = n / 2 - 1; i >= 0; i--)
HeapAdjust(a, i, n);
}
//堆排序
void Heap_sort(int a[], int size) {
BuildHeap(a, size);
for (int i = n - 1; i >= 1; i--) {
swap(a, i, 0);
HeapAdjust(a, 0, i);
print(a);
}
}
//基数排序
void Radix_sort(int a[], int size) {
int *radixArrays[10];
for (int i = 0; i < 10; i++) {
radixArrays[i] = (int *)malloc((size + 1) * sizeof(int));
radixArrays[i][0] = 0;
}
for (int pos = 0; pos < 10; pos ++) {
int ok = 0; //最大元素是否已经排序完毕
for (int i = 0; i < size; i ++) {
int num = (a[i] / (int) pow(10, pos)) % 10; //num为每个元素个位、十位、百位。。。等的数字
if (num == 0) ok ++;
int index = ++ radixArrays[num][0]; //index为每个桶的元素个数
radixArrays[num][index] = a[i];
}
if (ok == size) break;
//收集过程
for (int i = 0, j = 0; i < 10; i ++) {
for (int k = 1; k <= radixArrays[i][0]; k++)
a[j++] = radixArrays[i][k];
radixArrays[i][0] = 0;
}
print(a);
}
}
//计数排序
void Count_sort(int a[], int temp[], int k, int size) {
// a为输入数组,temp为输出数组,k表示有所输入数字都介于0到k之间
int c[k];
// 初始化
for (int i = 0; i < k; i++) {
c[i] = 0;
}
// 检查每个输入元素,如果一个输入元素的值为a[i],那么c[a[i]]的值加1,此操作完成后,c[i]中存放了值为i的元素的个数
for (int i = 0; i < n; i++) {
c[a[i]]++;
}
// 通过在c中记录计数和,c[i]中存放的是小于等于i元素的数字个数
for (int i = 1; i < k; i++) {
c[i] = c[i] + c[i - 1];
}
// 把输入数组中的元素放在输出数组中对应的位置上
for (int i = n - 1; i >= 0; i--) {// 从后往前遍历
temp[c[a[i]] - 1] = a[i];
c[a[i]]--;// 该操作使得下一个值为a[i]的元素直接进入输出数组中a[i]的前一个位置
}
for (int i = 0; i < n; i ++) {
a[i] = temp[i];
}
print(a);
}