Author : Houge
Problem set : Codeforces Beta Round #2
A - Winner
题目大意:
进行n轮游戏,每一轮以“名字 分数”的形式输入,第一个到达最高分的人为胜利者。
分析:
简单的模拟,可以用map储存姓名和分数,模拟两遍,第一遍先求出最高分,第二遍求出第一个到达最高分的人。(注意:分数可能有负数)
代码:

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 map<string,int> mp; 6 map<string,int>::iterator it; 7 8 int main() 9 { 10 int n,m,score[1005],i,j,max=-999999; 11 string name[1005],ans,winnerlist[1005]; 12 cin>>n; 13 for(i=0;i<n;i++) 14 { 15 cin>>name[i]>>score[i]; 16 mp[name[i]]+=score[i]; 17 } 18 for(it=mp.begin();it!=mp.end();it++) 19 { 20 if(it->second>max) 21 { 22 ans=it->first; 23 max=it->second; 24 } 25 } 26 m=0; 27 for(it=mp.begin();it!=mp.end();it++) 28 if(it->second==max) winnerlist[m++]=it->first; 29 mp.clear(); 30 j=m; 31 for(i=0;i<n;i++) 32 { 33 mp[name[i]]+=score[i]; 34 if(mp[name[i]]>=max) 35 { 36 for(m=0;m<j;m++) 37 if(name[i]==winnerlist[m]) 38 { 39 ans=name[i]; 40 goto AN; 41 } 42 } 43 } 44 AN: 45 cout<<ans; 46 return 0; 47 }
B - The least round way
题目大意:
给你一个由非负整数组成的矩阵,让你从左上走到右下,每次只能向左或者向下走。最后将路径上的数字相乘,问你怎么走才能使最后相乘结果中末尾的0的个数最少。输出0的个数和走的路线。
分析:
dp,我们知道,几个数相乘,最后结果末尾的0的个数只和因子2和因子5的个数相关,想要得到最少的0,就要是路径中的因子2和因子5的数量尽量少。我们来思考以下几点:
·同时对因子2和因子5进行状态转移是不方便的,我们不如将它们两个的状态转移分开进行,最后取个数最小的作为结果即可。那么我们定义数组dp[i][j][0/1]来存储到(i,j)点时,因子2/因子5的最少个数,dp数组的初值为(i,j)点本身的因子2个数和因子5个数。
·对于每一步的下一个操作,我们都有两种方案:向下移动和向右移动,即对于(i,j)只能是从(i-1,j)或(i,j-1)转移过来。我们要取所求因子数较少的方案作为决策。这样即可得出状态转移方程:
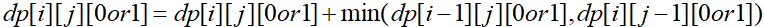
·需要考虑几种特判情况:起点(0,0),i=0(没有上一行)和j=0(没有左一列),路径中有0的情况(不论怎么走,0的个数都是1)。
对于以上三种情况可以如下解决:①起点直接continue②i=0和j=0时单独处理(遍历时从1开始也可)③如在矩阵中出现0,记录下位置,输出时特殊处理。
·如何记录路径:
对于路径的记录,我们可以用pre[i][j][0/1][x/y]数组记录(i,j)点的上一个点的坐标,用order[i][j][0/1]字符数组记录(i,j)点是由何操作得到的(均要分因子2和因子5的情况)。最后根据pre数组倒着遍历路径,将order存入栈中实现先进后出。
代码:

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=1005; 6 int matrix,dp[MAXN][MAXN][2],pre[MAXN][MAXN][2][2]; //dp[i][j][0/1]分别存储到(i,j)点时,因子2/因子5的最少个数;pre[i][j][0/1][x/y]表示(i,j)点在因子2/因子5的情况下上一个点的坐标 7 char order[MAXN][MAXN][2]; //order[][][0/1]储存因子2/因子5的情况下对应的操作(R/D) 8 9 int main() 10 { 11 int i,j,n,flag=0,mingcd,temp,tx,ty; 12 scanf("%d",&n); 13 for(i=0;i<n;i++) 14 for(j=0;j<n;j++) //输入,并做初步处理:1.算出因子2和因子5的数量并存入dp数组 2.找到0存储坐标准备特判 15 { 16 scanf("%d",&matrix); 17 if(matrix==0) flag=1,dp[i][j][0]=1,dp[i][j][1]=1,tx=i,ty=j; 18 else 19 { 20 if(matrix%2==0) 21 { 22 temp=matrix; 23 while(temp%2==0) 24 { 25 dp[i][j][0]++; 26 temp/=2; 27 } 28 } 29 if(matrix%5==0) 30 { 31 temp=matrix; 32 while(temp%5==0) 33 { 34 dp[i][j][1]++; 35 temp/=5; 36 } 37 } 38 } 39 } 40 for(i=0;i<n;i++) //dp循环,因子2和因子5的情况要分开进行,(0,0),i=0,j=0三种特判。状态转移方程:(i,j)因子X数量=min((i-1,j)因子X数量,(i,j-1)因子X数量) 41 { 42 for(j=0;j<n;j++) 43 { 44 if(i==0&&j==0) continue; 45 if(i==0) 46 { 47 dp[i][j][0]+=dp[i][j-1][0]; 48 dp[i][j][1]+=dp[i][j-1][1]; 49 order[i][j][0]='R',order[i][j][1]='R'; 50 pre[i][j][0][0]=i,pre[i][j][1][0]=i; 51 pre[i][j][0][1]=j-1,pre[i][j][1][1]=j-1; 52 continue; 53 } 54 if(j==0) 55 { 56 dp[i][j][0]+=dp[i-1][j][0]; 57 dp[i][j][1]+=dp[i-1][j][1]; 58 order[i][j][0]='D',order[i][j][1]='D'; 59 pre[i][j][0][0]=i-1,pre[i][j][1][0]=i-1; 60 pre[i][j][0][1]=j,pre[i][j][1][1]=j; 61 continue; 62 } 63 if(dp[i-1][j][0]>dp[i][j-1][0]) 64 { 65 dp[i][j][0]+=dp[i][j-1][0]; 66 order[i][j][0]='R'; 67 pre[i][j][0][0]=i; 68 pre[i][j][0][1]=j-1; 69 } 70 else 71 { 72 dp[i][j][0]+=dp[i-1][j][0]; 73 order[i][j][0]='D'; 74 pre[i][j][0][0]=i-1; 75 pre[i][j][0][1]=j; 76 } 77 if(dp[i-1][j][1]>dp[i][j-1][1]) 78 { 79 dp[i][j][1]+=dp[i][j-1][1]; 80 order[i][j][1]='R'; 81 pre[i][j][1][0]=i; 82 pre[i][j][1][1]=j-1; 83 } 84 else 85 { 86 dp[i][j][1]+=dp[i-1][j][1]; 87 order[i][j][1]='D'; 88 pre[i][j][1][0]=i-1; 89 pre[i][j][1][1]=j; 90 } 91 } 92 } 93 if(dp[n-1][n-1][0]>dp[n-1][n-1][1]) 94 { 95 mingcd=dp[n-1][n-1][1]; 96 temp=1; 97 } 98 else 99 { 100 mingcd=dp[n-1][n-1][0]; 101 temp=0; 102 } 103 if(mingcd==0) flag=0; //如果有没有0的路径,则需取消特判 104 if(flag) //特判 105 { 106 printf("1 "); 107 int a1,a2,a3,a4; 108 a1=tx,a2=ty,a3=n-1-tx,a4=n-1-ty; 109 while(a1--) printf("D"); 110 while(a2--) printf("R"); 111 while(a3--) printf("D"); 112 while(a4--) printf("R"); 113 } 114 else //输出,用stack维护实现先进后出 115 { 116 printf("%d ",mingcd); 117 int x=n-1,y=n-1; 118 stack<char> opt; 119 while(x||y) 120 { 121 //cout<<"TEST1: "<<x<<' '<<y<<endl; 122 int mx,my; 123 opt.push(order[x][y][temp]); 124 mx=pre[x][y][temp][0]; 125 my=pre[x][y][temp][1]; 126 x=mx,y=my; 127 //cout<<"TEST2: "<<x<<' '<<y<<endl; 128 } 129 while(!opt.empty()) 130 { 131 cout<<opt.top(); 132 opt.pop(); 133 } 134 } 135 return 0; 136 }
C - Commentator problem
题目大意:
给你三个圆,找到一个点,使得这个点与三个圆分别构成的视角大小都一样。
分析:
计算几何,但如果真的用计算几何做,麻烦且不好理解。这题还可以用模拟退火来解,特意学习了下,大意就是拟定一个初始坐标,然后不断减少该点与正确点的误差,最后输出。分析打在注释里,详见代码。
代码:

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 struct point 6 { 7 double x,y,r; 8 }p[5]; 9 10 int judge[4][2]={-1,0,0,-1,1,0,0,1}; //调整点时使用 11 double angle[3]; 12 13 double dist(point a,point b) //求两点间距离 14 { 15 return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); 16 } 17 18 double error(point a) //求该点视角误差(方法唯一?) 19 { 20 int i; 21 for(i=0;i<3;i++) angle[i]=dist(a,p[i])/p[i].r; 22 double err=0; 23 for(i=0;i<3;i++) err+=(angle[i]-angle[(i+1)%3])*(angle[i]-angle[(i+1)%3]); 24 return err; 25 } 26 27 int main() 28 { 29 double ansx,ansy; 30 int i; 31 for(i=0;i<3;i++) cin>>p[i].x>>p[i].y>>p[i].r; 32 ansx=(p[0].x+p[1].x+p[2].x)/3; 33 ansy=(p[0].y+p[1].y+p[2].y)/3; //^^^^初始坐标 34 double err=error((point){ansx,ansy,0}); //初始误差 35 double step=1; 36 for(int T=1;T<=1e5;T++) //模拟退火,不断更新点的坐标 37 { 38 int flag=0; 39 double x,y; 40 for(i=0;i<4;i++) 41 { 42 double nx=ansx+judge[i][0]*step; 43 double ny=ansy+judge[i][1]*step; 44 double nerr=error((point){nx,ny,0}); //^^^^调整点,求新的误差 45 if(nerr<err) //误差变小,是更优解,更新坐标 46 { 47 err=nerr; 48 x=nx; 49 y=ny; 50 flag=1; 51 } 52 } 53 if(flag==0) step/=2; //更新坐标后缩小调整的幅度,逼近最优解 54 else ansx=x,ansy=y; 55 } 56 if(err<1e-6) printf("%.5f %.5f ",ansx,ansy); //答案在误差范围内就输出 57 return 0; 58 }
