数论又多又难,该从哪开始学呢?不如先思考一下下面这个问题:
对于一个自然数n,它的因数是什么?
一、因数的筛法
1.最简单的暴力
相信只要你有一点数学和编程基础的话,都会想到下面这个最简单暴力的方法:
1 int find_factor(int x) 2 { 3 int i,cnt=0; 4 for(i=1;i<=x;i++) 5 if(x%i==0) cnt++; 6 return cnt; 7 }
对,只要从1到n遍历一遍,看看是不是n的因数就解决了。但是这样的话有一个缺点,该算法的时间复杂度为O(n),数据稍微一大,就超时了。
2.修改后的筛法
那么我们能不能稍微改进一下这个算法呢?答案是可以的,我们都知道一个数的因数一定是成对出现的,那么对于每一组里小的那个因数,它的大小不会超过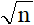 ,利用这一点我们可以将我们的算法做如下改进:
,利用这一点我们可以将我们的算法做如下改进:
我们可以用下面的代码实现分解质因数(时间复杂度O(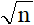 )):
)):
 分解质因数
分解质因数
1 int find_factor(int x) 2 { 3 int i,cnt=0; 4 for(i=1;i*i<=x;i++) 5 if(x%i==0) 6 { 7 if(i*i==x) cnt++; //当x=i*i时,计数器只需加一次 8 else cnt+=2; 9 } 10 return cnt; 11 }
这样一来,我们的时间复杂度就变为了O(![]() ),可以解决更大范围的数据了。上面的筛法也是在大多数题目中适用的。
),可以解决更大范围的数据了。上面的筛法也是在大多数题目中适用的。
3.加强版筛法
但是还是有更加善良的出题人,想要继续考察我们,这就需要我们学习专业的数学知识了。我们先来看下面两个概念:
·分解质因数:把n表示为质数相乘的形式,如30=2×3×5。我们可以用下面的代码实现分解质因数(时间复杂度O(

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 void resolved() 6 { 7 int i,n,temp; 8 scanf("%d",&n); 9 printf("%d=",n); 10 temp=n; 11 if(n<2) return ; //小于2的数不合法,若n为质数则输出它本身 12 for(i=2;i*i<=temp;i++) //根号n复杂度 13 while(temp%i==0) 14 { 15 temp=temp/i; 16 printf("%d",i); 17 if(temp!=1) printf("*"); 18 } 19 if(temp!=1) printf("%d",temp); //当n为质数 20 return ; 21 } 22 23 int main() 24 { 25 resolved(); 26 return 0; 27 }
(还有一个时间复杂度为O(![]() )的算法,日后再补)
)的算法,日后再补)
既然这些因数都是质数,我们可以把一个数n的分解质因数表示为:
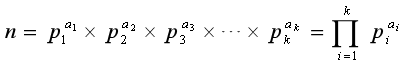
其中,p1、p2、p3…pk是由小到大的质数,如:36=2×2×3×3=22×32。
·约数个数定理:对于一个大于1正整数n可以分解质因数:

则n的正约数的个数就是:

其中a1、a2、a3…ak是p1、p2、p3…pk的指数。
感觉不太好理解?我们来看下面几个实例:
(1)10=2×5=21×51
10的因子:1(20×50),2(21×50),5(20×51),10(21×51),
因子的个数=4=(1+1)×(1+1);
(2)36=2×2×3×3=22×32
36的因子:1(20×30),2(21×30),4(22×30),3(20×31),6(21×31),12(22×31),9(20×32),18(21×32),36(22×32),
因子的个数=9=(2+1)×(2+1);
看完这几个例子,不知你感觉如何,接着我们用代码来实现这个过程:
1 int find_factor(int x) 2 { 3 int cnt=1,p=2; //p代表素数 4 while(x!=1) 5 { 6 int t=1; //t最终代表(a[i]+1) 7 while(x%p==0) 8 { 9 x=x/p; 10 t++; 11 } 12 p++; 13 cnt*=t; 14 } 15 return cnt; 16 }
这个方法不光可用用来求一个数的因数的个数,还可以用来解与因数个数相关的问题。
二、约数个数定理的应用
我们来看下面几个问题:
1.求1到n里面约数最多的数的约数个数(n<=1018)
这个题注意数据!!!一看到这个数据我们就知道暴力是不可能实现的,那么又如何使用上面的方法呢?如果用上面的方法进行枚举也是不可取的。
那么我们来简单分析下这个问题:
·我们知道每一个数都可以用质因子的积表示,而约数的个数只与指数有关!
这个题注意数据!!!一看到这个数据我们就知道暴力是不可能实现的,那么又如何使用上面的方法呢?如果用上面的方法进行枚举也是不可取的。
那么我们来简单分析下这个问题:
·我们知道每一个数都可以用质因子的积表示,而约数的个数只与指数有关!
·我们知道pn>...>p3>p2>p1,那么假设我们存在某一个ak>a1 那么我们交换pk与p1的指数,显然约数个数不变,但是数变小了!
如:24=23×31和54=21×33。
·也就是说对于任何n,m如果pn>pm那么an<am 要好一些。但是不是最优的,不确定,不过这已经为我们淘汰了许多不必要的情况了。这样使用dfs与之结合,枚举每一个质因子的质数,保证其指数递减,然后我们就可以写出代码了:
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 int prime[25]={1,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89}; //存一下质数 6 long long n,ans; 7 8 //pos代表第几个质数,num代表目前因子的个数,multi代表目前的数,len代表循环的次数 9 void get_num_dfs(int pos,long long num,long long multi,int len) 10 { 11 int i; 12 if(multi>n) return ; 13 if(multi<=n) ans=max(ans,num); 14 for(i=1;i<=len;i++) 15 { 16 long long temp=pow(prime[pos],i); 17 if(multi>n/temp) break; //用除法防止爆long long 18 get_num_dfs(pos+1,num*(i+1),multi*temp,i); //进行下一个状态 19 } 20 return ; 21 } 22 23 int main() 24 { 25 int t; 26 scanf("%d",&t); 27 while(t--) 28 { 29 ans=0; 30 scanf("%lld",&n); 31 get_num_dfs(1,1,1,64); 32 printf("%lld ",ans); 33 } 34 return 0; 35 }
Author : Houge Date : 2019.5.27
Update log :
2019.5.30:修正了一处错误。
