最小生成树MST

最小生成树(Minimum Spanning Trees)

Kruskal算法和Prim算法都是典型的贪心算法。

Kruskal

Kruskal算法的时间为：O(ElgE)。
➢ 如果再注意到|E|<|V|2，则有lg|E|=O(lgV )，所以Kruskal算法的时间可表示为O(ElgV)。
适合边数较少的情况。

//kruskal-->MST
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

typedef struct Edge {
	int src, dest, weight;
}Edge;

typedef struct Graph {
	int V, E;	//V: 总节点数  E: 总边数
	Edge* edge;
}Graph;

Graph* createGraph(int V, int E) {
	Graph* graph = new Graph;
	graph->V = V;
	graph->E = E;
	graph->edge = new Edge[E];

	return graph;
}
//union-find  并查集
typedef struct subset {
	int parent;
	int rank;	//子树深度，合并时用
}subset;

int find(subset subsets[], int i) {
	if (subsets[i].parent != i)
		subsets[i].parent = find(subsets, subsets[i].parent);
	return subsets[i].parent;
}
//合并 集合
void Union(subset subsets[], int x, int y) {
	int xroot = find(subsets, x);
	int yroot = find(subsets, y);

	if (subsets[xroot].rank < subsets[yroot].rank)
		subsets[xroot].parent = yroot;
	else if (subsets[xroot].rank > subsets[yroot].rank)
		subsets[yroot].parent = xroot;
	else {
		subsets[yroot].parent = xroot;
		subsets[xroot].rank++;
	}
}

int mycomp(const void* a, const void* b) {
	//	return ((Edge*)a)->weight > ((Edge*)b)->weight;
	return (*(Edge*)a).weight > (*(Edge*)b).weight;
}

/*
*边排序-> 遍历-> 符合条件加入
*/
void KruskalMST(Graph* graph) {
	int V = graph->V;
	Edge* result = (Edge*)malloc(V * sizeof(Edge));
	int e = 0;
	int i = 0;
	qsort(graph->edge, graph->E, sizeof(graph->edge[0]), mycomp);

	subset* subsets = (subset*)malloc(V * sizeof(subset));
	for (int v = 0; v < V; v++) {	//初始化V个并查集
		subsets[v].parent = v;
		subsets[v].rank = 0;
	}
	/*-------核心代码--------*/
	while (e < V - 1 && i < graph->E) {		//V个点，V-1条边
		Edge minEdge = graph->edge[i++];
		int x = find(subsets, minEdge.src);
		int y = find(subsets, minEdge.dest);

		if (x != y) {
			result[e++] = minEdge;
			Union(subsets, x, y);
		}
	}
	/*--------------------*/
	printf("edges in MST:
");
	int minCost = 0;
	for (i = 0; i < e; i++) {
		printf("%d ------ %d == %d
", result[i].src, result[i].dest, result[i].weight);
		minCost += result[i].weight;
	}
	printf("minCost: %d
", minCost);
	return;
}

int main() {
	//煮个栗子
	int V = 4;
	int E = 5;
	Graph* graph = createGraph(V, E);

	graph->edge[0].src = 0;
	graph->edge[0].dest = 1;
	graph->edge[0].weight = 10;

	graph->edge[1].src = 0;
	graph->edge[1].dest = 2;
	graph->edge[1].weight = 6;

	graph->edge[2].src = 0;
	graph->edge[2].dest = 3;
	graph->edge[2].weight = 5;

	graph->edge[3].src = 1;
	graph->edge[3].dest = 3;
	graph->edge[3].weight = 15;

	graph->edge[4].src = 2;
	graph->edge[4].dest = 3;
	graph->edge[4].weight = 4;

	KruskalMST(graph);
	return 0;
}

切割

无向图G=(V,E)的一个切割(S,V-S)是集合V的一个划分。

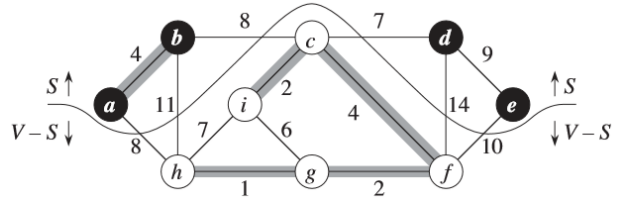
横跨切割

如果一条边(u,v)∈E的一个端点在集合S中，另一个端点在集合V-S中，则称该条边横跨切割(S,V-S)。

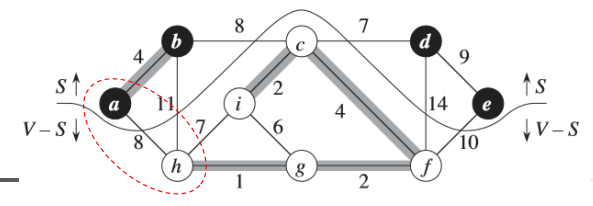
尊 重

如果边集A中不存在横跨该切割的边，则称该切割尊 重集合A。

轻量级边

在横跨一个切割的所有边中，权重最小的边称为轻量级边。
➢ 轻量级边可能不是唯一的。
➢ 一般，如果一条边是满足某个性质的所有边中权重最小的，则称该边是满足给定性质的一条轻量级边