20162314补分博客汇总

20162314补分博客汇总

课堂测试

• 1.Dijkstra

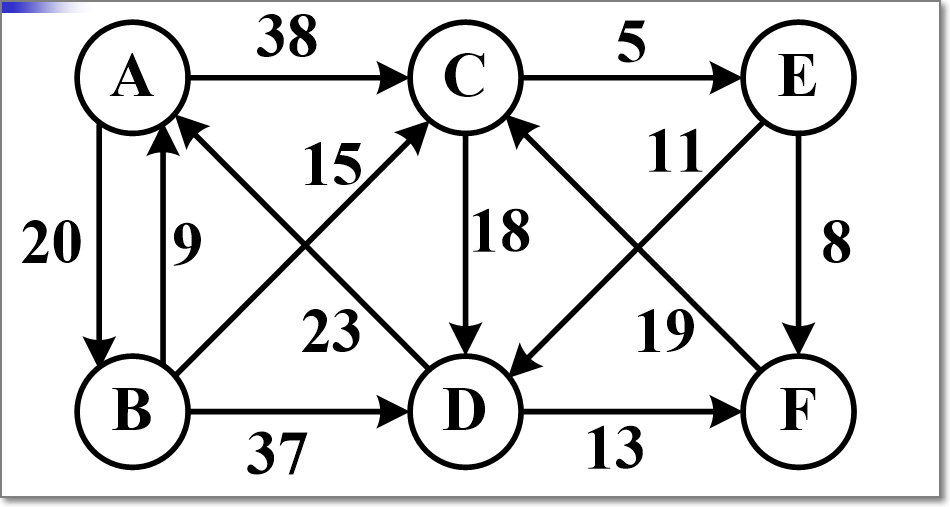
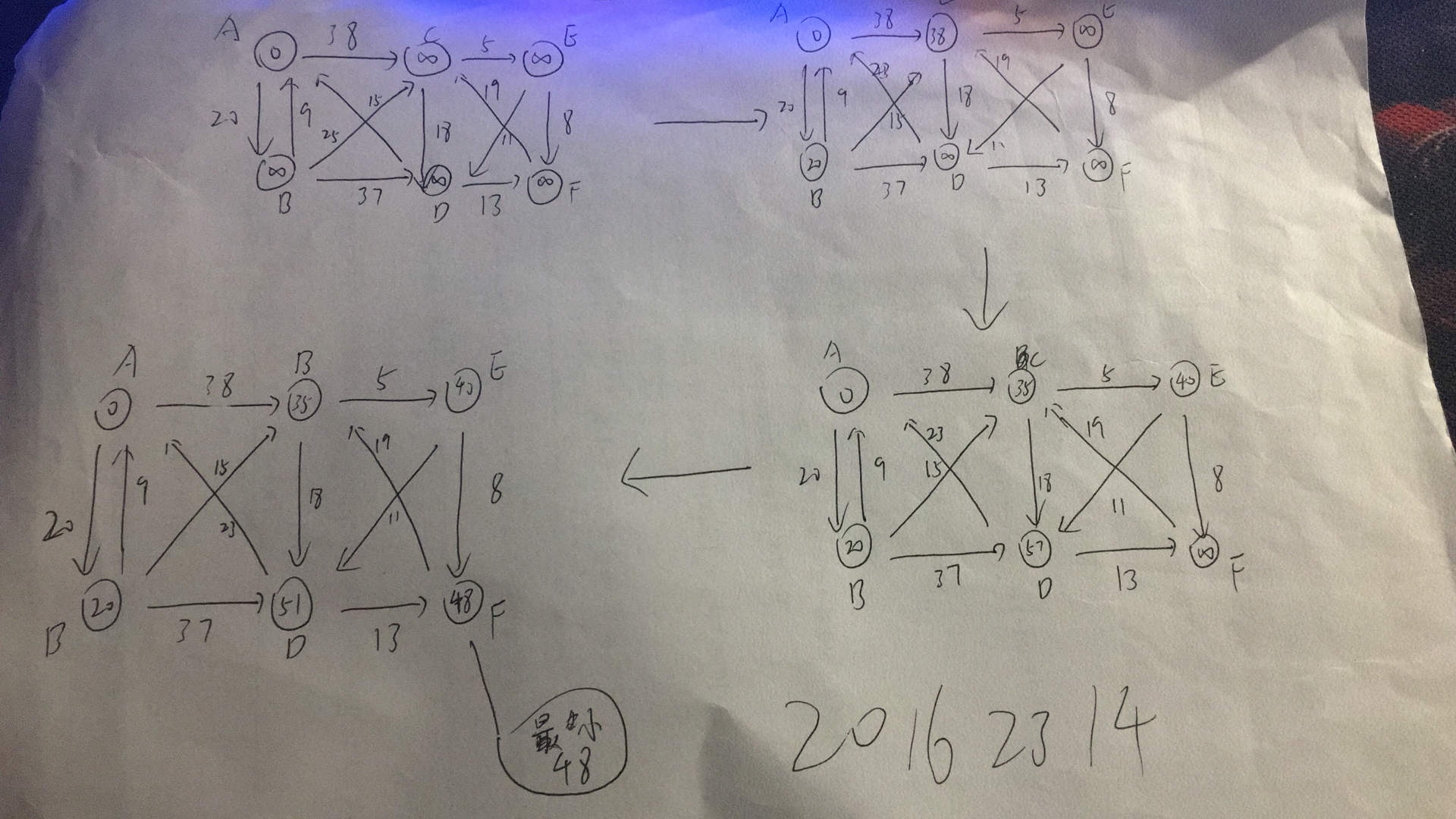
Dijkstra算法，求解附图顶点A的单源最短路径

S为已经找到的从v出发的最短路径的终点集合，它的初始状态为空集，那么从v出发到图中其余各顶点（终点）vi（vi∈V-S）可能达到的最短路径长度的初值为：
d[i] = arcs[LocateVex(G, v)][i]，vi∈V
最短：从A开始，选入A到B（20），B到C（15)，选入C到E（5），选入E到F（8），选入E到D（11），最短为48

• 2.最小生成树

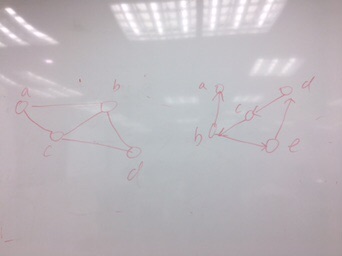
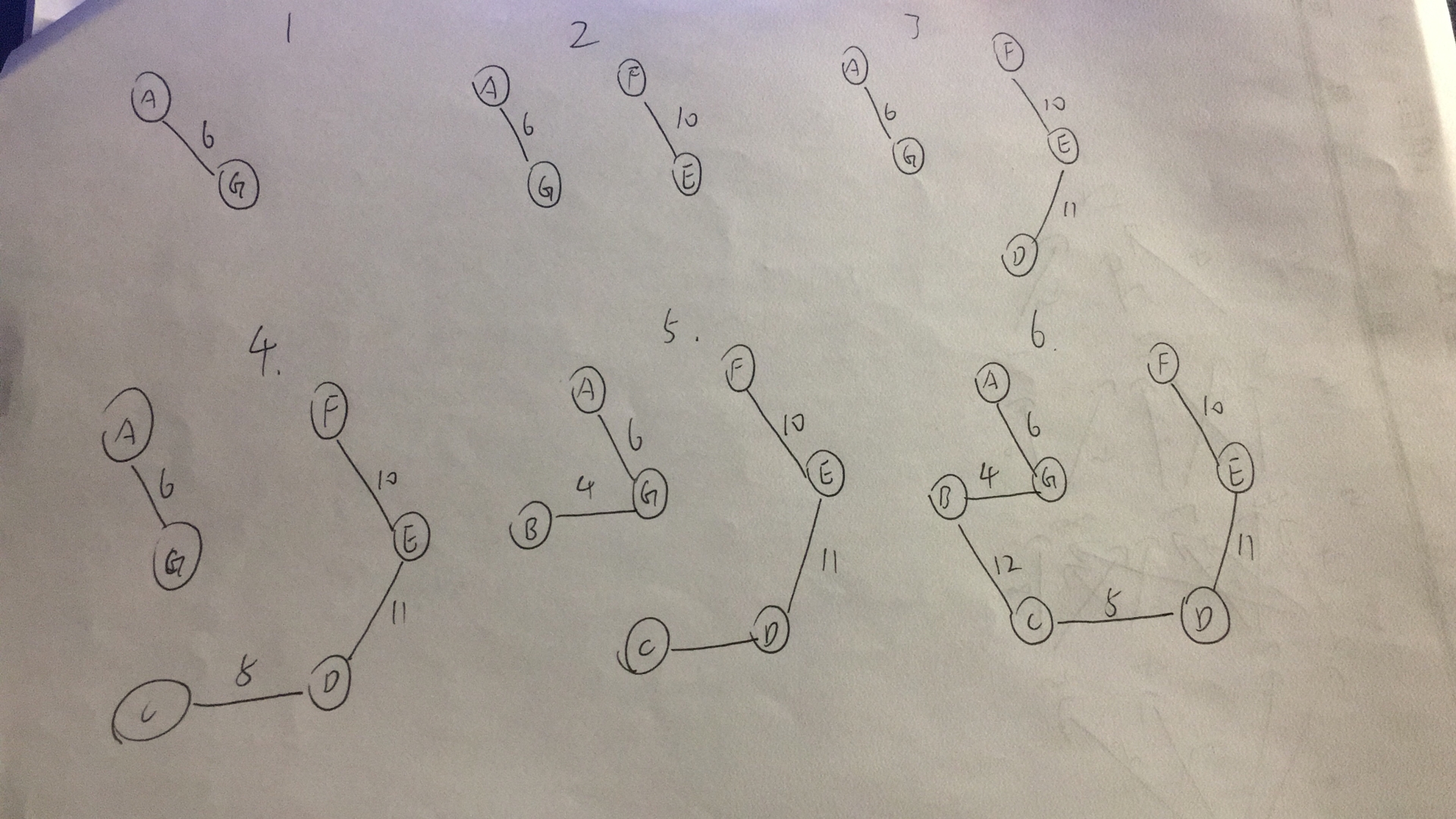
构造附图带权无向图的最小生成树，给出该最小生成树代价。说明Prim和Kruskal算法差别。

克鲁斯卡尔算法的执行步骤：
第一步：在带权连通图中，将边的权值排序；
第二步：判断是否需要选择这条边（此时图中的边已按权值从小到大排好序）。判断的依据是边的两个顶点是否已连通，如果连通则继续下一条；如果不连通，那么就选择使其连通。
第三步：循环第二步，直到图中所有的顶点都在同一个连通分量中，即得到最小生成树。

普利姆算法的核心步骤是：在带权连通图中，从图中某一顶点v开始，此时集合U={v}，重复执行下述操作：在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边，将(u,w)这条边加入到已找到边的集合，并且将点w加入到集合U中，当U=V时，就找到了这颗最小生> > 成树。
最小代价48，Prime从点入手--稠密图，Kruskal从边入手---稀疏图

• 3.图的广度优先遍历

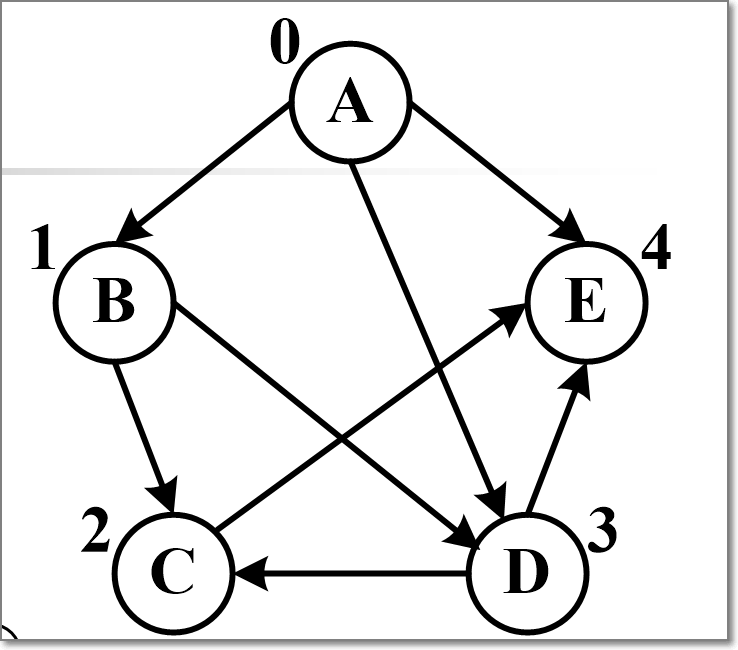
写出附图从每个顶点出发的一次广度优先搜索遍历序列。

广度优先搜索的基本思想是：

（1）从图中的某个顶点V出发，访问之；并将其访问标志置为已被访问，即visited[i]=1；

（2）依次访问顶点V的各个未被访问过的邻接 点，将V的全部邻接点都访问到；

（3）分别从这些邻接点出发，依次访问它们的未被访问过的邻接点，并使“先被访问的顶 点的邻接点”先于“后被访问的顶点的邻接点”被访问，直到图中所有已被访问过的顶 点的邻接点都被访问到。

依此类推，直到图中所有顶点都被访问完为止 。

A：A---BDE---C
B：B---CD---E
C：C---E
D：D---CE
E：E

• 4.图的深度优先遍历

写出附从每个顶点出发的一次深度优先搜索遍历序列。

深度优先遍历
具体步骤如下：
　　　　（1）初始化：将所有顶点置为未访问，其父亲结点均为-1

　　　　（2）遍历每一个顶点u，如果它未访问，则对该顶点进行（3）操作

　　　　（3）置该顶点u为正在访问。对于u的每一个相邻顶点v，如果v未被访问，对v重复（3）操作，直至找到所有相邻顶点为止。置顶点u为已访问。

　　　　（4）若所有的顶点都被考察，则搜索停止。

ABCE BCE DCE
ADCE BDCE DE
AE BDE
ABDCE
ADE CE
ABDE

• 5.十字链表

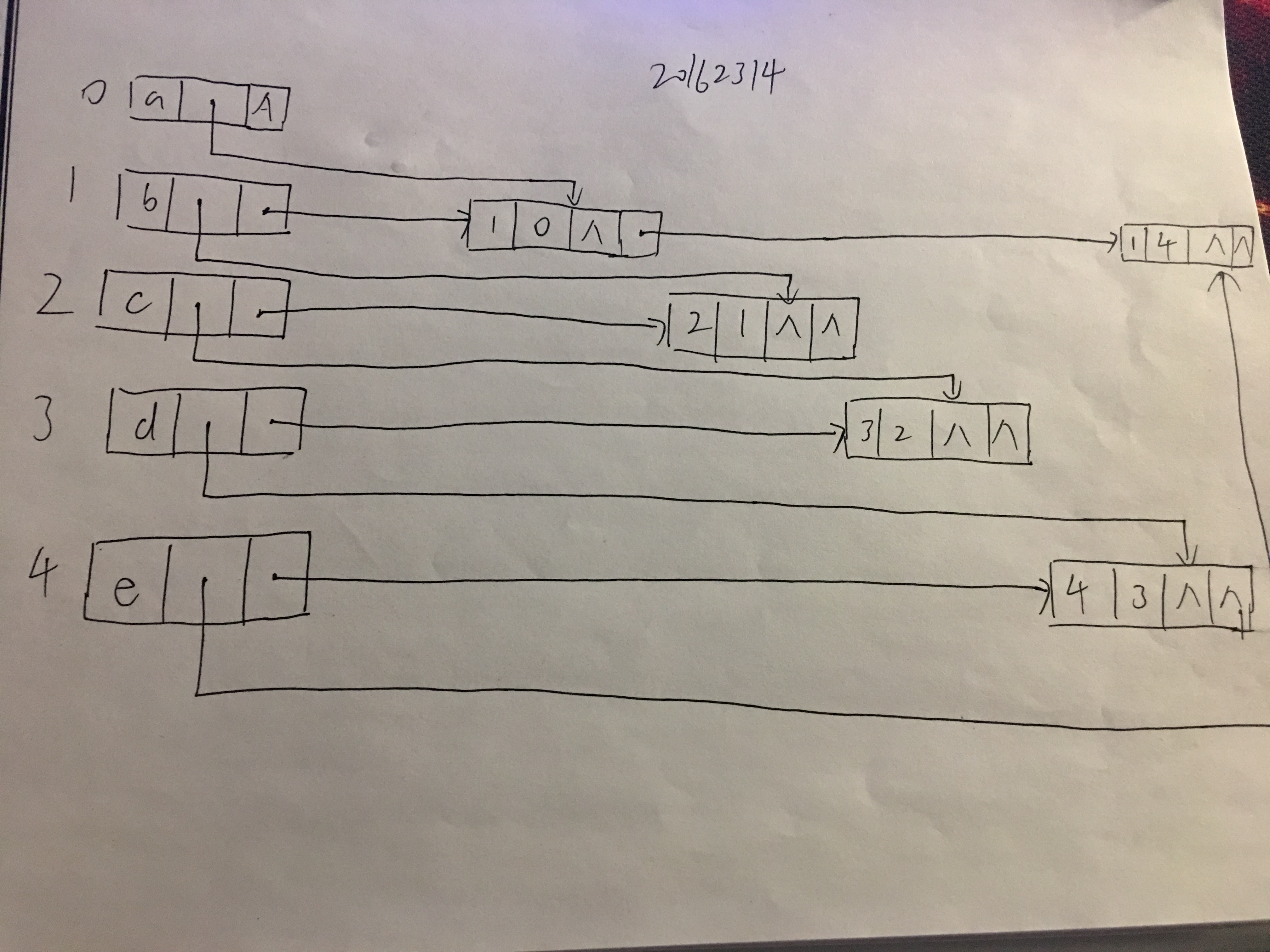
有向图的十字链表

十字链表（Orthogonal List)是有向图的另一种链式存储结构。可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中，对应于有向图中每一条弧都有一个结点，对应于每个定顶点也有一个结点。

• 6.构造哈夫曼树

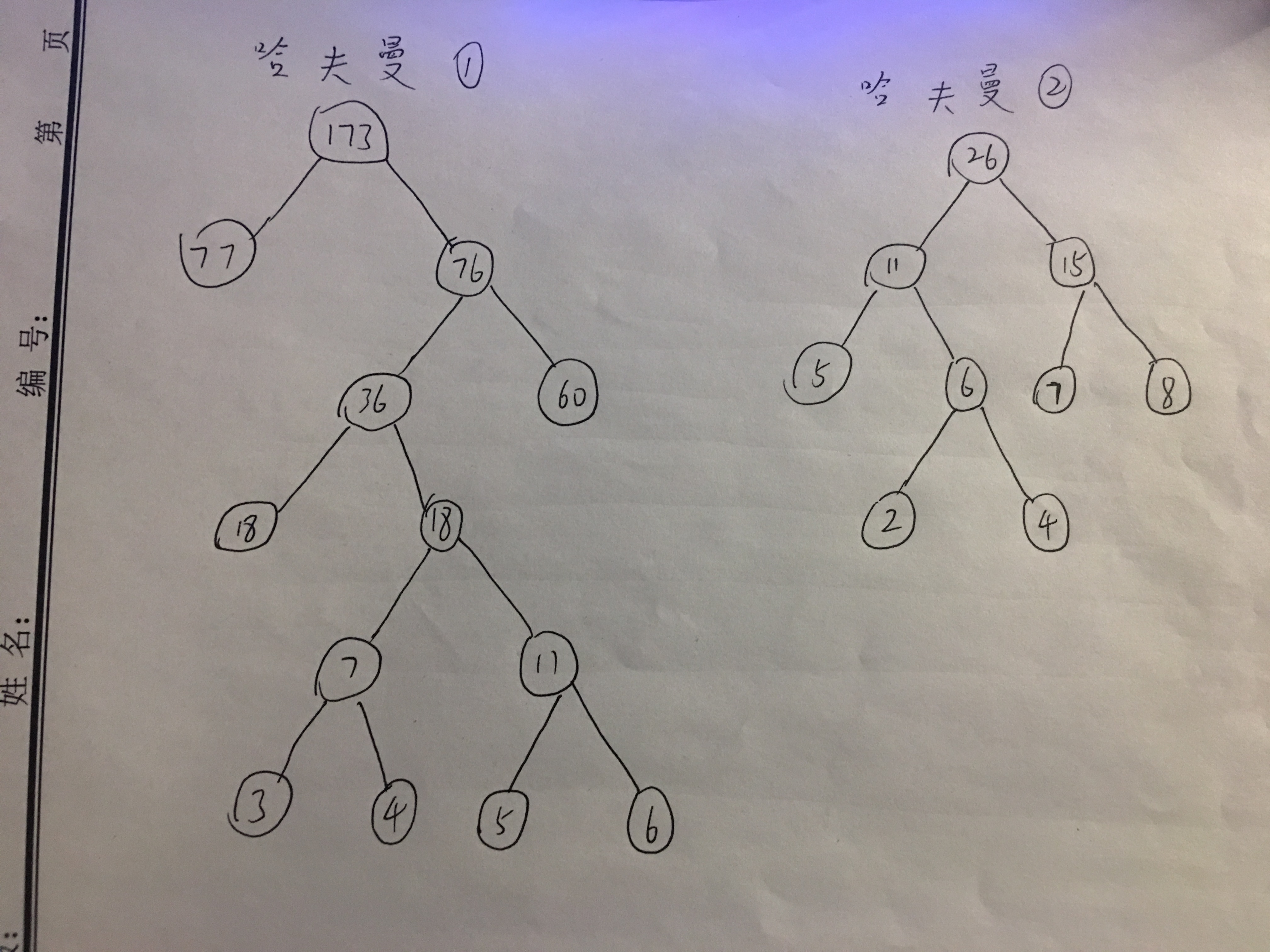
在作业本上分别针对权值集合W=（6，5，3，4，60，18，77）和W=（7，2，4，5，8）构造哈夫曼树

哈夫曼树的构造：假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，哈夫曼树的构造规则为：

1. 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；
2. 在森林中选出根结点的权值最小的两棵树进行合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
3. 从森林中删除选取的两棵树，并将新树加入森林；
4. 重复(02)、(03)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

• 7.中后序构建树

已知中，后序构建树

1、得到有后序序列的最后一个节点，设为a，除去最后一个节点前边序列为 S0

2、在中序序列中查找a的位置，其左边序列为S1,右部序列为S2,即 S1 a S2

3、根据S1、S2的长度将S0划分为两个序列S01, S02

4、该序列对应的根节点为a，左子树为根据后序序列S01和中序序列S0得到的子树，右子树为根据后序序列S11和中序序列S1得到的子树

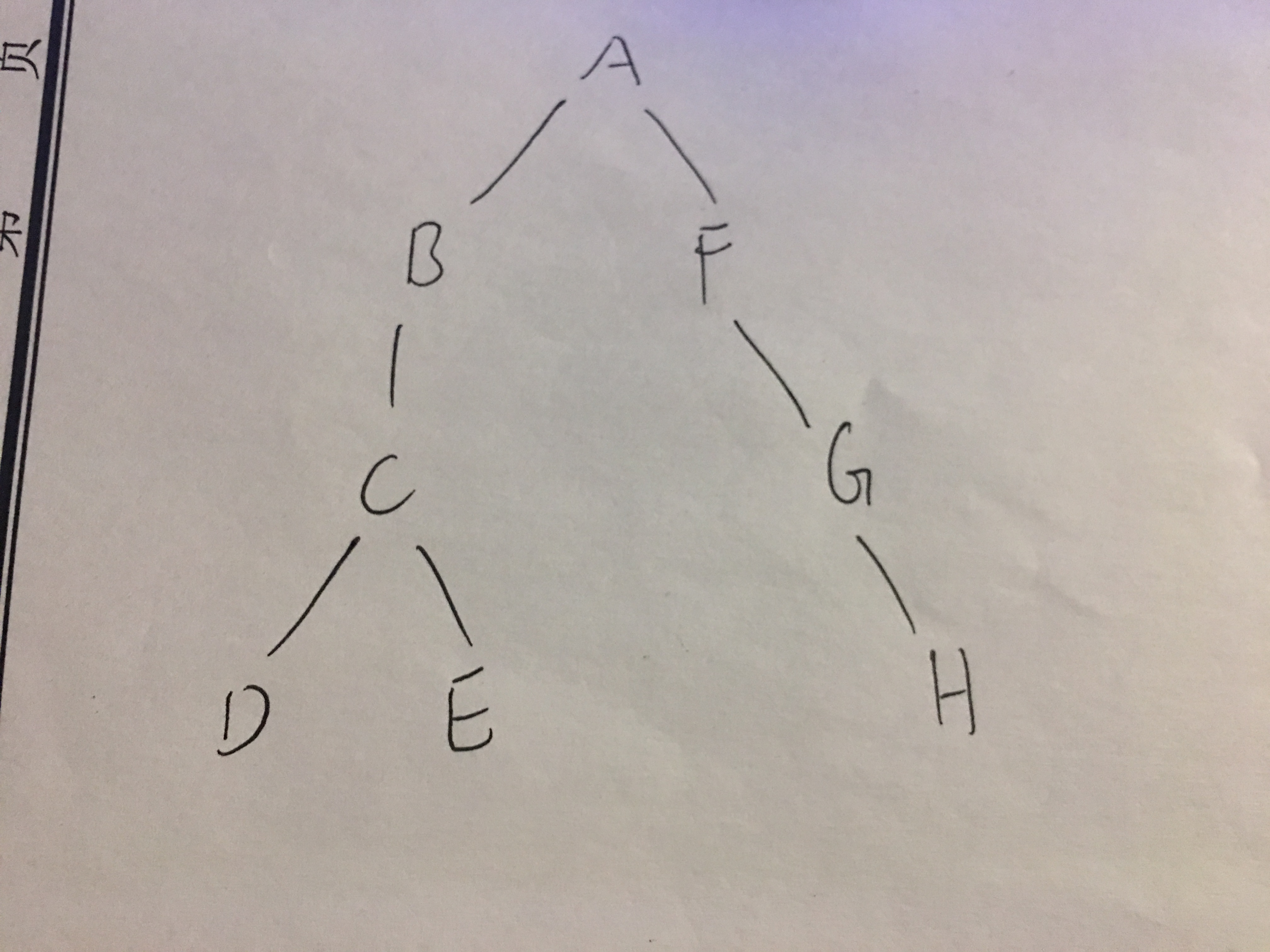
• 8.遍历树

中序
中序遍历（LDR）是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，先左后根再右。巧记：左根右。

D→B→H→E→K→I→A→F→C→G→J

• 9.树计算
  

树计算方法和技巧：
(1)在二叉树的第k 层上，最多有2k-1(k≥1)个结点，
(2)深度为m的二叉树最多有2m-1 个结点，
(3)度为0 的结点(即叶子结点)总是比度为2 的结点多一个，
(4)具有n 个结点的二叉树，其深度至少为[log2n]+1,其中[log2n] 表示取log2n 的整数部分，
(5)具有n 个结点的完全二叉树的深度为[log2n]+1

1、高度为7，叶节点数为50
2、至少2^{(h-1)个，至多2}h-1个
3、n2+2n3+3n4+...+(m-1)*nm+1

• 10.排序课堂测试

1 用JDB或IDEA单步跟踪对3 8 12 34 54 84 91 110进行快速排序的过程
2 提交第一趟完成时数据情况的截图，要全屏，包含自己的学号信息
3 课下把代码推送到代码托管平台

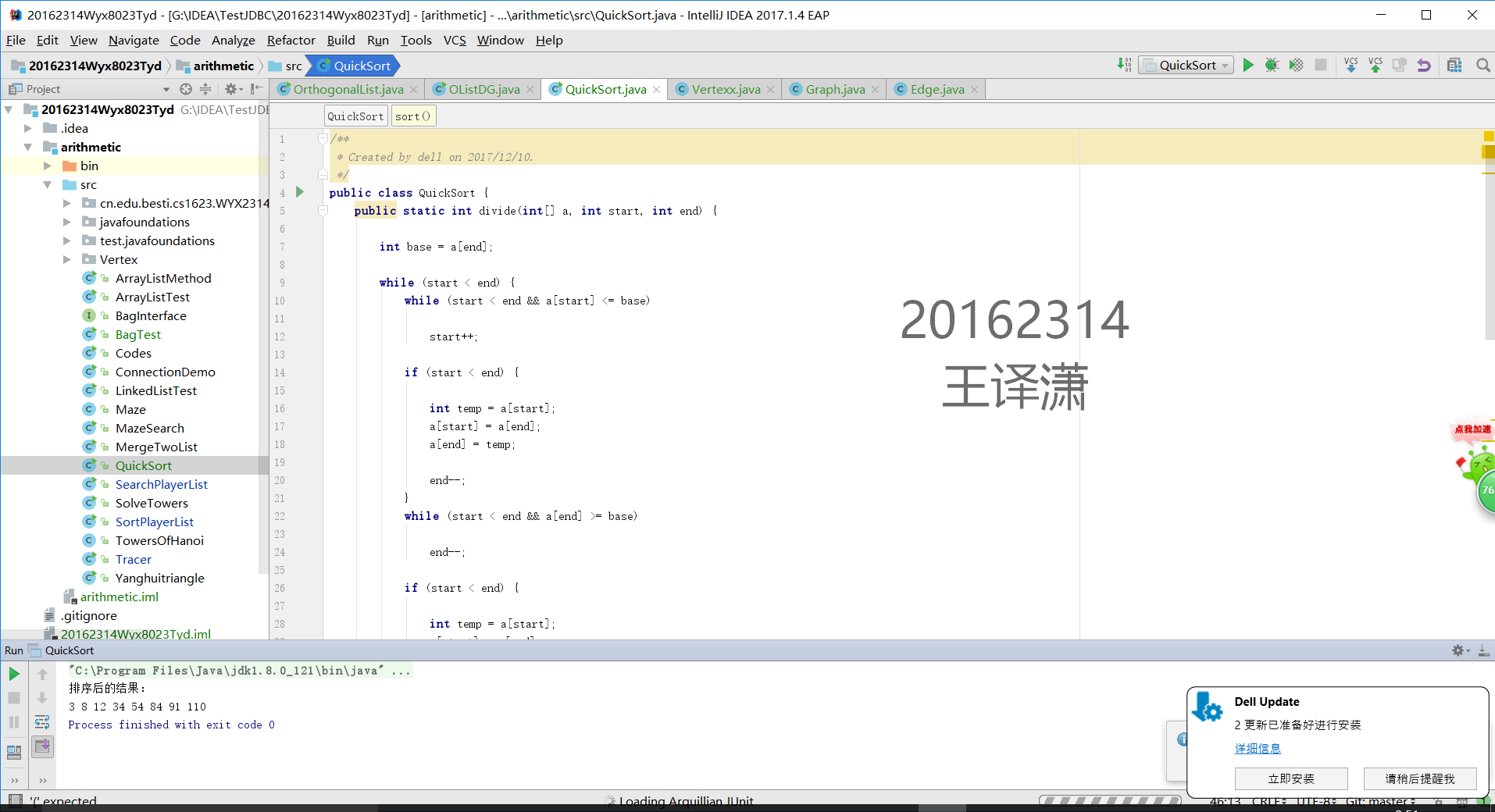
代码我压缩后微信上发给你。

• 11.查找课堂测试

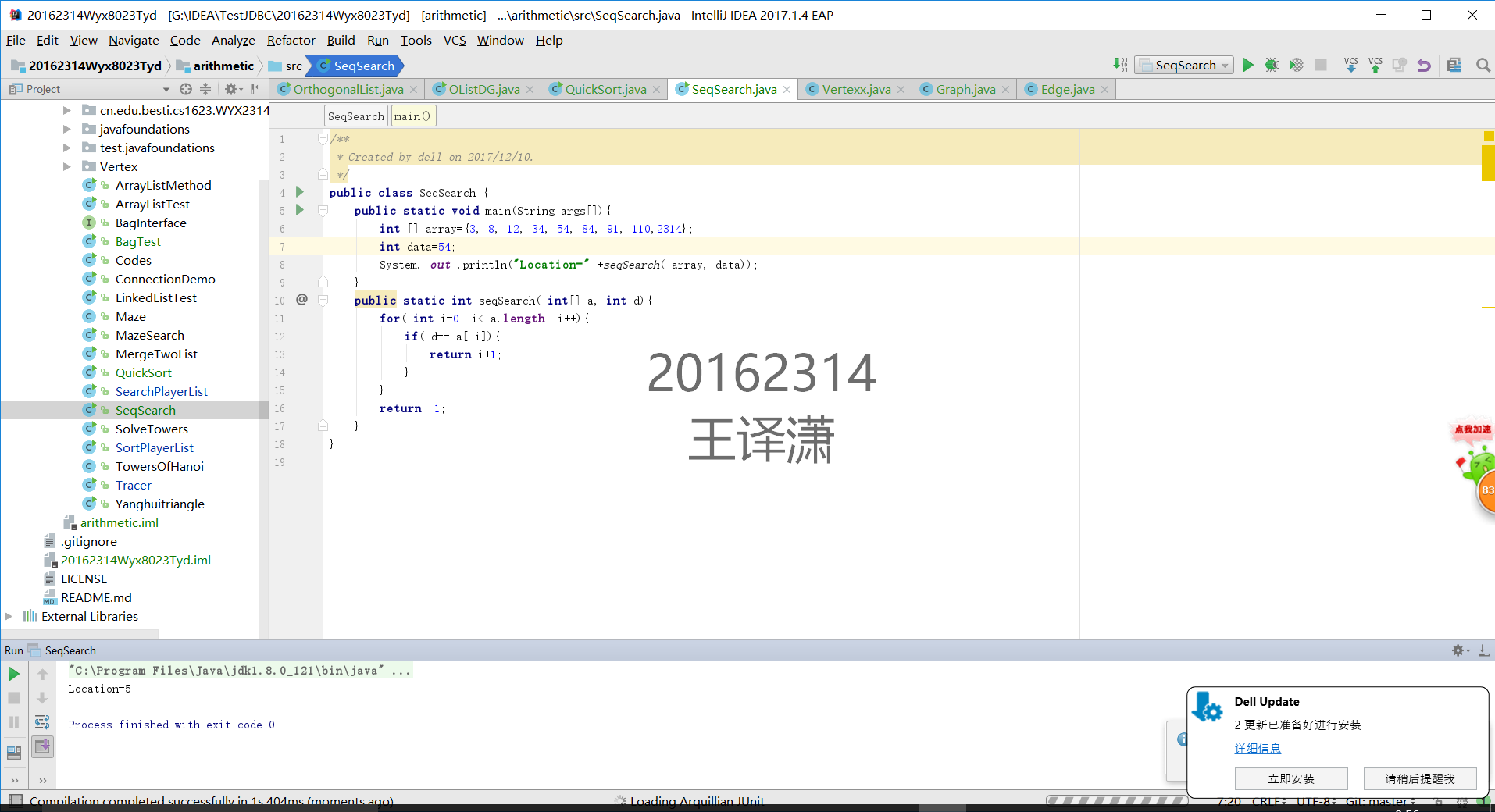
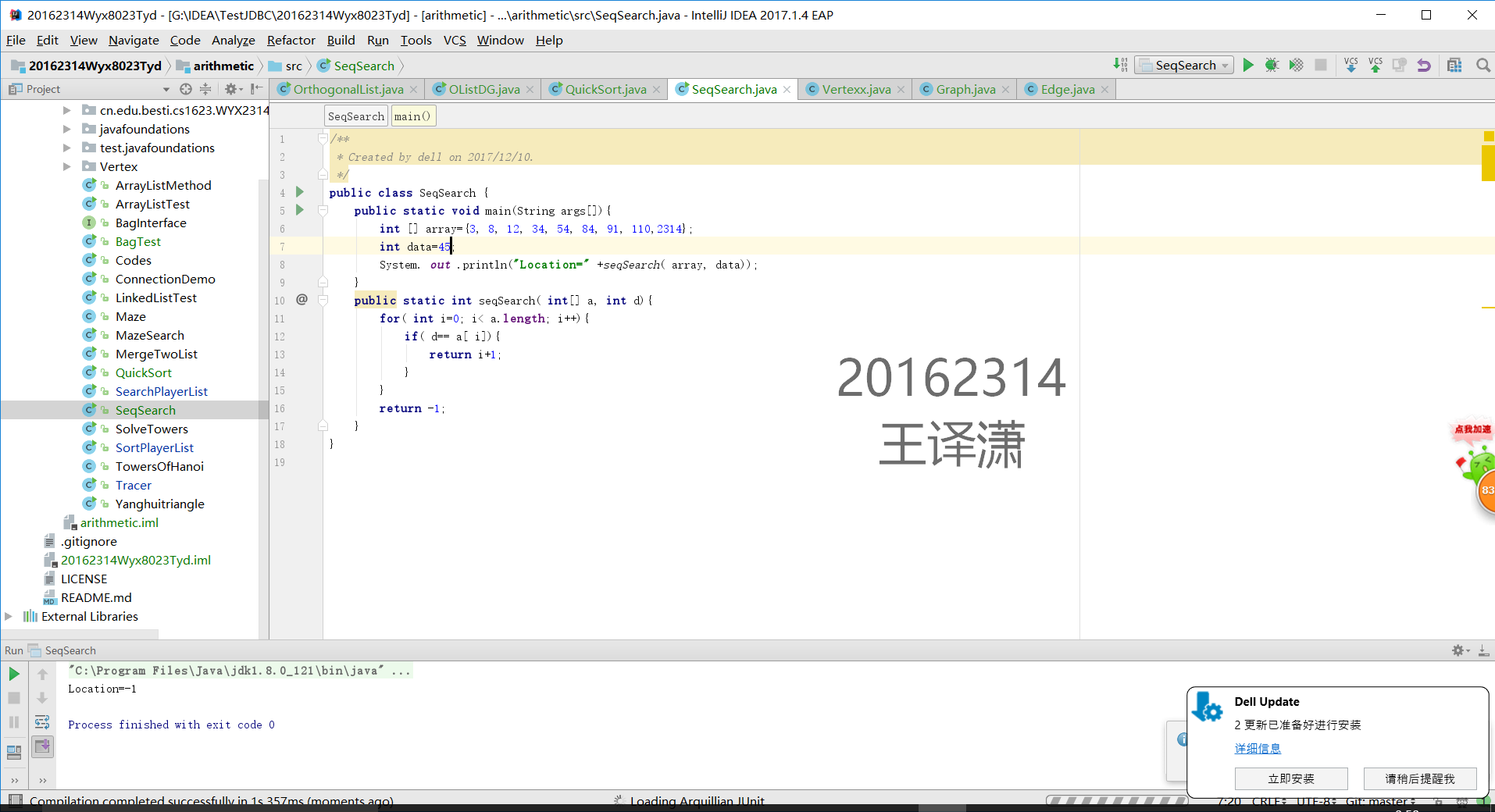
1 用JDB或IDEA单步跟踪在下列数据中（3 8 12 34 54 84 91 110）查找45和54的过程，对比使用顺序查找和二分查找的执行过程
2提交测试找到或找不到那一步的截图，要全屏，包含自己的学号信息
3课下把代码推送到代码托管平台

顺序查找54 （找到的那个）

顺序查找45（找不到的那个）

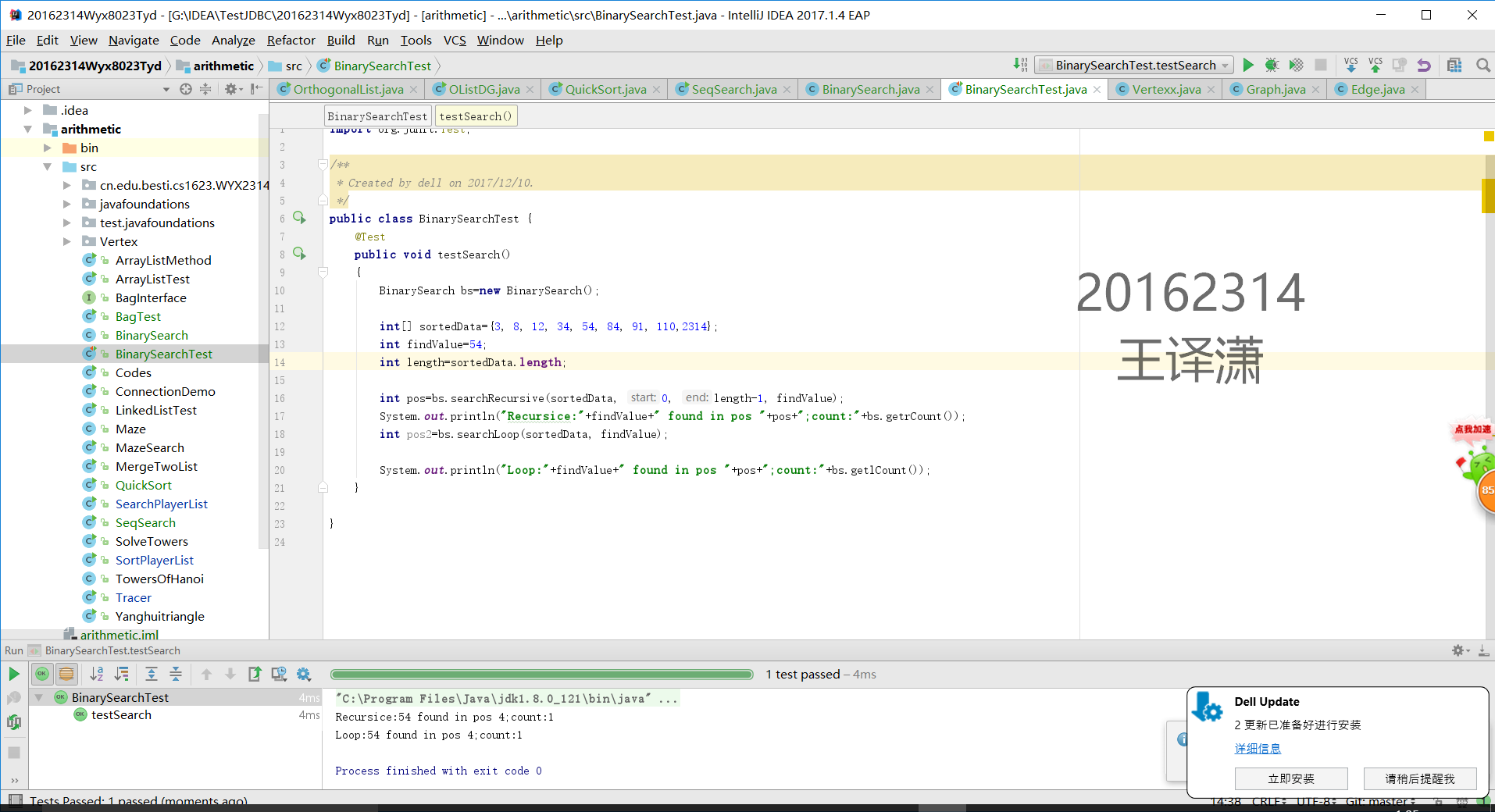
二分查找54（找到的那个）

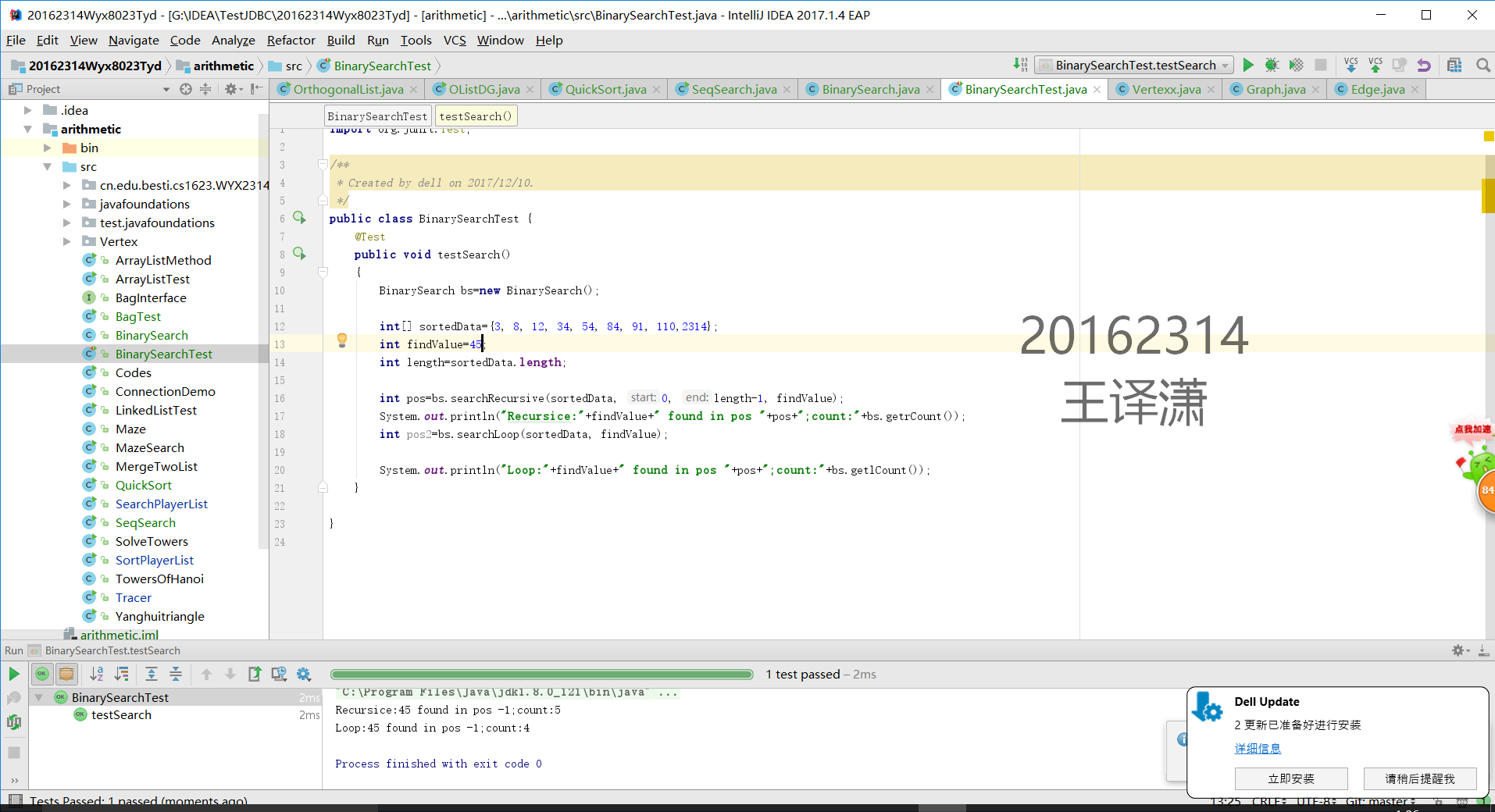
二分查找45（找不到的那个）

代码我微信上发给你