HDU 2084:https://vjudge.net/problem/HDU-2084
Problem Describe :
When it comes to the DP algorithm, a classic example is the tower problem, which is described as:There are towers as shown below, which require walking from the top to the bottom. If each step can only go to an adjacent node, what is the maximum number of nodes passing through?
Keyworld in problem is "maximun",so we can consider DP. After we think the problem,we can divide this problem into many subproblem,,The problem has the best substructure properties.If the solution to the subproblem contained in the optimal solution of the problem is also optimal, we call the problem the optimal substructure property.
Firstly,we can analyze the question and write the table which reflects the optimum solution of every elements.we use i and j to represent rows and columns.it has N rows and N columns,so we can draw N*N table.in this question ,5*5 is ok.
when i = N,then the optimum solution is element itself.
| 4 | 5 | 2 | 6 | 5 |
i = N-1,the optimum solution is max(i,j) = MAX{max(i+1,j),max(i+1,j+1)}+elem[i][j].
| 7 | 12 | 10 | 10 |
i = N-2 .. ... 1,follow above.
so the complete table is:
| 30 | ||||
| 23 | 21 | |||
| 20 | 13 | 10 | ||
| 7 | 12 | 10 | 10 | |
| 4 | 5 | 2 | 6 | 5 |
So the sate equation is:
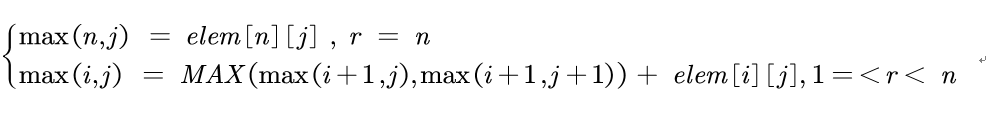
AC Code :
1 #include <iostream> 2 #include <algorithm> 3 #include <bits/stdc++.h> 4 using namespace std; 5 const int N = 101; 6 int Elem[N][N]; 7 int DP[N][N]; 8 int main() 9 { 10 int n,T; 11 cin>>T; 12 while(T--) 13 { 14 cin>>n; 15 for(int i = 1;i <= n;++i) 16 for(int j = 1;j <= i;j++) 17 cin>>Elem[i][j]; 18 for(int i = 1;i <= n;i++) 19 DP[n][i] = Elem[n][i]; 20 for(int i = n-1;i >= 1;--i) 21 for(int j = 1;j <= i;++j) 22 DP[i][j] = max(DP[i+1][j],DP[i+1][j+1])+Elem[i][j]; 23 cout<<DP[1][1]<<endl; 24 } 25 return 0; 26 }