【CF506E】Mr. Kitayuta's Gift
题意:给你一个字符串s,你需要在s中插入n个字符(小写字母),每个字符可以被插在任意位置。问可以得到多少种本质不同的字符串,使得这个串是回文的。答案对10007取模。
$|s|le 200,nle 10^9$
题解:神题。
首先由于题目要求本质不同,所以我们为了防止重复,考虑从两边向中间不断复原回文串,如果新加入的字符与s两端(或一端)的字符相同,则匹配成功,继续匹配下一个字符。也就是说我们取的是s在回文串中最外面的出现位置。
为了方便,我们先只考虑n+|s|为偶数的情况,可以设出DP状态:设f[i][a][b]表示从外往里加入了i个字符,原串左边匹配到了a,有边匹配到了b的方案数。当新加入一个字符时,我们根据它是否与a和b匹配来确定转移到哪个状态。我们发现这个过程其实是在一个有限状态自动机上匹配的过程。对于s=abaac,转移的过程如下图:
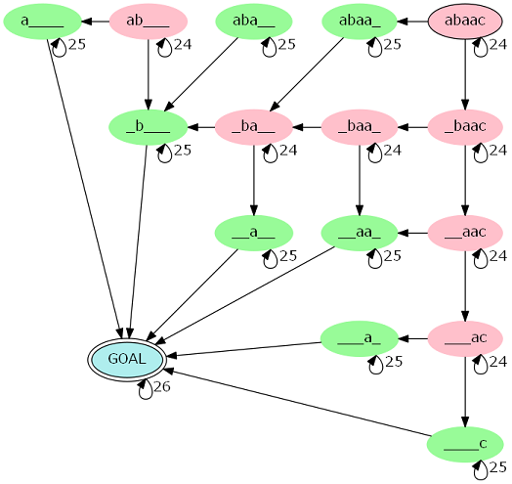
其中GOAL代表匹配完毕,它之后可以接任何字符,所以有26条自环。对于红点,它代表的状态两端的字符不相同,所以他有2条出边,24条自环。对于绿点,它代表的状态两端的字符相同,所以有1条出边和25条自环。特别地,能转移到GOAL的点都是绿点。
直接建出来这个自动机显然节点数目是$|s|^2$的,无法用矩乘优化。所以我们考虑对这个自动机进行压缩。可以发现,整个自动机其实可以被拆成若干条链,其中一条链上如果有i个红点,就有$lceil {|s|-iover 2} ceil$个绿点。既然我们已经把自动机拆成链了,那么每条链上红点绿点的顺序也就无关紧要了,我们只需要知道每条链上红点与绿点的数目。换句话说,我们需要知道有多少条链有i个红点,这样一来本质不同的链就只有|s|条了。
统计方法比较简单,用g[a][b][i]表示在所有从起始节点走到(i,j)这个节点的路径中,有多少条已经走了i个红点。转移复杂度$|s|^3$。
既然我们已经有了|s|种链的各自数目,我们就可以想办法用$O(|s|)$个节点来构建一个新的自动机了。到这里我的方法和官方做法出现了分歧,个人认为我的做法比较简单。
构建|s|个红点串成一串,从起点指出来;$lceil{|s|over 2} ceil$个绿点串成一串,指向终点。对于一种串$(i,lceil {|s|-iover 2} ceil)$,我们从第i个红点向第$lceil {|s|-iover 2} ceil$个绿点连一条边即可。这样一来点数就是${3over 2}|s|$,可以用矩乘优化。如下图:
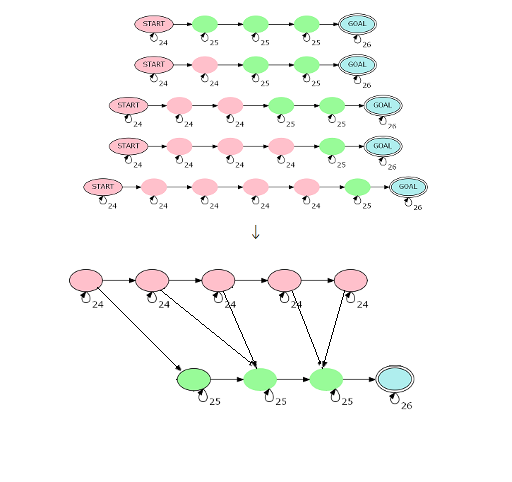
那么对于n+|s|为奇数的情况呢?我们先进行$n+|s|+1over 2$步矩乘,但是在最后一步时形如(i,i+1)的绿点是不能直接转移到终点的。于是我们要将这些转移的贡献减去,方法是将(i,i+1)这样的点设为终点(无自环),重新建图跑一边矩乘即可。
本题的矩乘优化常数小技巧:发现我们只能从编号小的点转移到编号大的点,所以j只需要从i枚举到n,k只需要从i枚举到j即可。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int P=10007;
int n,m,N;
int f[210][210][210],g[210];
struct M
{
int v[310][310];
int * operator [] (const int &a) {return v[a];}
M () {memset(v,0,sizeof(v));}
inline M operator * (const M &a) const
{
M b;
int i,j,k;
for(i=0;i<=N;i++) for(j=i;j<=N;j++) for(k=i;k<=j;k++) b.v[i][j]=(b.v[i][j]+v[i][k]*a.v[k][j])%P;
return b;
}
}S,T;
char str[210];
inline void pm(int y)
{
while(y)
{
if(y&1) S=S*T;
T=T*T,y>>=1;
}
}
int main()
{
scanf("%s%d",str,&m),n=strlen(str);
int i,j,k;
f[0][n-1][0]=1;
for(i=0;i<n;i++)
{
for(j=n-1;j>=i;j--)
{
if(str[i]==str[j])
{
for(k=0;k<i+n-j;k++)
{
if(i+1<j) f[i+1][j-1][k]=(f[i+1][j-1][k]+f[i][j][k])%P;
else g[k]=(g[k]+f[i][j][k])%P;
}
}
else
{
for(k=0;k<i+n-j;k++)
{
f[i+1][j][k+1]=(f[i+1][j][k+1]+f[i][j][k])%P;
f[i][j-1][k+1]=(f[i][j-1][k+1]+f[i][j][k])%P;
}
}
}
}
N=n+(n+1)/2+1;
S[0][1]=1,S[0][N-(n+1)/2]=g[0],T[N][N]=26;
for(i=1;i<=n;i++)
{
T[i][i]=24,T[i][N-(n-i+1)/2]=g[i];
if(i!=n) T[i][i+1]=1;
}
for(i=n+1;i<N;i++) T[i][i+1]=1,T[i][i]=25;
if((n+m)&1)
{
pm((n+m+1)>>1);
int ans=S[0][N];
memset(S.v,0,sizeof(S.v));
memset(T.v,0,sizeof(T.v));
memset(g,0,sizeof(g));
for(i=0;i<n-1;i++) if(str[i]==str[i+1]) for(k=0;k<=n;k++)
{
g[k]=(g[k]+f[i][i+1][k])%P;
}
S[0][1]=1,S[0][N-(n+1)/2]=g[0];
for(i=1;i<=n;i++)
{
T[i][i]=24,T[i][N-(n-i+1)/2]=g[i];
if(i!=n) T[i][i+1]=1;
}
for(i=n+1;i<N;i++) T[i][i+1]=1,T[i][i]=25;
pm((n+m+1)>>1);
printf("%d",(ans-S[0][N]+P)%P);
}
else
{
pm((n+m)>>1);
printf("%d",S[0][N]);
}
return 0;
}//abaac 2