【题目】
【描述】
给n个整数a[1],...,a[n],满足0<=a[i]<=2^k-1。Vanya可以对这n个数中任一多个数进行操作,即将x变为x',其中x'指x限制在k位内二进制取反。问a[1],...,a[n]中最多有多少个连续子段的异或和不为0。
数据范围:1<=n<=200000,1<=k<=30
【思路】
为了叙述方便,记MAX=(1<<k)-1,即二进制下k位全是1的数。
为了符号表示不产生歧义,以下使用^表示异或(上面的题目描述中指的是次方)。
这里要用到异或运算的一个很重要的性质,即x^x=0。
根据定义,x^x'=MAX,从而x'=x^x^x'=x^MAX。
先不考虑a[1],...,a[n]的变化。维护前缀异或和s[i],于是a[i]^...^a[j]=s[j]^s[i-1]。那么,a[i]^...^a[j]==0当且仅当s[j]==s[i-1]。为了让连续子段异或和为0尽量少,就是要让s[i]尽量不同。
再看改变某个a[i]会带来的影响。将某个a[i]变为a[i]^MAX,那么包含a[i]的前缀异或和s[j]都要变为s[j]^MAX,即s[j]变为s[j]^MAX对所有j>=i。这个时候发现,如果再改变a[i+1],则s[k]又都变回去了对所有k>=i+1。这说明可以通过改变某些a[i]实现将某一个s[j]变为s[j]^MAX。
这个时候有个很自然的想法就是,值为x和x^MAX的那些s[i]应该放在一类中考虑,因为它们最多只有两个值,要想使得“在其中挑两个数,它们不相等”的概率最小,只能让取x和x^MAX的数字个数尽量平均,即相等或者相差1。
确定s[i]的取值之后(有多少个s[i]取某个值x或者x^MAX),记第k个取值的s[i]共有nk个,于是最终的答案为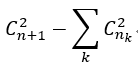 。
。
注意:要注意取值范围,要开long long!【比赛中第一次提交就因为这个问题WA了……
【我的实现】

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cmath> 5 #include <algorithm> 6 7 using namespace std; 8 #define MaxN 200030 9 10 long long s[MaxN]; 11 12 int main() 13 { 14 long long n, k; 15 long long i, j; 16 long long cnt, ans, tmp; 17 long long x; 18 long long MAX; 19 //scanf("%d%d", &n, &k); 20 cin >> n >> k; 21 MAX = (1<<(long long)k)-1; 22 s[0] = 0; 23 for(i = 1; i <= n; i++) 24 { 25 cin >> x; 26 s[i] = s[i-1] ^ x; 27 } 28 for(i = 0; i <= n; i++) 29 s[i] = min(s[i], MAX^s[i]); 30 sort(s, s+n+1); 31 cnt = 0; 32 ans = (n+1) * n / 2; 33 for(i = 0; i <= n; i++) 34 { 35 if(i == 0 || s[i] == s[i-1]) 36 cnt++; 37 else 38 { 39 if(cnt % 2) //奇数 40 { 41 tmp = cnt / 2; 42 ans -= tmp * (tmp-1) / 2; 43 tmp = cnt / 2 + 1; 44 ans -= tmp * (tmp-1) / 2; 45 } 46 else 47 { 48 tmp = cnt / 2; 49 ans -= tmp * (tmp-1); 50 } 51 cnt = 1; 52 } 53 } 54 if(cnt % 2) //奇数 55 { 56 tmp = cnt / 2; 57 ans -= tmp * (tmp-1) / 2; 58 tmp = cnt / 2 + 1; 59 ans -= tmp * (tmp-1) / 2; 60 } 61 else 62 { 63 tmp = cnt / 2; 64 ans -= tmp * (tmp-1); 65 } 66 cout<< ans; 67 return 0; 68 }
【评测结果】

