一、问题描述
在电子电路设计中,我们常常需要将多个组件连接在一起,显然我们希望所用的线能够最短,由此引出最小生成树问题。
在本实验中,我们将讨论解决最小生成树问题的两种算法:Prim算法和Kruskal算法。其中Prim算法的时间复杂度为O(N^2),如果使用二叉堆来优化寻找新加入的结点,则可以将时间复杂度降到O(E logN),如果使用斐波那契堆,时间复杂度将改善为O(E+N logN);Kruskal算法的时间复杂度为O(E logE)。
本实验根据算法的不同,对图的存储方式也是不一样的。在Prim算法中,使用邻接表存储图;而在Kruskal算法的实现中,考虑到实现的方便,直接存储了边的相关信息。具体实现下面将会给出。
二、数据结构——邻接表
1、邻接表(Prim算法)
邻接表是图的一种链式存储结构。首先有一个包含所有结点的顺序表,顺序表的每个元素对应一个单链表,表示从该结点出发的弧。每个结点由3部分组成:指针域,指向从当前结点出发的下一条弧的尾结点;尾结点标号;数据域,保存当前弧的信息,比如权重等等。
需要说明的是,这适用于有向图与无向图,不妨认为无向图的边u--v就是有向图的两条弧u->v与v->u。
2、另一种存储图的方式(Kruskal算法)
由Kruskal算法的特点,为了方便找边,我们可以直接用一个“集合”(可以用静态查找表实现,这里的集合的意思是边之间没有逻辑关系)保存所有的边。“集合”中的每个结点由3部分组成:结点1、结点2和当前边的信息(比如权重)。
可以看出,这样的方式更适合于存储无向图,且对点的信息的访问需求不大,否则将会增大查询的时间复杂度。
三、算法的设计和实现
1、Prim算法
(1)简述
Prim算法的工作原理与解决单源点最短路的Dijkstra算法相似。我们定义一个集合A,在集合A里面的所有结点已经形成了一棵最小生成树;然后不断向其添加新结点,使得集合A的性质保持不变,直到网络中的所有结点加入到集合A中,算法终止;此时,得到一棵最小生成树。
本策略属于贪心策略,保证每次添加的结点所对应的新边是权重增加得最小的。
(2)伪代码
1 Prim(G, w, x) 2 for each u∈G.V 3 u: cost = ∞ 4 u: father = NULL 5 x: cost = 0 6 for k: 2 to n 7 u = MinCost(A) //表示从A出发到VA的最短弧的尾结点 8 for each v∈G.adj[u] 9 if v∈G && w(u, v) < v: cost 10 v: father = u 11 v: cost = w(u, v) 12 Add v into A
(3)时间复杂度分析
由伪代码可以看出,Prim算法的时间复杂度为O(n^2)。
为了减小算法的时间复杂度,需要找一种更高效的选择新边的方法。由于是寻找最小的边,可以维护一个优先队列,队列排序的关键字为cost,即集合A中的结点到达某个点的最小花费。我们约定,如果不存在这样的边,则v: cost = ∞;集合A中的结点有v: cost = 0。此时,算法的运行时间取决于优先队列的实现方式。
如果用二叉堆来实现,算法的总时间代价为O(E logN);如果使用斐波拉契堆来实现,算法的运行时间将改进到O(E + N logN)。
2、Kruskal算法
(1)简述
Kruskal算法也属于贪心算法。每次选择一条连接两个不同的连通分量的最短的边,加入到森林,直到添加了n-1条边,得到一棵树,就是需要找的最小生成树。
(2)伪代码
1 Kruskal(G, w) 2 A = ∅ 3 for each v∈G.V 4 Make_Set(v) 5 将G.E的边不递减排序 6 for each edge(u, v)∈G.E //按照不递减顺序访问,直到加入n-1条边 7 if Find_Set(u) != Find_Set(v) //两结点不在同一连通分量 8 Add (u, v) into A 9 Union(u, v) //合并两个连通分量
(3)时间复杂度分析
排序可以使用快排,时间复杂度为O(E logE)。合并两个连通分量时,可以使用并查集且使用路径压缩的方式优化,总运行时间为O((N + E)α(N))。所以Kruskal算法的时间复杂度为O(E logE)。
3、MST性质及其证明
(1)MST性质:设G=(N,E)是一个在边E上定义了实数值权重函数w的连通无向图。设集合A为E的一个子集,且A包括在图G的某棵最小生成树中,设(S,N-S)是图G中尊重集合A的任意一个切割(如果一条边(u,v)∈E的一个端点位于集合S,另一个断点位于集合N-S,则称该条边横跨切割(S,N-S)。如果集合A中不存在横跨该切割的边,则称该切割尊重集合A),又设(u,v)是横跨切割(S,N-S)的一条轻量级边。那么边(u,v)对于集合A是安全的(对于(u,v),如果加入集合A后,使得A不违反循环不变式,即A∪{(u,v)}也是某棵最小生成树的子集,则称(u,v)为集合A的安全边)。
(2)证明:(证明参考《算法导论》)
设T是一棵包括A的最小生成树,假设T不包含轻量级边(u,v)。
边(u,v)与T中从结点u到结点v的简单路径p形成一个环路,如下图。由于结点u和结点v分别处在切割(S,N-S)的两端,T中至少有一条边属于简单路径p并且横跨该切割。设(x,y)为这样的一条边。因为切割(S,N-S)尊重集合A,故边(x,y)不在集合A中。由于边(x,y)位于T中从u到v的唯一简单路径上,将该条边删除会导致T被分解为两个连通分量。将(u,v)加上去可以将这两个连通分量连接起来,形成一棵新的生成树T’=T{(x,y)}∪{(u,v)}。
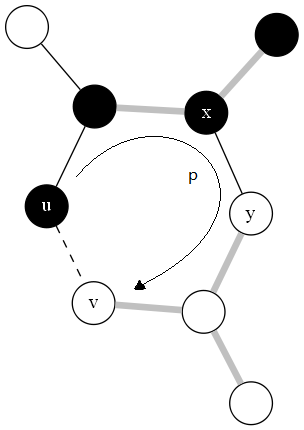
如图,黑色结点位于集合S里,白色结点位于集合N-S里。图中仅描述了最小生成树T中的边,而没有绘出图G中的其他边。集合A中的边都为灰色粗边,边(u,v)是横跨(S,N-S)的一条轻量级边。边(x,y)是树T里面从结点u到结点v的唯一简单路径上的一条边。要形成一棵包含(u,v)的最小生成树T’,只需要在T中删除边(x,y),然后加上边(u,v)即可。
下证T’为一棵最小生成树。
由于边(u,v)是横跨切割(S,N-S)的一条轻量级边,且(x,y)也横跨该切割,所以w(u,v)<=w(x,y)。因此,w(T’) = w(T) - w(x,y) + w(u,v) <= w(T)。又T是一棵最小生成树,从而有w(T) = w(T’),故T’也是一棵最小生成树。
下证边(u,v)对于集合A是安全的。
由于A包含于T,且(x,y)∉A,所以A包含于T’;因此A∪{(u,v)}包含于T’。由于T’是最小生成树,故边(u,v)对于集合A是安全的。证毕。
四、预期结果和实验中的问题
1、预期结果
程序可以正确地找出图中的一棵最小生成树。
当最小生成树唯一存在时,所找到的最小生成树是唯一的;当最小生成树存在不唯一时,算法将会找出其中一棵生成树,当然程序每次运行所找出的最小生成树都是相同的。
2、实验中的问题及思考
(1)次小生成树
a)定义:设G=(N,E)为一连通无向图,其权重函数为w,假定|E| >= |N|并且所有的权重都互不相同。设τ为G的所有生成树的集合,T’为G的一棵最小生成树,T是一棵生成树,若满足w(T) = min{w(T’’)},T’’∈τT’,则称T是一棵次小生成树。
b)还没想出除了暴力搜索以外的算法。
(2)瓶颈生成树
a)定义:无向图G的瓶颈生成树T是G的一棵生成树,其最大边的权重是G的所有生成树中最小的。
b)可以发现,最小生成树都是瓶颈生成树,而瓶颈生成树不一定都是最小生成树。
附:c++源代码:
1、Prim算法实现

1 /* 2 项目:最小生成树——Prim算法 3 作者:张译尹 4 */ 5 #include <iostream> 6 #include <cstdio> 7 #include <cstring> 8 9 using namespace std; 10 #define MaxN 120 //结点数 11 12 //结点 13 struct node 14 { 15 int v, w; 16 node *next; 17 }; 18 19 //图 20 class My_graph 21 { 22 private: 23 //NodeList L; 24 node *adj[MaxN]; //单链表头指针 25 int len; //链表长度(结点个数) 26 27 int VexNum, ArcNum; //图的结点数和边数 28 int Kind; //图的种类:0-无向图,1-有向图 29 public: 30 void Init(int vNum, int kind) 31 { 32 VexNum = vNum; 33 ArcNum = 0; 34 Kind = kind; 35 36 //L.Init(); 37 memset(adj, 0, sizeof(adj)); 38 len = 0; 39 } 40 void D_Addedge(int u, int v, int w) //u->v,权值为w。有向图 41 { 42 node *p = new node; 43 p -> v = v; 44 p -> w = w; 45 p -> next = adj[u]; 46 adj[u]= p; 47 } 48 void UD_Addedge(int u, int v, int w) //u->v,权值为w。无向图 49 { 50 node *p = new node; 51 p -> v = v; 52 p -> w = w; 53 p -> next = adj[u]; 54 adj[u]= p; 55 56 p = new node; 57 p -> v = u; 58 p -> w = w; 59 p -> next = adj[v]; 60 adj[v]= p; 61 } 62 void Addedge(int u, int v, int w) 63 { 64 if(Kind == 0) 65 UD_Addedge(u, v, w); 66 else 67 D_Addedge(u, v, w); 68 ArcNum++; 69 } 70 int Get_VexNum() 71 { 72 return VexNum; 73 } 74 void Prim() 75 { 76 int i, j; 77 int n = VexNum, Ans = 0; 78 int cost[MaxN], MinCost; 79 int fa[MaxN], v, x; 80 bool vis[MaxN]; 81 memset(cost, 0x3f, sizeof(cost)); 82 memset(vis, false, sizeof(vis)); 83 84 cost[1] = 0; //选择了结点1 85 vis[1] = true; 86 fa[1] = 1; 87 for(node *p =adj[1]; p != NULL; p = p -> next) 88 { 89 cost[p -> v] = p -> w; 90 fa[p -> v] = 1; 91 } 92 93 for(i = 2; i <= n; i++) //寻找第i个结点 94 { 95 MinCost = 0x3f; 96 v = -1; 97 for(j = 1; j <= n; j++) 98 { 99 if(!vis[j] && cost[j] < MinCost) 100 { 101 v = j; 102 MinCost = cost[j]; 103 } 104 } 105 if(v != -1) 106 { 107 vis[v] = true; //将v加入 108 printf("(%d %d): %d ", fa[v], v, MinCost); 109 110 Ans += MinCost; 111 for(node *p = adj[v]; p != NULL; p = p -> next) 112 { 113 x = p -> v; 114 if(!vis[x] && cost[x] > (p -> w)) 115 { 116 cost[x] = p -> w; 117 fa[x] = v; 118 } 119 } 120 } 121 } 122 printf("最小生成树的权值和为:%d ", Ans); 123 } //Prim 124 }; 125 126 void Read_and_Build(My_graph &G) 127 { 128 int n, m, Kind; 129 int u, v, w; 130 int i; 131 //My_graph G; 132 133 printf("请输入图的类型:1为有向图,0为无向图。 "); 134 scanf("%d", &Kind); 135 136 printf("请输入图的结点数和边数,用空格隔开。 "); 137 scanf("%d%d", &n, &m); 138 G.Init(n, Kind); 139 140 printf("请输入图中所有的边,格式为空格相隔的3个数,有向图表示“起始点 结束点 边权”,无向图表示“点1 点2 边权”。其中结点的标号范围为[1,n]。 "); 141 for(i = 1; i <= m; i++) 142 { 143 scanf("%d%d%d", &u, &v, &w); 144 G.Addedge(u, v, w); 145 } 146 } 147 148 int main() 149 { 150 My_graph G; 151 Read_and_Build(G); 152 G.Prim(); 153 return 0; 154 }
2、Kruskal算法实现

1 /* 2 项目:最小生成树——Kruskal算法 3 作者:张译尹 4 */ 5 #include <iostream> 6 #include <cstdio> 7 #include <cstring> 8 #include <algorithm> 9 10 using namespace std; 11 #define MaxN 120 //结点数 12 #define MaxM 10020 //边数 13 14 //边 15 struct E 16 { 17 int u, v, w; 18 }; 19 20 class My_graph 21 { 22 private: 23 E Edge[MaxM]; //边 24 25 int VexNum, ArcNum; //图的结点数和边数 26 public: 27 void Init(int vNum) 28 { 29 VexNum = vNum; 30 ArcNum = 0; 31 memset(Edge, 0, sizeof(Edge)); 32 } 33 void Addedge(int u, int v, int w) //u->v,权值为w 34 { 35 ArcNum++; 36 Edge[ArcNum].u = u; 37 Edge[ArcNum].v = v; 38 Edge[ArcNum].w = w; 39 } 40 static bool Cmp(E a, E b) 41 { 42 return (a.w) < (b.w); 43 } 44 int Find(int x, int fa[]) 45 { 46 if(fa[x]==-1) 47 return x; 48 return fa[x]=Find(fa[x], fa); 49 } 50 void Kruskal() 51 { 52 sort(Edge + 1, Edge + ArcNum + 1, Cmp); 53 int i, j = 1; 54 int u, v; 55 int fa[MaxN]; 56 int Ans = 0; 57 memset(fa, -1, sizeof(fa)); 58 for(i = 1; i <= VexNum - 1; i++) 59 { 60 while(j <= ArcNum) 61 { 62 u = Edge[j].u; u = Find(u, fa); 63 v = Edge[j].v; v = Find(v, fa); 64 if(u != v) 65 { 66 if(u > v) 67 swap(u, v); 68 fa[v] = u; 69 Ans += Edge[j].w; 70 printf("(%d,%d):%d ", u, v, Edge[j].w); 71 j++; 72 break; 73 } 74 j++; 75 } 76 } 77 printf("最小生成树的权值和为:%d ", Ans); 78 } //Kruskal 79 }; 80 81 void Read_and_Build(My_graph &G) 82 { 83 int n, m; 84 int u, v, w; 85 int i; 86 //My_graph G; 87 88 printf("请输入图的结点数和边数,用空格隔开。 "); 89 scanf("%d%d", &n, &m); 90 G.Init(n); 91 92 printf("请输入图中所有的边,格式为空格相隔的3个数,表示“点1 点2 边权”。其中结点的标号范围为[1,n]。 "); 93 for(i = 1; i <= m; i++) 94 { 95 scanf("%d%d%d", &u, &v, &w); 96 G.Addedge(u, v, w); 97 } 98 } 99 100 int main() 101 { 102 My_graph G; 103 Read_and_Build(G); 104 G.Kruskal(); 105 return 0; 106 }
