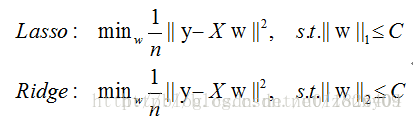概述
针对某种数据,通过一定的特征提取手段,或者记录观测到的特征,往往得到的是一组特征,但其中可能存在很多特征与当前要解决的问题并不密切等问题。另一方面,由于特征过多,在处理中会带来计算量大、泛化能力差等问题,即所谓的“维数灾难”。
特征选择便是从给定的特征集合中选出相关特征子集的过程。特征选择也可以有效地解决维数灾难的难题。具体而言:降维从一定程度起到了提炼优质低维属性和降噪的效果,特征选择则是直接剔除那些与学习任务无关的属性而选择出最佳特征子集。因此为特征维度进行约减是有必要的,我们希望在保证分类等任务效果的同时,使用尽可能少的特征完成分类。
以下从两个环节:子集搜索、特征/特征子集评价,三种分类:过滤式、包裹式和嵌入式,进行展开。
特征子集搜索
1、单独衡量特征

2、考虑已选择特征的方法


3、顺序后向选择

4、顺序前向选择

5、增l减r选择法


6、浮动搜索技术




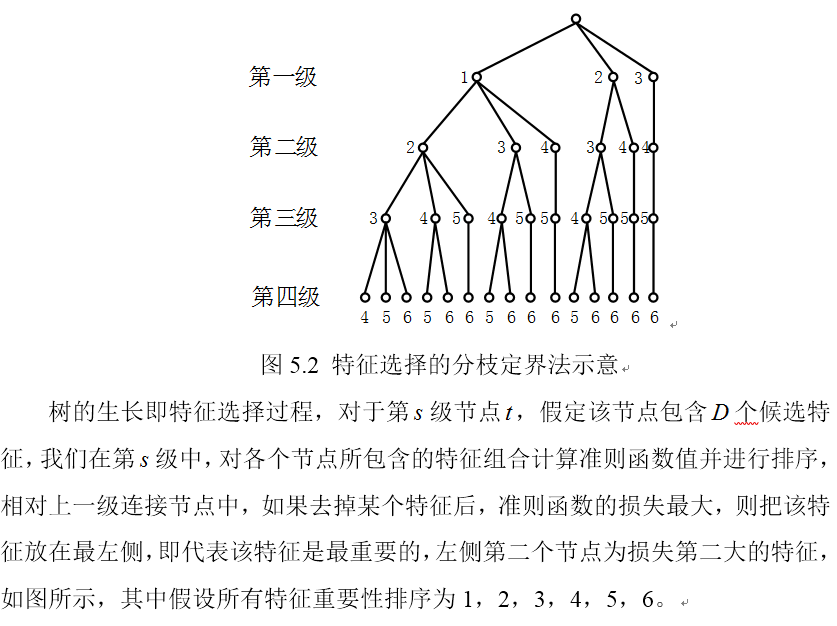
7、分枝定界算法


特征/特征子集评价
1、基于距离的评价
各类样本可以分开是因为它们位于特征空间的不同区域,显然这些区域之间距离越大,类别可分性就越大。现在我们考虑更为简单的准则上,这些准则考虑在一维空间中特征向量样本分布之间的关系。定义下列矩阵:



基于类内类间距离的可分离性判据是一种常用的判据,它实际上是各类向量之间的平均距离。具体而言,即 J(x) 表示各类特征向量之间的平均距离,我们通常认为 J(x) 越大,可分离性越好。这种判据优点是计算简单;缺点是当类间距离较小,类内距离较大时,判据仍有可能取得较大的值,而此时的可分离性并不大。
2、基于概率分布的评价准则
上面介绍的距离准则是直接从各类样本间的距离出发的,没有考虑各类的概率分布,不能确切表明各类交叠的情况,因此与错误概率没有直接联系,下面介绍一些基于概率分布的可分性判据。


3、基于熵的可分性判据
在信息论中,熵(Entropy)表示不确定性,熵越大不确定性越大,对随机变量来说也就是其包含的信息量越大。可以借用熵的概念来描述各类的可分性。如果将熵的概念应用在特征选择中,便能够帮助人们寻找到含有最多信息的特征,并成为一种好的全局测度。
假设数据集的属性皆为离散属性,这样给定一个特征子集,便可以通过这个特征子集的取值将数据集合划分为V个子集。例如:A1={男,女},A2={本科,硕士}就可以将原数据集划分为2*2=4个子集,其中每个子集的取值完全相同。这时我们就可以像决策树选择划分属性那样,通过计算信息增益来评价该属性子集的好坏。

一般的


4、基于最小冗余最大相关性的评价准则
实际应用中,单独的某几个特征对学习器的性能可能有很好的表现,但由于特征之间存在冗余,将这些特征组合在一起反而难以达到预期的效果。因此,在对特征进行评价时,除了考虑到选择到的特征对学习器性能的影响还应考虑到特征之间的冗余。这就是最小冗余最大相关性(MRMR)的由来。



5、基于分类正确率的评价准则
前面介绍的几种特征评价准则都使用分类器正确率之外的指标,这类不使用学习器性能作为评价准则的方法对应于特征选择中的过滤式方法。相对地,直接使用学习器性能作为评价准则,并在此基础上进行特性子集搜索后送入学习器训练的方法称为包裹式特征选择方法。
特征选择分类
特征选择算法根据其工作原理,主要分为过滤式(Filter)、包裹式(Wrapper)、嵌入式(Embedded)三大类。
1、过滤式
基于过滤的方法采用独立于分类器的评价准则函数作为指标来搜索最佳波段子集。先对数据集进行特征选择,然后再训练学习器以检验实际效果。也就是说特征选择的过程独立于后续的学习器训练过程。其优点是执行效率较高,但精度可能受限。
2、包裹式
包裹式的方法直接以学习器的精度作为衡量特征子集好坏的标准。因为选择到的特征是为学习器量身定做的,所以其得到的特征代表性强,最有利于该学习器。但其每进行一次特征子集搜索就要重新训练一遍学习器,需要巨大的计算代价。
3、嵌入式
前面提到了的两种特征选择方法:过滤式中特征选择与后续学习器完全分离,包裹式则是使用学习器作为特征选择的评价准则;嵌入式是一种将特征选择与学习器训练完全融合的特征选择方法,即将特征选择融入学习器的优化过程中。
经验风险指的是模型与训练数据的契合度,结构风险则是模型的复杂程度,机器学习的核心任务就是:在模型简单的基础上保证模型的契合度。例如:岭回归就是加上了L2范数的最小二乘法,有效地解决了奇异矩阵、过拟合等诸多问题,下面的嵌入式特征选择则是在损失函数后加上了L1范数。
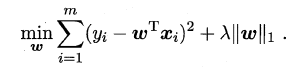
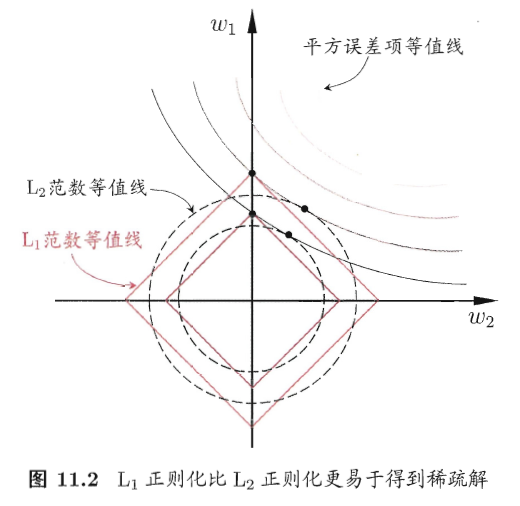
L1范数美名又约Lasso Regularization,指的是向量中每个元素的绝对值之和,这样在优化目标函数的过程中,就会使得w尽可能地小,在一定程度上起到了防止过拟合的作用,同时与L2范数(Ridge Regularization )不同的是,L1范数会使得部分w变为0, 从而达到了特征选择的效果。
总的来说:L1范数会趋向产生少量的特征,其他特征的权值都是0;L2会选择更多的特征,这些特征的权值都会接近于0。这样L1范数在特征选择上就十分有用,而L2范数则具备较强的控制过拟合能力。可以从下面两个方面来理解:
(1)下降速度:L1范数按照绝对值函数来下降,L2范数按照二次函数来下降。因此在0附近,L1范数的下降速度大于L2范数,故L1范数能很快地下降到0,而L2范数在0附近的下降速度非常慢,因此较大可能收敛在0的附近。
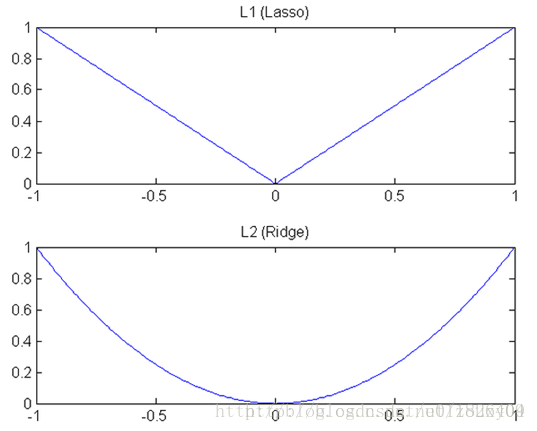
(2)空间限制:L1范数与L2范数都试图在最小化损失函数的同时,让权值W也尽可能地小。我们可以将原优化问题看做为下面的问题,即让后面的规则则都小于某个阈值。这样从图中可以看出:L1范数相比L2范数更容易得到稀疏解。