实验二 树
实验一
题目
参考教材p375,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
代码实现
在这部分最主要要实现的就是先序遍历和后序遍历的代码,而这两项最主要的就是补全BTNode类中的方法,在课本中有这么一段代码:``
public void inorder (ch16.ArrayIterator<T> iter)
{
if (left != null)
left.inorder (iter);
iter.add (element);
if (right != null)
right.inorder (iter);
}
是用来实现中序遍历的,而实现其他剩下的两个方法就是在这个基础上实现,只需要调节元素列表的顺序就可以了,先进列表在获取左子树就是先序,先获取左子树然后就进列表就是中序遍历,先获取左子树后获取右子树最后再进列表就可以了。
代码链接
截图
收获
这个小实验最主要的就是树的实现,在前一个周我们学习了有关树的知识点的学习,在这周就进行时间来加强应用的实践。上周博客
实验二
题目
基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能,比如教材P372,给出HDIBEMJNAFCKGL和ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
代码实现
实现之前先自己在巩固一下还原树的过程(参考)
int ai=0; // 声明一个数;
//确定根在数组中的位置
while(mid[ai]!=value)
ai++;
if (ai>0) {
//将左子树中的元素的先序表达式放入新的数组
Object[]leftSubPreOrder=new Object[ai];
for(int i=0;i<leftSubPreOrder.length;i++){
leftSubPreOrder[i]=pre[i+1];
}
//将左子树中的元素的先序表达式放入新的数组
Object[]leftMid=new Object[ai];
for(int i=0;i<leftMid.length;i++){
leftMid[i]=mid[i];
}
root.left=buildTree(leftSubPreOrder, leftMid);
}
代码已经加上了比较详细的解释,另外右子树的方法差不多,也就没有详细的介绍了;
代码链接
截图

实验三
题目
完成PP16.6
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
代码实现
第三个实验好像没有什么难点,最主要注意的就是建树的时候就应该注意建树的方法是要自底向上来建立树。还有就是设计问题的时候很费劲。
代码链接
截图

收获
这个问题就是树的直接的应用,很直观也很有代表性,可以让我们更好的使用树这个工具来去做更多的事;
实验四
题目
完成PP16.8
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
代码实现
在实现这段代码的时候我一直在思考优先级的问题,在建树的时候就要考虑优先级,还是在建树之后在计算的时候再考虑优先级的问题,原先我先进行了在建树的时候就考虑优先记的问题,但是在实现的过程中出现了很多问题,没有办法建树与优先级兼顾,所以我就不得不放弃了这一种做法,来就开始实现第二种思路,先建树再去考虑优先级的问题。首先我将建好的树换在草稿纸上,看要怎么计算,我在找资料的时候就找到了表达式树的遍历的规律,后序遍历就是表达式的后缀表达式,加上我们前个学期的结对编程完成的项目中就有后缀表达式计算,所以问题就解决了。
代码链接
截图
收获
主要的收获就是要学会代码的复用,我们已经写过的代码,要学会运用到之后的学习过程中,这样才能体现出我们的学习成果来;
实验五
题目
完成PP17.1
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
代码实现
public T findMin()throws ElementNotFoundException {
T min ;
// 获取最左边的也就是最小的元素
while (root.getLeft()!=null ){
root = root.getLeft();
}
min = root.getElement();
return min;
}
public T findMax()throws ElementNotFoundException {
T max ;
// 获取最右边的的也就是最大的元素
while (root.getRight()!=null ){
root = root.getRight();
}
max = root.getElement();
return max;
}
对于这两个方法的实现还算比较的顺利,这个方法这么简单的原因就是在建立树的时候就是有一定的规律,这个规律就决定了最小的树一定在左子树而最大的元素就在右子树中。下面这个图里就有一个比较好的例子。
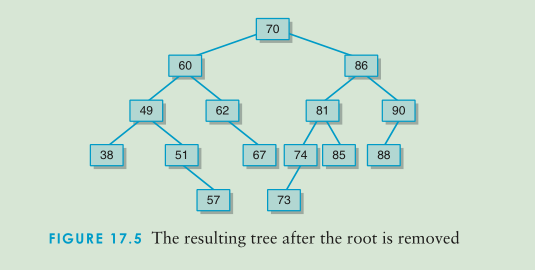
代码链接
截图
收获
实验六
题目
参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树(TreeMap,HashMap)进行源码分析,并在实验报告中体现分析结果
TreeMap
这个类里的方法很多,有的还比较复杂,我就挑了我们平时见得比较多的几个方法;
public boolean containsValue(Object value) {
for (Entry<K,V> e = getFirstEntry(); e != null; e = successor(e))
if (valEquals(value, e.value))
return true;
return false;
}
这个方法实现的看似很简单,但是他有调用了很多的方法;
public V remove(Object key) {
Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
/**
* Removes all of the mappings from this map.
* The map will be empty after this call returns.
*/
public void clear() {
modCount++;
size = 0;
root = null;
}
这是两删除操作的方法,代码的注释的详细值得我们去学习;
public V get(Object key) {
Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
这段代码的返回的值的方法自己还附带了一个判断,对java运算符的应用很棒。
HashMap
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
这个方法跟TreeMap中的get类有点像;
Node<K,V>[] tab; V v;
Entry<K,V> p = getEntry(key);
上面的两段代码分别来自两个类,这里的尖括号里的东西比较的陌生我并不知道它是什么。经过了解知道这是键值对(跟离散数学里的序偶有点相似)键:就是你存的值的编号
值:就是你要存放的数据,就是通过一个键来存取值,键可以是任何类型!
总之源码的简洁,与代码的方法的简便和对代码的复用,都值得我们学习。