20162324 2017-2018-1 《程序设计与数据结构》第7周学习总结
教材学习内容总结
本周主要学习的就是有关树的相关的知识点,在下面做个总结:
关键名词
树(tree)、节点(node)、边(edge)、子结点(children)、兄弟节点(sibling)、叶结点(leaf)、内部结点(internal node)、子树(subtree)、度(order)
- 树的分类
1.根据最大的子结点的个数进行分类。
2.看树是否平衡,如果所有子结点都在同一层上,或彼此最多不超出一层,则认为树是平衡的。
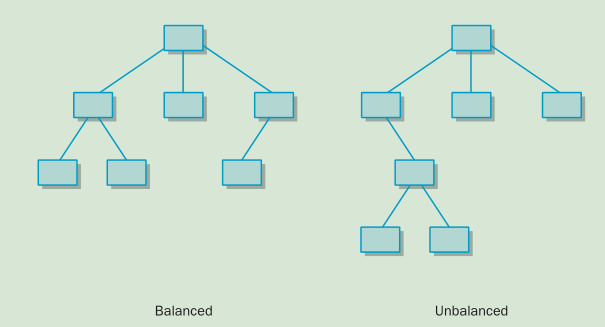
3.完全树和满树,如果树的所有的子结点都在同一层,并且每个非叶结点都正好有n个子结点,则称n叉树是满的。,如果树是满的,或一直到倒数第二层都是满的且最底层每个叶结点都在位于树的左侧,则称树是完全的(complete)
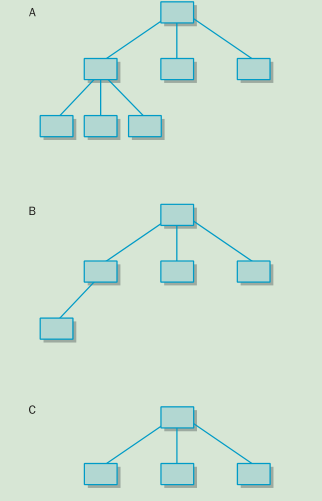
在上图中A、B是完全树但不是满树,C既是完全树也是满树。
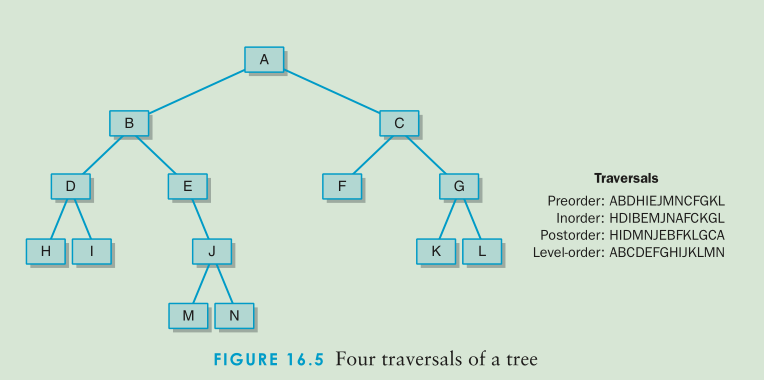
树的遍历
先序遍历:访问根,自左到右遍历子树。(DLR)
中序遍历: 遍历左子树,然后访问根,然后自左至右的遍历余下的各子树。(LDR)
后序遍历:自左至右的遍历各子树然后访问根。(LRD)
层序遍历: 从树的根到叶结点,从左至右,访问每一层的每一个结点。
实例:
二叉树的实现策略:
在实现之前我们需要了解二叉树的一些性质:

- 在数组中计算链
对于满树或完全二叉树通过特定的计算可以使用数组来表示。
在使用数组实现二叉树时,位置位于n的元素的左孩子在(2n+1)其右孩子在(2* (n +1))
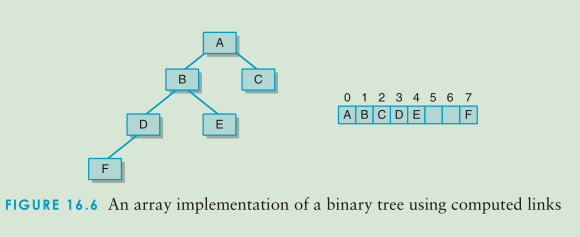
从图中就可看出虽然这种方式可以表示数,但是这种方法的空间的效率就很低,浪费了比较多的空间,从算法的效率的角度出发时不可行,所以我们需要寻找一种新的表示方法来使算法的空间效率更高。 - 在数组中保存链
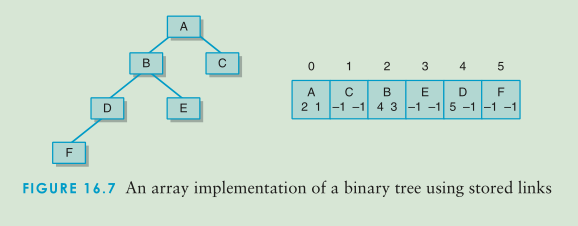
如上图:数组中的下面的数组就是表示他的左右孩子的位置A下面的2 1 表示左孩子在数组中的下标为2,右孩子的下标为1,如果出现的是-1表示这一侧没有孩子。
这个保存方法解决了在前一个问题中提到的空间效率的问题,但是鱼与熊掌不可兼得,它在对数组进行删除元素时的开销就变大了因为他要填补删除元素的空格,就需要移动余下的很多的元素。 - 链式结点
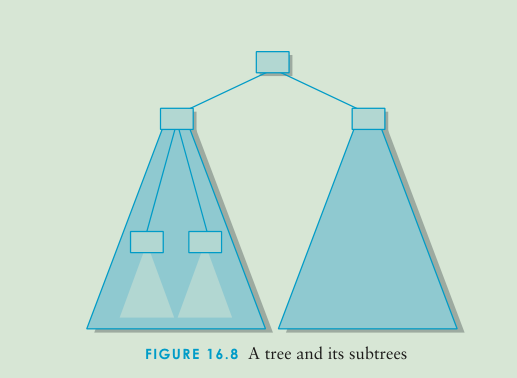
这个方法是将树看做是一个高度为2的树,又将左右子树进行相同的操作,这样的组织的方法有助于我们用递归的方法来解决问题
二叉树的实现
教材学习中的问题和解决过程
- 问题1:在课本上有一段代码
root.setLeft(left.root);
root.setRight(right.root);
在刚开始看这段代码的时候我我很不理解这段代码。为什么要在后面加上.root这一段代码。
- 问题1解决方案:当然看不懂时最好的办法就是在看,后来我发现了我才考虑到数据类型方面的问题,在方法中传入的类型:
public LinkedBinaryTree (T element, LinkedBinaryTree<T> left,LinkedBinaryTree<T> right)
而在setLeft和setRight方法中的参数又是另一种类型:
public void setLeft (BTNode<T> left)
{
this.left = left;
}
public BTNode<T> getRight()
{
return right;
}
所以就需要将类型转换,所以就有了这段奇怪的代码。
代码调试中的问题和解决过程
- 问题1:在打十六章的代码时发现少了一个ArrayIterator
类。 - 问题1解决方案:现在还没法解决
代码托管
上周考试错题总结

索引列表有一个数字索引,可以用来引用一个元素。 有序和无序列表没有索引。
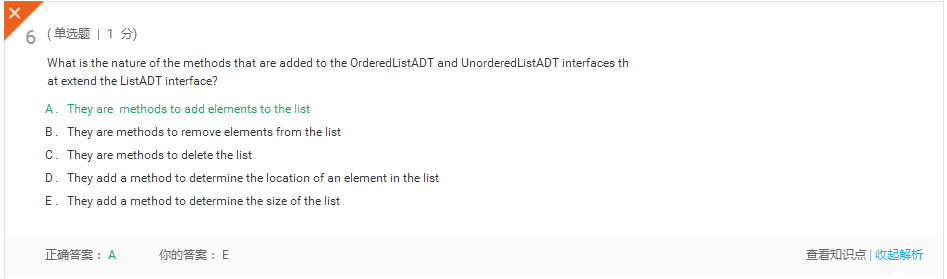
添加的方法是在OrderedlistATD接口定义。 的addtofront,addtorear,和addafter方法在unorderedlistATD接口定义。
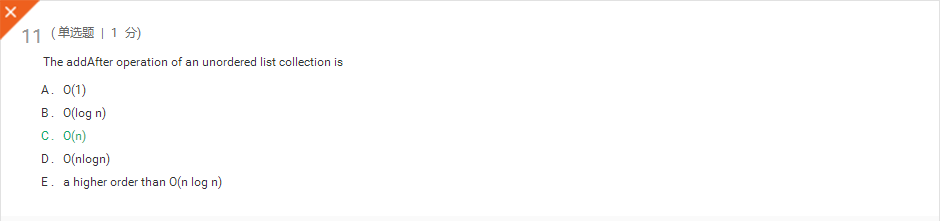
addafter操作使用两个参数,一个是参考元素添加另一个元素的引用,之前的位置的元素将被添加。 的addafter操作将要执行一个数量的比较来定位元素之前的位置的元素将被添加,随之而来的一些元素的位置移动,使添加的元素的房间后。 一起,和移动的比较使这是一个O(n)的操作。
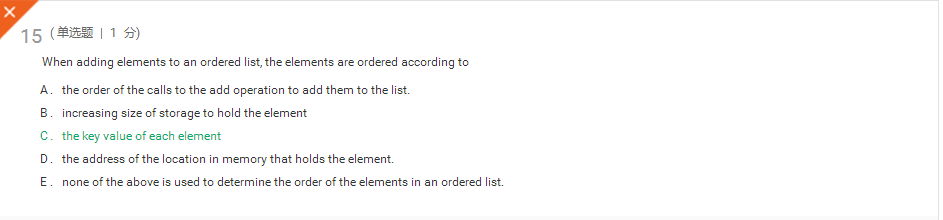
有序列表中的每个元素都有一个用于确定元素排序的特性。 这种特性称为核心价值。 作为一个元素添加到列表的元素的键的值进行比较的列表中已存在的元素的关键值直到元素的适当位置的确定。
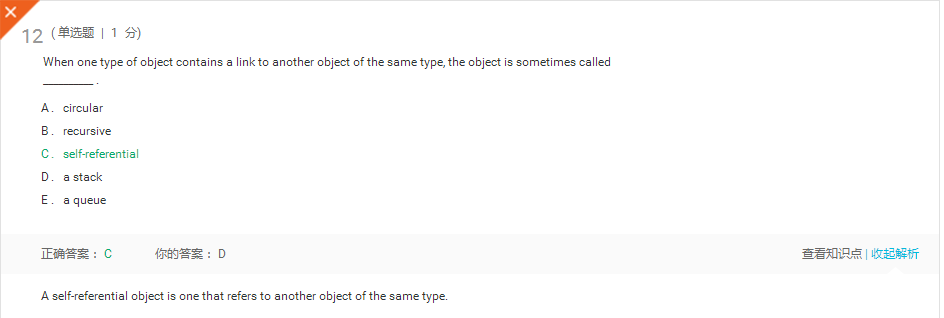
本周结对学习情况
- 20162312
- 结对照片
- 结对学习内容
- 有关队列的相关知识点。
- 有关树的知识点。
其他(感悟、思考等,可选)
这周过的比较的平淡没有发生什么事,没有了运动会的干扰生活回到了正轨,有条不紊。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 196/196 | 1/1 | 11/11 | 对于算法有了进一步的了解 |
| 第二周 | 76/270 | 1/2 | 10/21 | 了解一种新的方法,提高代码的复用性。 |
| 第三周 | 757/1027 | 2/4 | 10/31 | 了解很多的高效率的排序的方法和两种查找方法 |
| 第四、五、六 | 1768/2805 | 6/10 | 45/76 | 了解队列、栈等相关知识 |
| 第七周 | 1037 /3842 | 3/13 | 14/90 | 了解了非线性结构树 |
-
计划学习时间:18小时
-
实际学习时间:14小时
-
改进情况:
这周的时间安排我觉得还是很好的,没有出现太大的纰漏。