数据结构实验之二叉树一:树的同构
Problem Description
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。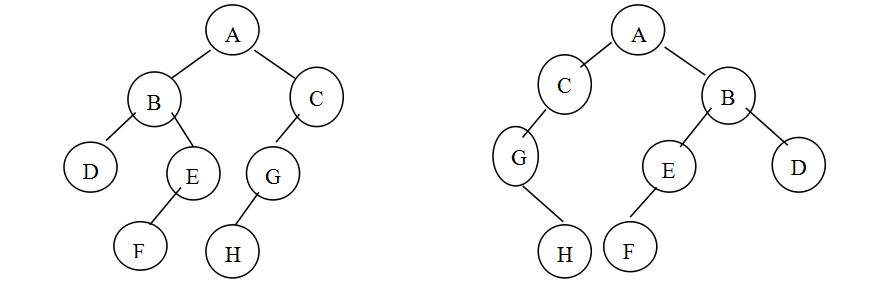
图1

图2
现给定两棵树,请你判断它们是否是同构的。
Input
注意:题目保证每个结点中存储的字母是不同的。
Output
Example Input
8 A 1 2 B 3 4 C 5 - D - - E 6 - G 7 - F - - H - - 8 G - 4 B 7 6 F - - A 5 1 H - - C 0 - D - - E 2 -
Example Output
Yes
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <malloc.h>
using namespace std;
typedef struct node
{
char data;
struct node *parent,*rchild,*lchild;
}tree;
typedef struct gp
{
int L,R;
tree *p;
}god; int i,n;
tree *creat(god *f)
{
for(i=0;i<n;i++)
{
if(f[i].L!='-')
{
f[i].p->lchild = f[f[i].L-48].p;
f[f[i].L-48].p->parent = f[i].p;
}
if(f[i].R!='-')
{
f[i].p->rchild = f[f[i].R-48].p;
f[f[i].R-48].p->parent = f[i].p;
}
}
for(i=0;i<n;i++)
{
if(f[i].p->parent==NULL) //双亲结点为空
{
return f[i].p;
}
}
return NULL;
}
bool justiceTree(tree *p1,tree *p2)
{
if(p1==NULL && p2==NULL)
{
return true;
}
else if(p1 == NULL || p2 == NULL)
{
return false;
}
if(p1->data!=p2->data)
{
return false;
}
if(
(justiceTree(p1->lchild,p2->lchild)&&justiceTree(p1->rchild,p2->rchild) )||
(justiceTree(p1->lchild,p2->rchild)&&justiceTree(p1->rchild,p2->lchild) )
)
return true;
return false;
}
int main()
{
god f[10086];
tree *root1,*root2;
char a[3],b[3],c[3];
while(scanf("%d",&n)!=EOF)
{
for(i=0;i<n;i++)
{
f[i].p = (tree *)malloc(sizeof(tree));
scanf("%s%s%s",a,b,c);
f[i].p->data = a[0];
f[i].L = b[0];
f[i].R = c[0];
f[i].p->parent = f[i].p->lchild = f[i].p->rchild = NULL;
}
root1 = creat(f);
scanf("%d",&n);
for(i=0;i<n;i++)
{
f[i].p = (tree *)malloc(sizeof(tree));
scanf("%s%s%s",a,b,c);
f[i].p->data = a[0];
f[i].L = b[0];
f[i].R = c[0];
f[i].p->parent = f[i].p->lchild = f[i].p->rchild = NULL;
}
root2 = creat(f);
if(justiceTree(root1,root2))
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
return 0;
}