线性回归的基本概念

线性回归的基本概念

线性回归是机器学习中最简单也是最重要的模型之一，其模型建立同样遵循上图流程：获取数据、数据预处理、训练模型、应用模型。

回归模型可以理解为：存在一个点集，用一条曲线去拟合它分布的过程。如果拟合曲线是一条直线，则称为线性回归。如果是一条二次曲线，则被称为二次回归。线性回归是回归模型中最简单的一种。

在线性回归中有几个基本的概念需要掌握：

假设函数（Hypothesis Function）
损失函数（Loss Function）
优化算法（Optimization Algorithm）

假设函数：
假设函数是指，用数学的方法描述自变量和因变量之间的关系，它们之间可以是一个线性函数或非线性函数。 在本次线性回顾模型中，我们的假设函数为 ，其中，$hat{Y} = aX_1 + b$表示模型的预测结果（预测房价），用来和真实的Y区分。模型要学习的参数即：a,b。

损失函数：
损失函数是指，用数学的方法衡量假设函数预测结果与真实值之间的误差。这个差距越小预测越准确，而算法的任务就是使这个差距越来越小。建立模型后，我们需要给模型一个优化目标，使得学到的参数能够让预测值$hat{Y}$ 尽可能地接近真实值Y。输入任意一个数据样本的目标值$y_i$和模型给出的预测值$hat{Y_i}$ ，损失函数输出一个非负的实值。这个实值通常用来反映模型误差的大小。

对于线性模型来讲，最常用的损失函数就是均方误差（Mean Squared Error， MSE）。 $MSE =frac{1}{n} sum_{i=1}^{n}(hat{Y_i}-Y_i)^2$

即对于一个大小为n的测试集，MSE是n个数据预测结果误差平方的均值。

优化算法：

在模型训练中优化算法也是至关重要的，它决定了一个模型的精度和运算速度。本章的线性回归实例中主要使用了梯度下降法进行优化。

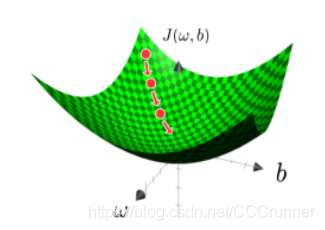
梯度下降是深度学习中非常重要的概念，值得庆幸的是它也十分容易理解。损失函数$J(w,b)$可以理解为变量$w$和$b$的函数。观察下图，垂直轴表示损失函数的值，两个水平轴分别表示变量$w$和$b$。实际上，可能是更高维的向量，但是为了方便说明，在这里假设$w$和$b$都是一个实数。算法的最终目标是找到损失函数的最小值。而这个寻找过程就是不断地微调变量$w$和$b$的值，一步一步地试出这个最小值。而试的方法就是沿着梯度方向逐步移动。本例中让图中的圆点表示损失函数的某个值，那么梯度下降就是让圆点沿着曲面下降，直到取到最小值或逼近最小值。

因为是凸函数，所以无论初始化在曲面上的哪一点，最终都会收敛到同一点或者相近的点。