[算法] 树链剖分解析

前置知识

线段树 (and) 树上基本操作

定义

几个在树链剖分很重要的概念。

重儿子

对于一个父节点，含有节点数最多的儿子称为重儿子。但重儿子只有一个，若满足条件的儿子有多个，则指定其中任意一个儿子为重儿子。

轻儿子

对于一个父节点，除了重儿子以为，其余的都称为轻儿子。

重边

由父节点与重儿子构成的边。

轻边

由父节点与轻儿子构成的边。

重链

由重边构成的链。

轻链

由轻边构成的链。

链顶

重链中深度最小的边为该重链的链顶。

上述几个概念具体如下图：

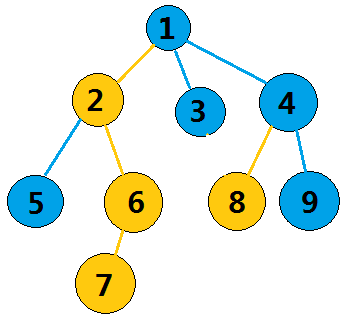
其中，黄色点为重儿子，蓝色点为轻儿子（ (1) 除外）。黄色边为重边，蓝色边为轻边。通常，一个单独的点也看为一条重链，那么重链有 (5) 条：

• ({ 1,2,6,7}) ，（ (1) 为链顶）
• ({ 5}) ，（ (5) 为链顶）
• ({ 3}) ，（ (3) 为链顶）
• ({ 4,8}) ，（ (4) 为链顶）
• ({ 9}) ，（ (9) 为链顶）

对于任意一棵树有如下性质：从任意一点到根节点的简单路径上，共有不超过 (log2(n)) 条轻链，有不超过 (log2(n)) 条轻链。

预处理

预处理需要使用到两个 (dfs) 。

(dfs1) 需要处理：

• (fa[i]) ： (i) 节点的父亲。
• (son[i]) ： (i) 节点的重儿子。
• (sz[i]) ：以 (i) 为根节点的子树的大小，可以进一步处理 (son[i]) 。
• (dep[i]) ： (i) 节点的深度。

(dfs2) 需要处理：

• (dfn[i]) ： (i) 节点的时间戳，但优先遍历重儿子。显然，在一条重链中，时间戳为一段连续的数字。
• (tp[i]) ： (i) 节点的链顶。

C++代码

void dfs1(int now, int father) {
	fa[now] = father;//初始化父节点
	sz[now] = 1;//子树大小包括自己
	dep[now] = dep[father] + 1;//初始化深度
	int SIZ = v[now].size();
	int maxn = 0;//记录最大的子树大小
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(next == father)
			continue;
		dfs1(next, now);//遍历这棵树
		sz[now] += sz[next];
		if(maxn < sz[next]) {//更新子节点
			maxn = sz[next];
			son[now] = next;
		}
	}
}
void dfs2(int now, int Top) {
	tp[now] = Top;//初始化链顶
	if(son[now])
		dfs2(son[now], Top);//优先遍历重儿子
	int SIZ = v[now].size();
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(next == fa[now] || next == son[now])
			continue;
		dfs2(next, next);//继续遍历这棵树
	}
}

树链剖分求LCA

测验链接。

在线查询一棵树上任意两点的 (LCA) 。

分两种情况向上爬即可（需要保证 (dep[tp[x]] <= dep[tp[y]])）：

1. (tp[x]!=tp[y]) ，即不在一条重链上。需要 (x) 向上爬出这条重链，向上继续寻找能与 (y) 汇合的重链点。(x=fa[tp[x]])。
2. (tp[x]!=tp[y]) ，即在一条重链上，那么深度小的就位最近公共祖先。

正确性显然，以为两条重链不会交于同一个点。

C++代码

#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 5e5 + 5;
vector<int> v[MAXN];//vector存图
int fa[MAXN], son[MAXN], tp[MAXN], sz[MAXN], dep[MAXN];
int n, m, s;
void dfs1(int now, int father) {//初始化如上
	fa[now] = father;
	sz[now] = 1;
	dep[now] = dep[father] + 1;
	int SIZ = v[now].size();
	int maxn = 0;
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(next == father)
			continue;
		dfs1(next, now);
		sz[now] += sz[next];
		if(maxn < sz[next]) {
			maxn = sz[next];
			son[now] = next;
		}
	}
}
void dfs2(int now, int Top) {//初始化如上
	tp[now] = Top;
	if(son[now])
		dfs2(son[now], Top);
	int SIZ = v[now].size();
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(next == fa[now] || next == son[now])
			continue;
		dfs2(next, next);
	}
}
int Get_LCA(int x, int y) {
	while(tp[x] != tp[y]) {
		if(dep[tp[x]] < dep[tp[y]])
			swap(x, y);
		x = fa[tp[x]];
	}
	if(x == y)
		return x;
	if(dep[x] < dep[y])
		return x;
	return y; 
}
int main() {
	int A, B;
	scanf("%d %d %d", &n, &m, &s);
	for(int i = 1; i < n; i++) {
		scanf("%d %d", &A, &B);
		v[A].push_back(B);
		v[B].push_back(A);
	}
	dfs1(s, 0);
	dfs2(s, s);
	for(int i = 1; i <= m; i++) {
		scanf("%d %d", &A, &B);
		printf("%d
", Get_LCA(A, B));
	}
	return 0;
}

例题

树链剖分通常结合着一些数据结构来进行操作，以为重链的 (dfn) 为连续的序列。

题目链接。

题目大意

对于一棵树，有 (5) 中操作，根据要求完成操作。

• C i w 将输入的第 (i) 条边权值改为 (w) 。
• N u v 将 (u,v) 节点之间的边权都变为相反数。
• SUM u v 询问 (u,v) 节点之间边权和。
• MAX u v 询问 (u,v) 节点之间边权最大值。
• MIN u v 询问 (u,v) 节点之间边权最小值。

思路

先考虑第二个操作。

设 (lca) 为 (u,v) 的最近公共祖先，那么可以将操作二分解为从 (u) 到 (lca) 的路径取反，和将从 (v) 到 (lca) 的路径取反。

那么按照上述 (LCA) 往上爬的过程刚好就可以遍历完这条路径一次。

按照点的 (dfn) 建造一颗线段树，来维护点的信息。

这里点的信息是指：这个点与它的父节点的连边的信息。

线段树需要维护的信息有：最大值，最小值，区间和。

具体的操作二代码如下：

void Negate(int pos, int l, int r) {
	if(l <= L(pos) && R(pos) <= r) {
		A(pos) = -A(pos);
		I(pos) = -I(pos);
		swap(A(pos), I(pos));//最大值取反，最小值取反，最大值边最小值
		S(pos) = -S(pos);//区间和取反
		M(pos) ^= 1;//取反两次后就相当于不取反。
		return;
	}
	Push_Down(pos);//传递懒标记
	if(l <= R(LC(pos)))
		Negate(LC(pos), l, r);
	if(r >= L(RC(pos)))
		Negate(RC(pos), l, r);
	Push_Up(pos);//修改后更新点的信息
}
void Negatepast(int x, int y) {
	while(tp[x] != tp[y]) {//不同重链向上爬
		if(dep[tp[x]] < dep[tp[y]])
			swap(x, y);
		Negate(1, dfn[tp[x]], dfn[x]);//同一条重链dfn是连续的，线段树维护
		x = fa[tp[x]];//向上爬
	}
	if(x == y)
		return;
	if(dep[x] < dep[y])
		swap(x, y);
	Negate(1, dfn[son[y]], dfn[x]);//注意是son[y]，y与其父节点的连边并不需要修改
}

查询操作与其类似，就不一一列举了。

对于修改权值，使用深度较大的子节点，直接在线段树上该就好了。

C++代码

#include <cstdio>
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
#define INF 0x3f3f3f3f
const int MAXN = 2e5 + 5;
struct Segment_Tree {//线段树
	int Left_Section, Right_Section;
	int Max_Data, Min_Data, Sum_Data, Lazy_Mark;
	#define LC(x) (x << 1)
	#define RC(x) (x << 1 | 1)
	#define L(x) Tree[x].Left_Section//左区间
	#define R(x) Tree[x].Right_Section//右区间
	#define I(x) Tree[x].Min_Data//区间最小值
	#define A(x) Tree[x].Max_Data//区间最大值
	#define S(x) Tree[x].Sum_Data//区间和
	#define M(x) Tree[x].Lazy_Mark//懒惰标记（延迟标记）
};
Segment_Tree Tree[MAXN << 2];
vector<int> v[MAXN];//vector存图
int fa[MAXN], son[MAXN], dep[MAXN], siz[MAXN];
int tp[MAXN], dfn[MAXN];
int s[MAXN], t[MAXN], w[MAXN];
int n, q;
int tim;
void Push_Up(int pos) {//更新节点信息
	A(pos) = max(A(LC(pos)), A(RC(pos)));
	I(pos) = min(I(LC(pos)), I(RC(pos)));
	S(pos) = S(LC(pos)) + S(RC(pos));
}
void Push_Down(int pos) {//传递懒标记
	if(M(pos)) {
		I(LC(pos)) = -I(LC(pos));
		A(LC(pos)) = -A(LC(pos));
		swap(I(LC(pos)), A(LC(pos)));
		S(LC(pos)) = -S(LC(pos));
		M(LC(pos)) ^= 1;
		I(RC(pos)) = -I(RC(pos));
		A(RC(pos)) = -A(RC(pos));
		swap(I(RC(pos)), A(RC(pos)));
		S(RC(pos)) = -S(RC(pos));
		M(RC(pos)) ^= 1;
		M(pos) = 0;
	}
}
void Build(int pos, int l, int r) {//初始化建树
	L(pos) = l;
	R(pos) = r;
	if(l == r)
		return;
	int mid = (l + r) >> 1;
	Build(LC(pos), l, mid);
	Build(RC(pos), mid + 1, r); 
}
void Negate(int pos, int l, int r) {//取反操作
	if(l <= L(pos) && R(pos) <= r) {
		I(pos) = -I(pos);
		A(pos) = -A(pos);
		swap(I(pos), A(pos));
		S(pos) = -S(pos);
		M(pos) ^= 1;
		return;
	}
	Push_Down(pos);
	if(l <= R(LC(pos)))
		Negate(LC(pos), l, r);
	if(r >= L(RC(pos)))
		Negate(RC(pos), l, r);
	Push_Up(pos);
}
void Negatepast(int x, int y) {
	while(tp[x] != tp[y]) {
		if(dep[tp[x]] < dep[tp[y]])
			swap(x, y);
		Negate(1, dfn[tp[x]], dfn[x]);
		x = fa[tp[x]];
	}
	if(x == y)
		return;
	if(dep[x] < dep[y])
		swap(x, y);
	Negate(1, dfn[son[y]], dfn[x]);
}
void Change(int pos, int x, int c) {//单点修改
	if(L(pos) == R(pos)) {
		I(pos) = c;
		A(pos) = c;
		S(pos) = c;
		return;
	}
	Push_Down(pos);
	if(x <= R(LC(pos)))
		Change(LC(pos), x, c);
	else
		Change(RC(pos), x, c);
	Push_Up(pos);
}
int Query_Sum(int pos, int l, int r) {//查询最大值操作，与修改类似，都已同样方向爬
	if(l <= L(pos) && R(pos) <= r)
		return S(pos);
	Push_Down(pos);
	int res = 0;
	if(l <= R(LC(pos)))
		res += Query_Sum(LC(pos), l, r);
	if(r >= L(RC(pos)))
		res += Query_Sum(RC(pos), l, r);
	return res;
}
int Sumpast(int x, int y) {
	int res = 0;
	while(tp[x] != tp[y]) {
		if(dep[tp[x]] < dep[tp[y]])
			swap(x, y);
		res += Query_Sum(1, dfn[tp[x]], dfn[x]);
		x = fa[tp[x]];
	}
	if(x == y)
		return res;
	if(dep[x] < dep[y])
		swap(x, y);
	res += Query_Sum(1, dfn[son[y]], dfn[x]);
	return res;
}
int Query_Min(int pos, int l, int r) {//查询最小值
	if(l <= L(pos) && R(pos) <= r)
		return I(pos);
	Push_Down(pos);
	int res = INF;
	if(l <= R(LC(pos)))
		res = min(res, Query_Min(LC(pos), l, r));
	if(r >= L(RC(pos)))
		res = min(res, Query_Min(RC(pos), l, r));
	return res;
}
int Minpast(int x, int y) {
	int res = INF;
	while(tp[x] != tp[y]) {
		if(dep[tp[x]] < dep[tp[y]])
			swap(x, y);
		res = min(res, Query_Min(1, dfn[tp[x]], dfn[x]));
		x = fa[tp[x]];
	}
	if(x == y)
		return res;
	if(dep[x] < dep[y])
		swap(x, y);
	res = min(res, Query_Min(1, dfn[son[y]], dfn[x]));
	return res;
}
int Query_Max(int pos, int l, int r) {//查询最大值
	if(l <= L(pos) && R(pos) <= r)
		return A(pos);
	Push_Down(pos);
	int res = -INF;
	if(l <= R(LC(pos)))
		res = max(res, Query_Max(LC(pos), l, r));
	if(r >= L(RC(pos)))
		res = max(res, Query_Max(RC(pos), l, r));
	return res;
}
int Maxpast(int x, int y) {
	int res = -INF;
	while(tp[x] != tp[y]) {
		if(dep[tp[x]] < dep[tp[y]])
			swap(x, y);
		res = max(res, Query_Max(1, dfn[tp[x]], dfn[x]));
		x = fa[tp[x]];
	}
	if(x == y)
		return res;
	if(dep[x] < dep[y])
		swap(x, y);
	res = max(res, Query_Max(1, dfn[son[y]], dfn[x]));
	return res;
}
void dfs1(int now, int father) {//初始化
	dep[now] = dep[father] + 1;
	siz[now] = 1;
	fa[now] = father;
	int SIZ = v[now].size();
	int maxn = 0;
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(next == fa[now])
			continue;
		dfs1(next, now);
		siz[now] += siz[next];
		if(maxn < siz[next]) {
			maxn = siz[next];
			son[now] = next;
		}
	}
}
void dfs2(int now, int Top) {//初始化
	tp[now] = Top;
	dfn[now] = ++tim;
	if(son[now])
		dfs2(son[now], Top);
	int SIZ = v[now].size();
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(son[now] == next || fa[now] == next)
			continue;
		dfs2(next, next);
	}
}
int main() {
	scanf("%d", &n);
	for(int i = 1; i < n; i++) {
		scanf("%d %d %d", &s[i], &t[i], &w[i]);
		s[i]++;
		t[i]++;
		v[s[i]].push_back(t[i]);
		v[t[i]].push_back(s[i]);
	}
	dfs1(1, 0);
	dfs2(1, 1);
	Build(1, 1, n);
	for(int i = 1; i < n; i++) {
		if(dep[s[i]] < dep[t[i]])//深度小的一定就是子节点
			swap(s[i], t[i]);
		Change(1, dfn[s[i]], w[i]);//初始化线段树
	}
	scanf("%d", &q);
	string opt;
	int a, b;
	while(q--) {
		cin >> opt;
		scanf("%d %d", &a, &b);
		a++;
		b++;
		if(opt[0] == 'N')
			Negatepast(a, b);
		else if(opt[0] == 'C')
			Change(1, dfn[s[a - 1]], b - 1);
		else if(opt[0] == 'S')
			printf("%d
", Sumpast(a, b));
		else if(opt[1] == 'A')
			printf("%d
", Maxpast(a, b));
		else
			printf("%d
", Minpast(a, b));
	}
	return 0;
}