[算法] 缩点Tarjan算法解析

（注：我在网上找了一些图，希望原博主不要在意，谢谢，(｡☉౪ ⊙｡)）

首先来了解什么是强连通分量

有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

——摘自度娘

举个栗子：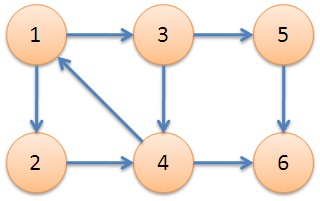

在下图中，{1，2，3，4}这4个点中，任意两点之间都可以到达。可以发现只要加入{1，2，3，4}这个集合中加入5，6任意两点，都满足不了任意两点之间都可以到达这个条件，所以不能构成强连通分量。而{5}，{6}就只单独算作两个强连通分量。所以这个图可分为3个强连通分量：{1，2，3，4}，{5}，{6}。

缩点Tarjan算法就是求出所有尽可能大的强连通分量的集合

我们定义几个变量：dfn（时间戳），low（该集合中最早遍历到的点的时间戳），s（正在访问的结点集合，用栈的方式存储），belong（当前结点属于的强连通分量的序数），elem（当前集合中元素的个数），instack（当前结点是否存在正在访问的栈中）。
可以通过定义得到：
low的初始值为该节点的时间戳。
即是：low[now]=dfn[now]。
若当前结点now的所连结点next正在被访问，则low[now]=min(low[now],dfn[next])。
若当前结点now的所连结点next未被访问，则low[now]=min(low[now],low[next])。
可以发现：
若low[now]=dfn[now]。
则正在访问的结点now与上一结点连接会形成一个环，环内元素为now与now相连的所有的结点。

---

实现过程：

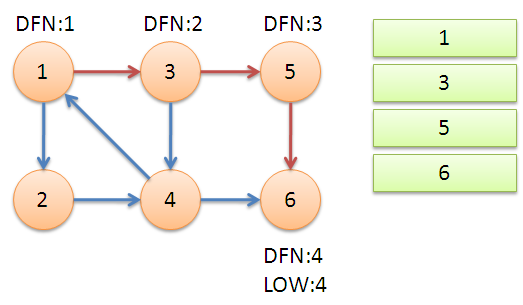
从1号结点开始搜索，一直搜到6的时候，再也没有路了，此时，low[now]=dfn[now]，而栈顶元素就是6，所以{6}就是此图的强连通量之一。

---

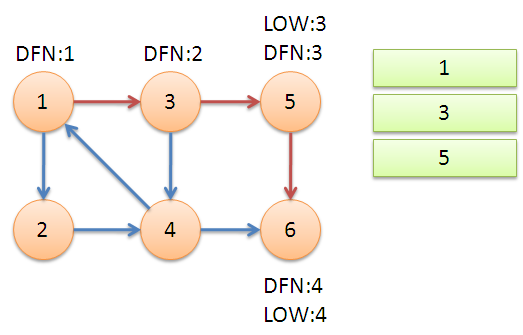
6出栈后，栈顶元素为5，对于5进行上图中6的操作，可发现{5}为一个强连通分量

---

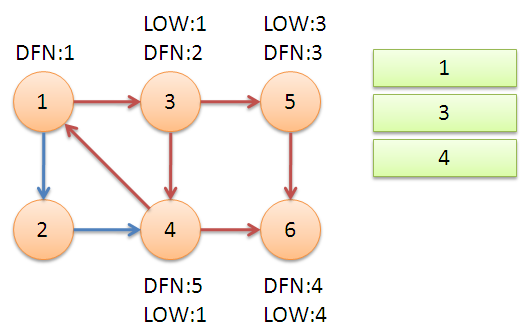
5出栈，对于3的另一条连边4进行标记，即4进栈

---

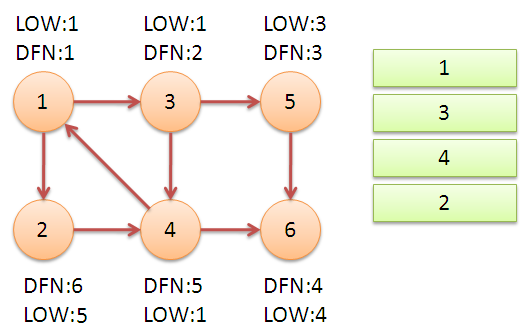
最后对于1的连边2进行标记。回溯后发现：dfn[1]=low[1]，从栈顶2到栈的最后一个元素1为一个强连通分量。存储{1，2，3，4}这个强连通分量。

---

C++实现：

void Tarjan(int now) {
	low[now] = dfn[now] = ++tim;
	instack[now] = true;
	s.push(now);
	int SIZ = v[now].size();
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(!dfn[next]) {
			Tarjan(next);
			low[now] = min(low[now], low[next]);
		}
		else if(instack[next])
			low[now] = min(low[now], dfn[next]);
	}
	if(dfn[now] == low[now]) {
		cnt_set += 1;
		int Top = -1;
		while(!s.empty() && Top != now) {
			elem[cnt_set]++;
			Top = s.top();
			belong[Top] = cnt_set;
			instack[Top] = false;
			s.pop();
		}
	}
}

结合这道题再来理解

题目TP门

题目描述

每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 A 喜欢 B，B 喜欢C，那么 A 也喜欢 C。牛栏里共有 N 头奶牛，给定一些奶牛之间的爱慕关系，请你算出有多少头奶牛可以当明星。

输入格式

第一行：两个用空格分开的整数：N 和 M。

接下来 M 行：每行两个用空格分开的整数：A 和 B，表示 A 喜欢 B。

输出格式

一行单独一个整数，表示明星奶牛的数量。

输入输出样例

输入

3 3
1 2
2 1
2 3

输出

1

说明/提示

只有 3 号奶牛可以做明星。

思路

首先考虑一个简单的问题：若该图是一个有向无环图，则必有一个点的出度为0。若还存在一个点出度也为0，则本题无解（较为简单就不证了）。
但是，现实是残酷的。
这张图中可能存在环，所以先用Tarjan缩点，将该图转换为有向无环图。在把该图当做上述情况求解即可。

C++代码

#include <stack>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 1e4 + 5;
vector<int> v[MAXN];
stack<int> s;
int dfn[MAXN], low[MAXN], belong[MAXN], elem[MAXN];
bool instack[MAXN];
int tim, cnt_set;
int out[MAXN];
int n, m, ans;
void Read();
void Tarjan(int);
void Build();
void Count();
int main() {
   Read();
   Build();
   Count();
   return 0;
}
void Count() {
   for(int i = 1; i <= n; i++) {
   	int SIZ = v[i].size();
   	for(int j = 0; j < SIZ; j++) {
   		int next = v[i][j];
   		if(belong[i] != belong[next])
   			out[belong[i]]++;
   	}
   }
   for(int i = 1; i <= cnt_set; i++) {
   	if(!out[i]) {
   		if(!ans)
   			ans = i;
   		else {
   			ans = 0;
   			break;
   		}
   	}
   }
   printf("%d", elem[ans]);
}
void Build() {
   for(int i = 1; i <= n; i++)
   	if(!dfn[i])
   		Tarjan(i);
}
void Tarjan(int now) {
   low[now] = dfn[now] = ++tim;
   instack[now] = true;
   s.push(now);
   int SIZ = v[now].size();
   for(int i = 0; i < SIZ; i++) {
   	int next = v[now][i];
   	if(!dfn[next]) {
   		Tarjan(next);
   		low[now] = min(low[now], low[next]);
   	}
   	else if(instack[next])
   		low[now] = min(low[now], dfn[next]);
   }
   if(dfn[now] == low[now]) {
   	cnt_set += 1;
   	int Top = -1;
   	while(!s.empty() && Top != now) {
   		elem[cnt_set]++;
   		Top = s.top();
   		belong[Top] = cnt_set;
   		instack[Top] = false;
   		s.pop();
   	}
   }
}
void Read() {
   scanf("%d %d", &n, &m);
   for(int i = 1; i <= m; i++) {
   	int A, B;
   	scanf("%d %d", &A, &B);
   	v[A].push_back(B);
   }
}