一、题目
二、解法
建立原图的 \(\tt dfs\) 树,分树边和非树边考察连通性。设删边集合是 \(P\),设覆盖树边 \(e\) 的非树边构成集合 \(S_e\),特别地,对于非树边 \(e\) 令 \(S_e=\{e\}\),有结论:
- 删边后图不连通等价于,\(\exist Q\not=\varnothing,Q\subseteq P,\Delta_{e\in Q} S_e=\varnothing\)(其中 \(\Delta\) 代表对称差,即集合异或)
必要性:对于一个极小的割边集合 \(Q\) 证明 \(\Delta _{e\in Q} S_e=\varnothing\) 即可。由于 \(Q\) 是割且 \(Q\) 极小,那么删去 \(Q\) 后图一定被分为两个联通块,对于与根不再联通的连通块,把它缩成一个点来考虑:
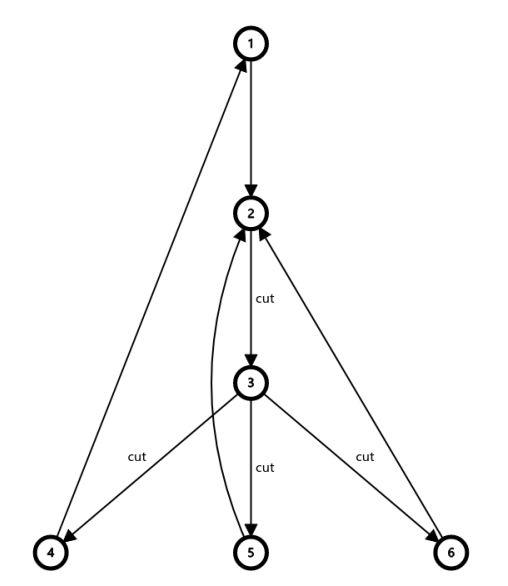
其中 \(3\) 是与根不再联通的连通块,那么对于 \(3\) 子树内未被删除的非树边,一定连向了 \(3\) 的一个严格祖先。那么它恰好经过了两条割边,被异或上了两次所以贡献为 \(0\);对于 \(3\) 子树内被删除了的树边,一定恰好经过一条割边,由于其自身需要贡献一次,所以贡献也为 \(0\)
充分性:对于满足 \(\Delta_{e\in Q} S_e=\varnothing\) 的集合 \(Q\) 证明它是割即可。至少会有一条树边 \(e_0\in Q\),那么被删除的树边会把原树划分为若干个连通块,我们把每个连通块缩成一个点,再用这些被删除的树边重构。考虑加入未被删除的非树边,如果把树黑白染色,那么这些非树边只会连接同色点,最后黑点和白点之间一定不连通,所以 \(Q\) 是割。
知道这个结论后,给每条非树边赋一个随机权值,对每条树边求出对应的权值,然后用线性基就可以判断这个条件了,时间复杂度 \(O(m+kq\log V)\)
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
using namespace std;
const int M = 1000005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,tot=1,Ind,f[M],w[M],a[M],b[32],id[M];
struct edge{int v,next;}e[M];
void dfs(int u,int fa)
{
id[u]=++Ind;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa) continue;
if(!id[v])
dfs(v,u),a[u]^=a[v],w[i>>1]=a[v];
else if(id[u]>id[v])
w[i>>1]=rand(),a[u]^=w[i>>1],a[v]^=w[i>>1];
}
}
int main()
{
n=read();m=read();srand(19260817);
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
e[++tot]=edge{v,f[u]},f[u]=tot;
e[++tot]=edge{u,f[v]},f[v]=tot;
}
dfs(1,0);
for(int t=0,q=read();q--;)
{
int k=read(),f=1;
memset(b,0,sizeof b);
while(k--)
{
int z=read()^t,x=w[z],F=0;
if(!f) continue;
for(int i=30;i>=0;i--) if(x>>i&1)
{
if(b[i]) x^=b[i];
else {b[i]=x;F=1;break;}
}
f&=F;
}
t+=f;
puts(f?"Connected":"Disconnected");
}
}