总结
这签到构造题我做不出也没有办法啊(...)
还是感谢 ( t Oneindark) 大佬的供题,希望她以后不要再出阴间构造题啦!
Ciel and Flipboard
题目描述
解法
我是这样打爆搜的,枚举左上角 (m imes m) 个元素的状态,那么整个矩阵的状态是唯一确定的。因为操作矩阵个数也是 (m imes m) 个,我们可以知道它们是线性不相关的。
下一个结论就比较难观察出来了,因为长度是 (m=frac{n+1}{2}) 很特殊,设 (s(x,y)) 表示位置 ((x,y)) 的符号位,如果是 (1) 我们设置成 (0),如果是 (-1) 我们设置成 (1),可以发现:
对这两个式子更深的理解就是当我们确定了"中线"以后,两边的符号位就是对应的。
( t Rainybunny) 通过打表发现了这个结论,这种符号位问题通常存在特殊结论哦~~
那么我们枚举 (s(m,i),ileq m),这时候 (m) 这一整行都能够确定,然后发现每一行是互相独立的,对于每一行单独做,我们先枚举中间点,然后枚举左上角的点,这时候四个点都确定了:
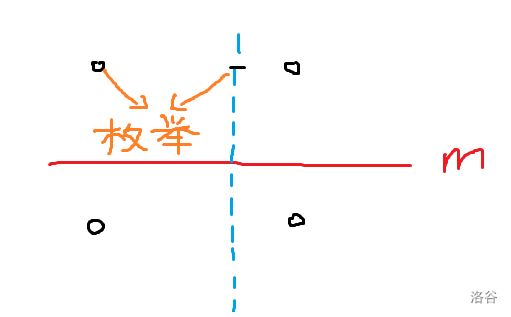
那么疯狂取最大值就行了,时间复杂度 (O(2^mm^2))
总结
想办法把变量独立起来,然后分别去最值,你可能需要枚举一些关键变量。
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 50;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,ans,a[M][M];
int val(int x,int y)
{
return x==0?y:-y;
}
int check(int S)
{
int o=S>>m-1,res=0;
for(int i=1;i<=m;i++)
res+=val((S>>i-1)&1,a[m][i]);
for(int i=m+1;i<=n;i++)
res+=val(o^((S>>i-m-1)&1),a[m][i]);
for(int i=1;i<m;i++)
{
int mx=-(1ll<<60);
for(int p=0;p<2;p++)
{
int s=val(p,a[i][m])+val(o^p,a[i+m][m]);
for(int j=1;j<m;j++)
{
int x=a[i][j]+val(p,a[i][m+j])
+val((S>>j-1)&1,a[m+i][j])
+val(((S>>j-1)&1)^o^p,a[i+m][j+m]);
if(x<0) x=-x;s+=x;
}
mx=max(mx,s);
}
res+=mx;
}
return res;
}
signed main()
{
//freopen("taozi.in","r",stdin);
//freopen("taozi.out","w",stdout);
n=read();m=(n+1)/2;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=read();
for(int i=0;i<(1<<m);i++)
ans=max(ans,check(i));
printf("%lld
",ans);
}
Shifting Dominoes
题目描述
解法
考虑两个空格的独立性,首先我们可以把矩阵黑白染色,那么空格初始颜色就不同,并且每次都是把平移两格,所以颜色是不会变的,这提示黑色格和白色格可以分开处理。
那么对于一个空格我们想求出它能到达的点,可以用图论表示这个过程,具体来说我们这样连边:
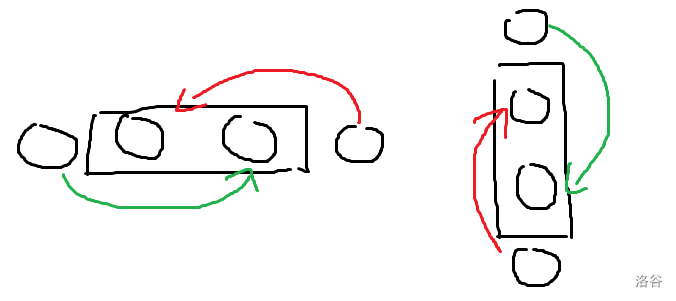
这个边就代表了空格能够沿着边的方向转移,不难发现每个点的入度至多为 (1),所以这是可以基环外向树,你可以通过反证如果构成环内部点数为奇数来说明不会有环,所以我们得到了一个树形结构。
那么一个空格能到达的位置对应着树上的一个子树,我们可以把它表示成一个 ( t dfn) 序区间,综合考虑两维就变成了一个矩形求并问题,用扫描线解决即可,时间复杂度 (O(nmlog nm))
总结
多个对象的问题可以找独立性来转化成单个对象的问题。
遇到奇怪的问题可以多想想图论,基本的分析还是要有。
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 200005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,t,Ind,p[M][2],cl[M],rt[M],di[M],dt[M];
vector<int> g[M];char s[M];long long ans;
struct node
{
int x,l,r,f;
bool operator < (const node &b) const
{
return x<b.x;
}
}q[M];
int id(int x,int y)
{
return (x-1)*m+y;
}
void add(int x,int y,int a,int b)
{
g[id(x,y)].push_back(id(a,b));
rt[id(a,b)]=1;
}
void dfs(int u)
{
di[u]=++Ind;
for(auto v:g[u])
if(!di[v]) dfs(v);
dt[u]=Ind;
}
int mi[4*M],num[4*M],tag[4*M];
void upd(int i,int c)
{
tag[i]+=c;
mi[i]+=c;
}
void down(int i)
{
if(!tag[i]) return ;
upd(i<<1,tag[i]);
upd(i<<1|1,tag[i]);
tag[i]=0;
}
void build(int i,int l,int r)
{
num[i]=r-l+1;mi[i]=0;
if(l==r) return ;
int mid=(l+r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
}
void add(int i,int l,int r,int L,int R,int f)
{
if(L>r || l>R) return ;
if(L<=l && r<=R)
{
upd(i,f);
return ;
}
int mid=(l+r)>>1;down(i);
add(i<<1,l,mid,L,R,f);
add(i<<1|1,mid+1,r,L,R,f);
mi[i]=min(mi[i<<1],mi[i<<1|1]);num[i]=0;
if(mi[i]==mi[i<<1]) num[i]=num[i<<1];
if(mi[i]==mi[i<<1|1]) num[i]+=num[i<<1|1];
}
int main()
{
//freopen("domino.in","r",stdin);
//freopen("domino.out","w",stdout);
n=read();m=read();
//build the graph
for(int i=1;i<=n;i++)
{
scanf("%s",s+1);
for(int j=1;j<=m;j++)
{
cl[id(i,j)]=(i+j)&1;
if(s[j]=='L' && j+2<=m)
add(i,j+2,i,j);
if(s[j]=='R' && j-2>=1)
add(i,j-2,i,j);
if(s[j]=='U' && i+2<=n)
add(i+2,j,i,j);
if(s[j]=='D' && i-2>=1)
add(i-2,j,i,j);
if(s[j]=='L' || s[j]=='U')
{
++k;p[k][0]=id(i,j);
if(s[j]=='L') p[k][1]=id(i,j+1);
if(s[j]=='U') p[k][1]=id(i+1,j);
}
}
}
for(int i=1;i<=n*m;i++)
if(!rt[i]) dfs(i);
for(int i=1;i<=k;i++)
{
int x=p[i][0],y=p[i][1];
if(cl[x]) swap(x,y);
q[++t]=node{di[x],di[y],dt[y],1};
q[++t]=node{dt[x]+1,di[y],dt[y],-1};
}
//scaning line
sort(q+1,q+1+t);k=n*m;
build(1,1,k);
for(int i=1,j=1;i<=k;i++)
{
while(j<=t && q[j].x<=i)
{
add(1,1,k,q[j].l,q[j].r,q[j].f);
j++;
}
ans+=k-(mi[1]==0?num[1]:0);
}
printf("%lld
",ans);
}