一、题目
二、解法
精妙的转化,我只是想说这种东西怎么可能训练得来嘛,这完全就是靠天赋啊...
树
先从这种简单的情况入手,考虑间隔染色,我们把奇数深度的点染成黑色,偶数深度的点染成红色,那么问题转化成了把所有原来为黑的点变成红色,原来为红的点变成黑色,每次可以交换两个点的颜色。
考虑构造答案下界,设某个子树有 (a) 个黑点、(b) 个红点,因为最终状态是 (b) 个黑点、(a) 个红点,那么父边至少交换 (|a-b|) 次。又因为每次一定能找到合法的交换点对(留读者自证),所以答案下界可以取到。
那么把黑点权值设为 (1),红点权值设为 (-1),设 (a_i) 表示 (i) 子树内的权值和,答案是 (sum |a_i|)
偶环树
受到树讨论的启发,考虑权值的变化即可。
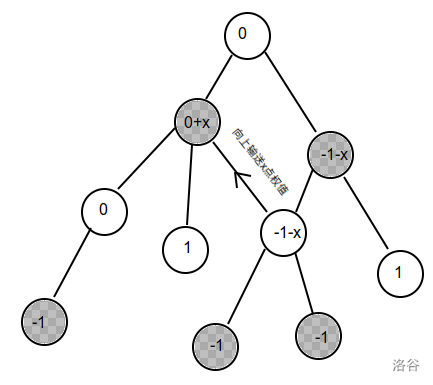
多出来这条边的作用其实就是把权值输送到另一个子树去,设输送的权值为 (x),那么左边的点权值就会增加 (x),右边的点权值就会减少 (x),记 (k_i) 为 (-1/1) 表示这个点的权值是增加还是减少,那么重新计算环上的交换次数是:
[sum|k_icdot a_i-x|+|x|
]
最小化这个式子直接取中位数即可。
奇环树
注意此种情况特殊边的作用就不是交换两个点的颜色了,而是把两个点的颜色直接反转(如果都是黑那么变成都是红、如果都是红那么变成都是黑),所以此种情况 (a_1) 是偶数既有解。
那么此条边使用的下界任然是 (frac{a_1}{2}),还是在适当时机交换即可(读者自证),考虑这条边的影响之后当树做就行了。
三、总结
本题运用的转化:同色操作转异色操作,可以去掉同色操作的限制。
#include <cstdio>
#include <algorithm>
using namespace std;
const int M = 100005;
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,sum,tot,f[M],a[M],w[M],st[M],A,B;ll ans;
struct edge
{
int v,next;
}e[2*M];
int Abs(int x)
{
return x>0?x:-x;
}
void dfs(int u,int fa)
{
sum+=w[u];
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(w[v] && v^fa)
A=u,B=v;
if(!w[v])
w[v]=-w[u],dfs(v,u);
}
}
void cal(int u,int fa)
{
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa || (u==A && v==B) || (u==B && v==A))
continue;
cal(v,u);
a[u]+=a[v];w[u]+=w[v];
}
}
int main()
{
n=read();m=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
e[++tot]=edge{v,f[u]},f[u]=tot;
e[++tot]=edge{u,f[v]},f[v]=tot;
}
w[1]=1;dfs(1,0);
if(sum%2) {puts("-1");return 0;}
if(A)
{
if(w[A]==w[B])//odd circle
{
ans+=Abs(sum)/2;
w[A]-=sum/2;w[B]-=sum/2;
sum=0;
}
else
a[A]++,a[B]--;
}
if(sum) {puts("-1");return 0;}
cal(1,0);st[++k]=0;
for(int i=1;i<=n;i++)
{
if(a[i]) st[++k]=a[i]*w[i];
else if(w[i]) ans+=Abs(w[i]);
}
sort(st+1,st+1+k);
int x=st[(k+1)/2];
for(int i=1;i<=k;i++)
ans+=Abs(st[i]-x);
printf("%lld
",ans);
}