Codeforces Round #703 (Div. 2)

C. Guessing the Greatest

题目描述

点此看题

解法

一开始只想到了傻逼二分，需要 (40) 次。

我们可以先找到全局的次大值的位置 (p)，问一次就可以知道最大值在他的哪一边。假设最大值在右边，那么问 ([p,r]) 的返回值如果是 (p) 就可知最大值在此区间内，利用可以性质可以 (20) 次以内倍增出答案。

那么为什么一开始的思路不行，因为没有全局的思维

F. Pairs of Paths

题目描述

点此看题

给定 (n) 个点的树，(m) 条简单路径，求有且仅有一个公共点的路径对数。

(1leq n,mleq 300000)

解法

好题，如果你不好好讨论的话很容易头就昏了。

首先考虑相交的两个路径是什么样子，手玩发现有这两种情况（嫖的图）：

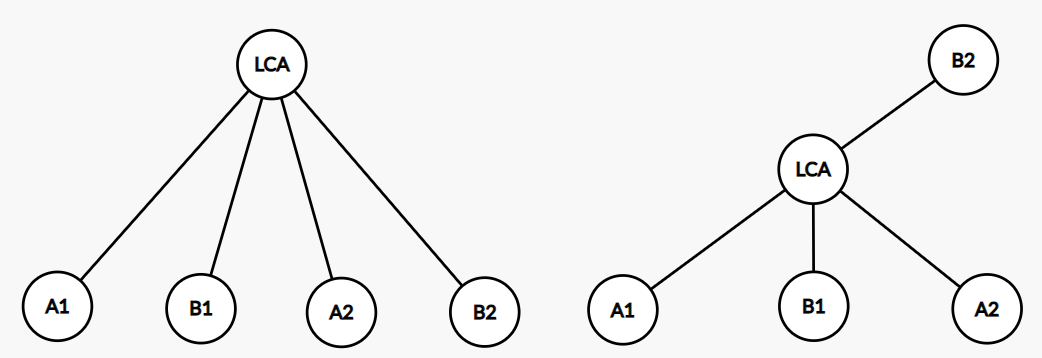
把这两种情况统一起来很麻烦，还不如分开处理呢！第一种情况就是两条路径拥有共同的 ( t lca)，第二种情况就是两条路径相交于某一条路径的 ( t lca)，他们的共性是交点一定是某个 ( t lca)，要留心这一点。

考虑下第一种情况怎么做，发现唯一的限制是四个点来自不同的子树，那么自然的想到可以求出子树的根来看是否来自不同子树。对于每一条路径都定义一个三元组 ((lca,a,b))，其中 (a,b) 分别表示两个端点的树根，如果端点是 ( t lca) 那么我们重新给个编号（因为这时候要判定为不同），为了方便我们通过 ( t swap) 是的 (a<b)

现在的问题变成了求有多少对三元组满足 ( t lca) 相同且 (a_1,b_1,a_2,b_2(a_1<b_1,a_2<b_2)) 互不相同，那么我们可以先把三元组按 ( t lca) 排序，然后按 (a) 严格递减排序（每次处理若干相同的 (a)），就能保证 (a) 互不相同。然后我们开个桶 (bt)，设访问过得三元组有 (cnt) 对，那么把 (ans-bt[b]) 计入答案，算完之后把 (bt[a],bt[b]) 加 (1)，因为 (a_i) 是递减的所以 (b_i) 和以前的 (a) 可以判重。

考虑第二种情况怎么做，交点是某个 ( t lca)，并且另一个 ( t lca) 一定是它的祖先，所以可以把三元组按 ( t lca) 的深度排序，然后我们就是要找以前出现过的 (B_1)，可以把 ( t lca) 的两个端点 (B_1,B_2)（这里的含义如图）加入树状数组中，算答案的时候就看 ( t lca_i) 的子树内的端点数量即可，注意要减去 (a_i,b_i) 子树内的端点个数。

时间复杂度 (O(nlog n))

#include <cstdio>
#include <algorithm>
using namespace std;
const int M = 300005;
#define ll long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,k,tot,Ind,f[M],dep[M],fa[M][20];
int b[2*M],bit[M],l[M],r[M];ll ans;
struct edge
{
	int v,next;
}e[2*M];
struct node
{
	int x,y,a,b,lca;
	bool operator < (const node &r) const
	{
		if(dep[lca]!=dep[r.lca]) return dep[lca]<dep[r.lca];
		if(lca!=r.lca) return lca<r.lca;
		return a>r.a;
	}
}s[M];
void dfs(int u)
{
	l[u]=++Ind;
	dep[u]=dep[fa[u][0]]+1;
	for(int i=1;i<20;i++)
		fa[u][i]=fa[fa[u][i-1]][i-1];
	for(int i=f[u];i;i=e[i].next)
	{
		int v=e[i].v;
		if(v==fa[u][0]) continue;
		fa[v][0]=u;dfs(v); 
	}
	r[u]=Ind;
}
int lca(int u,int v)
{
	if(dep[u]<=dep[v]) swap(u,v);
	for(int i=19;i>=0;i--)
		if(dep[fa[u][i]]>=dep[v])
			u=fa[u][i];
	if(u==v) return u;
	for(int i=19;i>=0;i--)
		if(fa[u][i]^fa[v][i])
			u=fa[u][i],v=fa[v][i];
	return fa[u][0];
}
int jump(int u,int x)
{
	if(u==x) return ++k;
	for(int i=19;i>=0;i--)
		if(dep[fa[u][i]]>dep[x])
			u=fa[u][i];
	return u;
}
int lowbit(int x)
{
	return x&(-x);
}
void add(int x)
{
	for(int i=x;i<=n;i+=lowbit(i))
		bit[i]++;
}
int ask(int x)
{
	int res=0;
	for(int i=x;i>=1;i-=lowbit(i))
		res+=bit[i];
	return res;
}
signed main()
{
	n=k=read();
	for(int i=1;i<n;i++)
	{
		int u=read(),v=read();
		e[++tot]=edge{v,f[u]},f[u]=tot;
		e[++tot]=edge{u,f[v]},f[v]=tot;
	}
	dfs(1);
	m=read();
	for(int i=1;i<=m;i++)
	{
		s[i].x=read();s[i].y=read();
		s[i].lca=lca(s[i].x,s[i].y);
		s[i].a=jump(s[i].x,s[i].lca);
		s[i].b=jump(s[i].y,s[i].lca);
		if(s[i].a>s[i].b)
		{
			swap(s[i].x,s[i].y);
			swap(s[i].a,s[i].b);
		}
	}
	sort(s+1,s+1+m);
	for(int i=1,j=1;i<=m;i++)
	{
		j=i;
		for(;s[i].lca==s[j+1].lca;j++);
		int cnt=0;
		for(int k=i;k<=j;k++)
		{
			int k2=k;
			while(k2<j && s[k].a==s[k2+1].a) k2++;
			for(int p=k;p<=k2;p++)
				ans+=cnt-b[s[p].b];
			for(int p=k;p<=k2;p++)
				b[s[p].a]++,b[s[p].b]++;
			cnt+=k2-k+1;k=k2;
		}
		for(int k=i;k<=j;k++)
			b[s[k].a]=b[s[k].b]=0;
		for(int k=i;k<=j;k++)
		{
			ans+=ask(r[s[k].lca])-ask(l[s[k].lca]-1);
			if(s[k].a<=n) ans-=ask(r[s[k].a])-ask(l[s[k].a]-1);
			if(s[k].b<=n) ans-=ask(r[s[k].b])-ask(l[s[k].b]-1);
		}
		for(int k=i;k<=j;k++)
			add(l[s[k].x]),add(l[s[k].y]);
		i=j;
	}
	printf("%lld
",ans);
}