令牌生成
题目描述
设 (F(q)) 表示小于等于 (q) 的数中可以表示成 (2^x-2^y) 形式的正整数的个数,其中 (x,y) 都是非负整数。
考虑将所有 (F(q)=n) 的 (q) 按照二进制表示中的 (1) 个数排序,如果有 (1) 数量相等的按照原数大小排序。
在排好序的序列中选取第 (k) 个数对 (998244353) 取模的结果作为令牌,如果序列的长度小于 (k),输出 (-1) 表示获取令牌失败。给定 (n,k) 要求回答多次询问。
(1leq n,kleq 10^{18},1leq Tleq 100000)
解法
你看着这道题好像很牛皮的样子,其实就是一个大模拟。
考虑 (2^x-2^y) 的数长成什么样子,肯定是前面一堆 (1),后面接的全是 (0):
那么答案一定是夹在上面两个数之间,这两个数是可以算出来的。
然后考虑在后面的 (cnt) 个 (0) 里面填 (1),如果填入 (i) 个 (1),那么方案数是 (C(cnt,i)),可以证明只用求 (O(log k)) 次组合数就可以得到足够的数,小于 (1e3) 的组合数可以预处理,剩下的组合数暴力算不会用多少时间。
然后考虑 (1) 填的位置,可以二分 (1) 的位置 (l),那么方案数是 (C(l,...)),这个部分也是 (O(log^2 k)) 的吧。
串
题目描述
给定 (n) 个串,有 (q) 次询问,每次询问两个串的最长公共子串。
(1leq nleq 50000),(1leq qleq 100000),串的总长小于 (50000)
解法
首先求两个串的最长公共子串是 (O(min(len_x,len_y))) 的,把小的子串丢进大的里面匹配就可以了。
然后我用到了三元环计数的思想,把长度大于 (sqrt n) 的串称为大串,否则称为小串,分别来算贡献:
- 对于小串,至多 (q) 次询问,那么时间复杂度 (O(qsqrt n))
- 对于大串,它产生贡献的时候当且仅当遇到了大串,至多产生 (O(sqrt n)),那么它的复杂度是 (O(sqrt ncdot m_i)),又因为 (sum m_ileq n),时间复杂度 (O(nsqrt n))
写的时候注意要记忆化时间复杂度才是真的。
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 100005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,ans[M];vector<int> s[M];char st[M];
struct ask
{
int x,id;
ask(int X=0,int I=0) : x(X) , id(I) {}
bool operator < (const ask &R) const
{
return x<R.x;
}
};vector<ask> q[M];
struct node
{
int fa,len,ch[26];
};
struct Sam
{
int cnt,last;node a[2*M];
void init()
{
for(int i=1;i<=cnt;i++)
{
a[i].fa=a[i].len=0;
for(int j=0;j<26;j++)
a[i].ch[j]=0;
}
cnt=last=1;
}
void add(int c)
{
int p=last,np=last=++cnt;
a[np].len=a[p].len+1;
for(;p && !a[p].ch[c];p=a[p].fa) a[p].ch[c]=np;
if(!p) a[np].fa=1;
else
{
int q=a[p].ch[c];
if(a[p].len+1==a[q].len) a[np].fa=q;
else
{
int nq=++cnt;a[nq]=a[q];
a[nq].len=a[p].len+1;
a[q].fa=a[np].fa=nq;
for(;p && a[p].ch[c]==q;p=a[p].fa) a[p].ch[c]=nq;
}
}
}
int work(int t)
{
int ans=0,p=1,len=0;
for(int i=0;i<s[t].size();i++)
{
int c=s[t][i];
while(a[p].fa && !a[p].ch[c])
{
p=a[p].fa;
len=a[p].len;
}
if(a[p].ch[c])
{
p=a[p].ch[c];
len++;
}
ans=max(ans,len);
}
return ans;
}
}A;
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
{
scanf("%s",st);
int len=strlen(st);
for(int j=0;j<len;j++)
s[i].push_back(st[j]-'a');
}
for(int i=1;i<=m;i++)
{
int x=read()+1,y=read()+1;
if(s[x].size()>s[y].size()) swap(x,y);
q[y].push_back(ask(x,i));
}
for(int i=1;i<=n;i++)
{
A.init();
for(int j=0;j<s[i].size();j++)
A.add(s[i][j]);
sort(q[i].begin(),q[i].end());
for(int j=0;j<q[i].size();j++)
{
int x=q[i][j].x,id=q[i][j].id;
ans[id]=A.work(x);
while(j<q[i].size()-1 && q[i][j+1].x==x)
{
ans[q[i][j+1].id]=ans[id];
j++;
}
}
}
for(int i=1;i<=m;i++)
printf("%d
",ans[i]);
}
随机游走
题目描述
有 (n) 个点,在点 (i) 上走一步的到的点是 (f_i),每一轮有 (p_j) 的概率走 (jin[0,m)) 步,一开始在每个点的概率都是一样的,求最后到达所有点的概率分别是多少,答案模 (998244353)
(1leq nleq60000,1leq mleq 100000,kleq1000)
部分分:(f) 是一个排列
解法
不难想到一个暴力 (dp),设 (dp[i][j]) 为第 (j) 轮在位置 (i) 的方案数,(g(i,j)) 表示 (i) 走 (j) 步到的位置,那么有转移:
这个 (dp) 难以优化,先讲一下部分分怎么做吧(虽然和正解没有关系),我们把 (f) 看成边连起来,因为它是排列所以最后得到了若干个置换环,环内每个点是等价的,那么无论怎么走最后得到的概率都是初始的概率,输出 (n) 的逆元就可以了。
正解是生成函数,首先我们要把问题转化为环套树的图,一个点走多次之后会在环里面一直转,设 (p(x)) 是走 (x) 步概率的生成函数,求出一开始给定 (p(x)) 的 (k) 次幂即可。
但是这样项数会很多,注意到会有循环,所以对于长度为 (s) 这一类 的环,设最大环套数的大小是 (n),那我们留足 (n) 项就可以了,这一类环套树的 (p(x)) 就可以一起处理,把环套树按大小排序就很容易算他们的生成函数了。根据简单的数学知识可知环套树的种类不超过 (sqrt n),此部分时间复杂度 (O(msqrt n+nlog nlog k))
对于一个环套树,我们随便选一个环上的点作为根,它连出去的那条边叫非树边。我们先断开这条边建出一棵树,然后分别统计经过非树边和不经过非树边的贡献,图画出来是这个样子,我们顺便给每个点标上深度(正负都没关系):
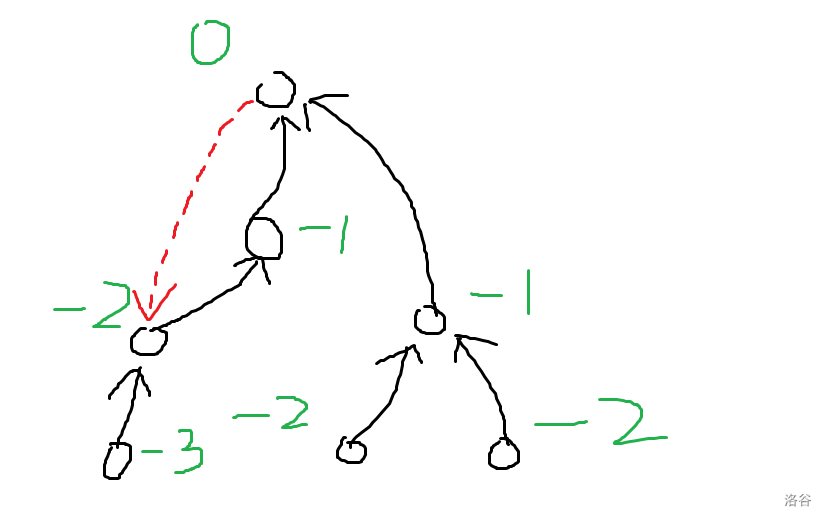
对于 不经过非树边的贡献 ,一个点仅可能由其子树中的点走到,而子树中点的 ( t dfs) 序又是一段连续的区间,我们把原图按照 ( t dfs) 序分块,我们预处理出整块和 (p(x)) 的卷积,零散块可以暴力算,时间复杂度 (O(nsqrt{nlog n}))。
对于 经过非树边的贡献 ,设 (H(x)=sum_{i=0}^nh_ix^{n-i}),其中 (h_i) 表示深度为 (-i) 的结点有多少个乘上初始概率,那么我们把 (h_i) 和 (p_i) 求卷积就可以得到最终到环上某点的概率。因为有一些非环上的点也可能混在求出的概率里面,所以减去他们的概率即可。
毒瘤题太难写了,所以没有代码。