POJ #1230 Pass-Muraille 贪心

Description

---

In modern day magic shows, passing through walls is very popular in which a magician performer passes through several walls in a predesigned stage show. The wall-passer (Pass-Muraille) has a limited wall-passing energy to pass through at most k walls in each wall-passing show. The walls are placed on a grid-like area. An example is shown in Figure 1, where the land is viewed from above. All the walls have unit widths, but different lengths. You may assume that no grid cell belongs to two or more walls. A spectator chooses a column of the grid. Our wall-passer starts from the upper side of the grid and walks along the entire column, passing through every wall in his way to get to the lower side of the grid. If he faces more than k walls when he tries to walk along a column, he would fail presenting a good show. For example, in the wall configuration shown in Figure 1, a wall-passer with k = 3 can pass from the upper side to the lower side choosing any column except column 6. 

Given a wall-passer with a given energy and a show stage, we want to remove the minimum number of walls from the stage so that our performer can pass through all the walls at any column chosen by spectators. 

Input

The first line of the input file contains a single integer t (1 <= t <= 10), the number of test cases, followed by the input data for each test case. The first line of each test case contains two integers n (1 <= n <= 100), the number of walls, and k (0 <= k <= 100), the maximum number of walls that the wall-passer can pass through, respectively. After the first line, there are n lines each containing two (x, y) pairs representing coordinates of the two endpoints of a wall. Coordinates are non-negative integers less than or equal to 100. The upper-left of the grid is assumed to have coordinates (0, 0). The second sample test case below corresponds to the land given in Figure 1. 

Output

There should be one line per test case containing an integer number which is the minimum number of walls to be removed such that the wall-passer can pass through walls starting from any column on the upper side. 

Sample Input

2
3 1
2 0 4 0
0 1 1 1
1 2 2 2
7 3
0 0 3 0
6 1 8 1
2 3 6 3
4 4 6 4
0 5 1 5
5 6 7 6
1 7 3 7

Sample Output

1
1

Hint

Walls are parallel to X.

　　更多的测试样例在这：链接

　　还有些特殊的测试样例需要测试，可以在题目下的 DISCUSS 里翻一翻。

思路

---

　　问题概述如下：

　　　　

　　

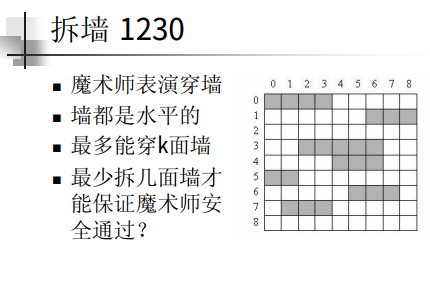
　　我们需要考虑，如何拆墙才是最优的。是拆最长的墙的吗？并不是的，因为最长的墙可能对之后要走的列没有帮助。如何让拆掉的墙对之后的列帮助最大呢？最优的办法就是让拆掉右端尽可能长的墙，那么当魔术师走之后的列的时候需要翻的墙就会更少。

　　　　

　　　　

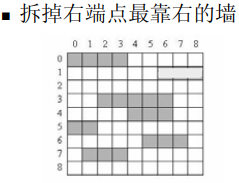
　　WA了N次终于过了。优化了一下逻辑，其实每列需要删除的墙数可以先通过遍历该列而计算出来。知道该列要删除多少堵墙后再去利用贪心删墙会更方便。

　　

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
#define INT_MIN -9999
const int MAX_X = 100, MAX_Y = 100;
bool map[MAX_X + 5][MAX_Y + 5]; //网格，true 有墙, false 无墙
int n, k; //总墙数与魔术师能翻过的墙数

struct Point {
    int x;
    int y;
};

struct Wall {
    Point start;
    Point end;
    bool remove_flag;
};

vector<Wall> w; //存储所有墙的信息

int greedy_remove (const int& max_x, const int& max_y, vector<Wall>& w) {
    int remove_counter = 0;
    for (int i = 0; i <= max_x; i++) {
        int barriers = 0;
        for (int j = 0; j <= max_y; j++) 
            if (map[i][j]) barriers++;
        //贪心删墙
        while (barriers > k) {
            int dist = INT_MIN; //阻碍前进的墙的右端到当前列的距离
            int num = INT_MIN; //需要删除的墙的序号
            //贪心选择当前列到墙右端最远的墙
            for (int m = 1; m <= n; m++) {
                if (!w[m].remove_flag && w[m].end.x >= i && w[m].start.x <= i) {
                    int dist2 = w[m].end.x - i;
                    if (dist < dist2) {
                        num = m;
                        dist = dist2;
                    }
                }
            }
            //删墙
            if (num != INT_MIN) {
                for (int i2 = w[num].start.x; i2 <= w[num].end.x; i2++) {
                    map[i2][w[num].start.y] = false;
                }
                w[num].remove_flag = true;
                barriers--;
                remove_counter++;    
            }    
        } //while(barriers > k)
    } //i <= max_x
    return remove_counter;
} //int greedy_remove()

int main(void) {
    int t;
    cin >> t;
    while (t--) {
        cin >> n >> k;
        //建墙
        memset(map, false, sizeof(map));
        w.clear();
        w.resize(n+1);
        int max_x = 0, max_y = 0; //记录最大行与最大列
        for (int i = 1; i <= n; i++) {
            int x1, y1, x2, y2;
            cin >> x1 >> y1 >> x2 >> y2;
            //可能先输入墙的右端点
            if (x1 > x2) 
                std::swap(x1,x2);
            for (int j = x1; j <= x2; j++)
                map[j][y1] = true;
            w[i].start.x = x1;
            w[i].start.y = y1;
            w[i].end.x = x2;
            w[i].end.y = y2;
            w[i].remove_flag = false;
            if (max_x < x2)
                max_x = x2;
            if (max_y < y2)
                max_y = y2;
        }
        //贪心删墙
        int ans = greedy_remove(max_x, max_y, w);
        cout << ans << endl;
    } //while (t--)

    vector<Wall>().swap(w);
    return 0;
} //int main()