Matlab神经网络工具箱中提供了两个自带的数据标准化处理的函数——mapstd和mapminmax,本文试图解析一下这两个函数的用法。
一、mapstd
mapstd对应我们数学建模中常使用的Z-Score标准化方法。
What is Z-Score?(摘自Orange_Spotty_Cat的CSDN博客,原文链接https://blog.csdn.net/Orange_Spotty_Cat/article/details/80312154)
简介
Z-Score标准化是数据处理的一种常用方法。通过它能够将不同量级的数据转化为统一量度的Z-Score分值进行比较。一句话解释版本:
Z-Score通过(x-μ)/σ将两组或多组数据转化为无单位的Z-Score分值,使得数据标准统一化,提高了数据可比性,削弱了数据解释性。
Z-Score标准化是数据处理的方法之一。在数据标准化中,常见的方法有如下三种:
- Z-Score 标准化
- 最大最小标准化
- 小数定标法
Z-Score的定义
Z-Score处理方法处于整个框架中的数据准备阶段。也就是说,在源数据通过网络爬虫、接口或其他方式进入数据库中后,下一步就要进行的数据预处理阶段中的重要步骤。数据分析与挖掘中,很多方法需要样本符合一定的标准,如果需要分析的诸多自变量不是同一个量级,就会给分析工作造成困难,甚至影响后期建模的精准度。
举例来说,假设我们要比较A与B的考试成绩,A的考卷满分是100分(及格60分),B的考卷满分是700分(及格420分)。很显然,A考出的70分与B考出的70分代表着完全不同的意义。但是从数值来讲,A与B在数据表中都是用数字70代表各自的成绩。
那么如何能够用一个同等的标准来比较A与B的成绩呢?Z-Score就可以解决这一问题。
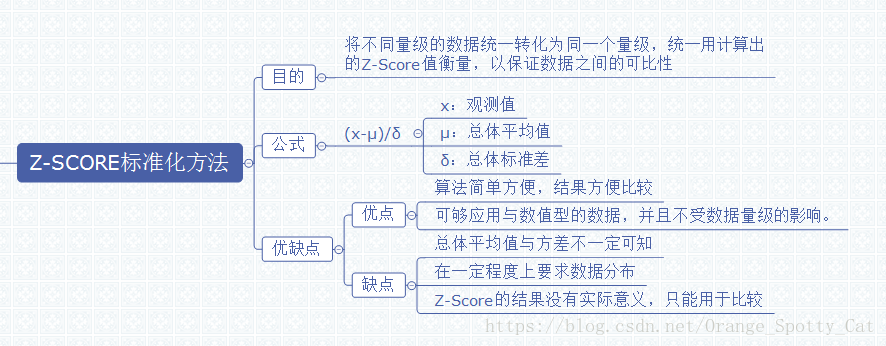
下图描述了Z-Score的定义以及各种特征。
Z-Score的目的
如上图所示,Z-Score的主要目的就是将不同量级的数据统一转化为同一个量级,统一用计算出的Z-Score值衡量,以保证数据之间的可比性。
Z-Score的理解与计算
在对数据进行Z-Score标准化之前,我们需要得到如下信息:1)总体数据的均值(μ)
在上面的例子中,总体可以是整个班级的平均分,也可以是全市、全国的平均分。
2)总体数据的标准差(σ)
这个总体要与1)中的总体在同一个量级。
3)个体的观测值(x)
在上面的例子中,即A与B各自的成绩。
通过将以上三个值代入Z-Score的公式,即:
我们就能够将不同的数据转换到相同的量级上,实现标准化。
重新回到前面的例子,假设:A班级的平均分是80,标准差是10,A考了90分;B班的平均分是400,标准差是100,B考了600分。
通过上面的公式,我们可以计算得出,A的Z-Score是1((90-80)/10),B的Z-Socre是2((600-400)/100)。因此B的成绩更为优异。
反之,若A考了60分,B考了300分,A的Z-Score是-2,B的Z-Score是-1。因此A的成绩更差。
因此,可以看出来,通过Z-Score可以有效的把数据转换为统一的标准,但是需要注意,并进行比较。Z-Score本身没有实际意义,它的现实意义需要在比较中得以实现,这也是Z-Score的缺点之一。
Z-Score的优缺点
Z-Score最大的优点就是简单,容易计算,在R中,不需要加载包,仅仅凭借最简单的数学公式就能够计算出Z-Score并进行比较。此外,Z-Score能够应用于数值型的数据,并且不受数据量级的影响,因为它本身的作用就是消除量级给分析带来的不便。但是Z-Score应用也有风险。首先,估算Z-Score需要总体的平均值与方差,但是这一值在真实的分析与挖掘中很难得到,大多数情况下是用样本的均值与标准差替代。其次,Z-Score对于数据的分布有一定的要求,正态分布是最有利于Z-Score计算的。最后,Z-Score消除了数据具有的实际意义,A的Z-Score与B的Z-Score与他们各自的分数不再有关系,因此Z-Score的结果只能用于比较数据间的结果,数据的真实意义还需要还原原值。
---------------------
作者:Orange_Spotty_Cat
来源:CSDN
原文:https://blog.csdn.net/Orange_Spotty_Cat/article/details/80312154
版权声明:本文为博主原创文章,转载请附上博文链接!
了解了Z-Score标准化是什么之后,我们来看一下matlab中该标准化对应的函数的help:
mapstd Map matrix row means and deviations to standard values.
mapstd processes input and target data by mapping its mean and standard deviations to 0 and 1 respectively.
[Y,settings] = mapstd(X) takes a matrix and returns it transformed with the settings used to perform the transform.
Here data with non-standard mean/deviations in each row is transformed.
x1 = [log(rand(1,20)*5-1); rand(1,20)*20-10; rand(1,20)-1]; [y1,settings] = mapstd(x1)
mapstd('apply',X,settings) transforms X consistent with settings returned by a previous transformation.
x2 = [log(rand(1,20)*5-1); rand(1,20)*20-10; rand(1,20)-1]; y2 = mapstd('apply',x2,settings)
mapstd('reverse',Y,settings) reverse transforms Y consistent with settings returned by a previous transformation.
x1_again = mapstd('reverse',y1,settings)
可以看到,mapstd的使用方法有如下几种:
[Y, PS] = mapstd(X)
[Y, PS] = mapstd(X, fp)
[Y, PS] = mapstd(X, ymeans, ystd)
Y = mapstd('apply', X, PS)
X = mapstd('reverse', Y, PS)
dx_dy = mapstd('dx_dy', X, Y, PS)
我们依次来看一下这五种使用方法:
①最常规的、一般来说最先调用的使用方法:[Y, settings] = mapstd(X)
调用形式:X是待处理的数据,数据格式如下表所示(每一列代表一个对象的m个属性,每一行是所有对象的一条属性)
| x1 | x1 | x1 | x1 | x1 | ... |
| x2 | x2 | x2 | x2 | x2 | ... |
| x3 | x3 | x3 | x3 | x3 | ... |
|
... |
... | ... | ... | ... | ... |
| xm | xm | xm | xm | xm | ... |
假如我们的原始数据如下(节选自《数学建模算法与应用》第二版,P209页表9.1):(有黑色边框的部分是实际的数据表)
| 省(自治区、直辖市)名 | x1 | x2 | x3 | x4 | x5 |
| 山西 | 8.35 | 23.53 | 7.51 | 8.62 | 17.42 |
| 内蒙古 | 9.25 | 23.75 | 6.61 | 9.19 | 17.77 |
| 吉林 | 8.19 | 30.50 | 4.72 | 9.78 | 16.28 |
则使用mapstd函数对该数据表进行Z-Score标准化的代码应为:
clc,clear;
origin=[8.35 23.53 7.51 8.62 17.42; 9.25 23.75 6.61 9.19 17.77; 8.19 30.50 4.72 9.78 16.28]; [y, ps] = mapstd(origin') %注意数据表和mapstd函数所要求的格式不同,因此需要先对其进行一次转置 whos ps.xmean ps.xstd
该段代码运行结果如下:
y = -0.4317 1.1433 -0.7117 -0.6049 -0.5494 1.1543 0.8638 0.2317 -1.0955 -0.9942 -0.0115 1.0057 0.3380 0.7872 -1.1252 ps = xrows: 5 yrows: 5 xmean: [5x1 double] xstd: [5x1 double] ymean: 0 ystd: 1 no_change: 0 gain: [5x1 double] xoffset: [5x1 double] Name Size Bytes Class Attributes origin 3x5 120 double ps 1x1 1777 struct y 5x3 120 double ans = 8.5967 25.9267 6.2800 9.1967 17.1567 ans = 0.5714 3.9622 1.4240 0.5800 0.7791
可以看到,该调用格式的第一返回值是Z-Score标准化后的数据矩阵(格式与传入的矩阵的格式相同),第二返回值是一个有着行数、列数、平均值、标准差等数据的结构体,其中xmean的第一行(第一个元素)记录的是所有数据的第一项指标的均值,第二行(第二个元素)记录的是所有数据的第二项指标的均值;xstd则是这些指标的标准差,与xmean类同。
另外的,该调用格式的第二返回值包含了ymean,ystd等信息,因此可以用作[Y, PS] = mapstd(X, fp)的第二参数;第二返回值同时包含了xmean, xstd等信息,因此也可以用作Y = mapstd('apply', X, PS)、X = mapstd('reverse', Y, PS)、dx_dy = mapstd('dx_dy', X, Y, PS)三个调用方式的PS参数
②传入ymean和ystd的使用方法:[Y, PS] = mapstd(X, ymeans, ystd)和[Y, PS] = mapstd(X, fp)
默认情况下,ymeans=0,ystd=1(在ymeans=0和ystd=1的情况下,该调用方法就等同于①中所讲的使用方法)
除了将ymeans和ystd作为两个参数传给函数以外,还可以将这两个参数放入一个结构体,再将该结构体传给函数
示例代码如下:(该段代码来自老子今晚不加班的CSDN博客,原文链接:https://blog.csdn.net/hqh45/article/details/42965481)
x=[2,3,4,5,6;7,8,9,10,11]; y=[2,3;4,5]; [xx,ps]=mapstd(x,0,1) fp.ymean=0; fp.ystd=1; [xx,ps]=mapstd(x,fp)
③传入训练数据标准化时得到的ps,来计算预测数据的标准化,对应的调用格式为Y = mapstd('apply', X, PS)
该调用格式实际上是根据已有给定的数据标准化处理映射PS,将给定的数据X标准化成Y
示例代码如下:
注:假设我们的待预测数据如下:(节选自《数学建模算法与应用》第二版,P209页表9.1):(有黑色边框的部分是实际的数据表)
| 省(自治区、直辖市)名 | x1 | x2 | x3 | x4 | x5 |
| 西藏 | 7.94 | 39.65 | 20.97 | 20.82 | 22.52 |
| 上海 | 8.28 | 64.34 | 8.00 | 22.22 | 20.06 |
| 广东 | 12.47 | 76.39 | 5.52 | 11.24 | 14.52 |
clc,clear; origin=[8.35 23.53 7.51 8.62 17.42; 9.25 23.75 6.61 9.19 17.77; 8.19 30.50 4.72 9.78 16.28]; yuce=[7.94 39.65 20.97 20.82 22.52; 8.28 64.34 8.00 22.22 20.06; 12.47 76.39 5.52 11.24 14.52]; [y, ps] = mapstd(origin'); %注意数据表和mapstd函数所要求的格式不同,因此需要先对其进行一次转置 dd=mapstd('apply',yuce',ps) %注意这里需要转置
④根据已有给定的数据标准化处理映射PS,将给定的标准化数据Y反标准化,对应的调用格式为X = mapstd('reverse', Y, PS)
与③类同,只不过求解方向从X->Y变成了从Y->X
示例代码如下:
clc,clear; origin=[8.35 23.53 7.51 8.62 17.42; 9.25 23.75 6.61 9.19 17.77; 8.19 30.50 4.72 9.78 16.28]; yuce=[7.94 39.65 20.97 20.82 22.52; 8.28 64.34 8.00 22.22 20.06; 12.47 76.39 5.52 11.24 14.52]; [y, ps] = mapstd(origin'); %注意数据表和mapstd函数所要求的格式不同,因此需要先对其进行一次转置 dd=mapstd('apply',yuce',ps) %注意这里需要转置 dddd=mapstd('reverse',dd,ps)
运行结果如下:
dd = -1.1492 -0.5542 6.7783 3.4636 9.6951 12.7364 10.3162 1.2079 -0.5337 20.0392 22.4529 3.5228 6.8838 3.7264 -3.3841 dddd = 7.9400 8.2800 12.4700 39.6500 64.3400 76.3900 20.9700 8.0000 5.5200 20.8200 22.2200 11.2400 22.5200 20.0600 14.5200
可以看到,我们对标准化后的数据再用同样的映射ps进行一次逆标准化后,就可以得到原始数据(当然,该例子中得到的结果是原始数据表格的转置)
⑤调用格式dx_dy = mapstd('dx_dy', X, Y, PS)
该调用格式不是很常用,matlab的help中未给出该调用格式的相关说明,这里采用天涯de何处的新浪博客给出的说法:根据给定的矩阵X、标准化矩阵Y及映射PS,获取逆向导数(reverse derivative)。如果给定的X和Y是m行n列的矩阵,那么其结果dx_dy是一个1×n结构体数组,其每个元素又是一个m×n的对角矩阵。(原文链接地址:http://blog.sina.com.cn/s/blog_b3509cfd0101bt9u.html)
二、mapminmax
mapminmax函数对应的是我们另外一个常用的标准化方式——最大最小归一化,其功能主要是将原始数据线性化的方法转换到[0,1]的范围,归一化公式如下:

其中xmax为样本数据的最大值,xmin为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时,可能导致xmax和xmin的变化,需要重新定义。
mapminmax的matlab使用方式与mapstd类似,这里不再赘述,也可参考天涯de何处的新浪博客:
一、mapminmax
mapminmax按行逐行地对数据进行标准化处理,将每一行数据分别标准化到区间[ymin, ymax]内,其计算公式是:y = (ymax-ymin)*(x-xmin)/(xmax-xmin) + ymin。如果某行的数据全部相同,此时xmax=xmin,除数为0,则Matlab内部将此变换变为y = ymin。
(1) [Y,PS] = mapminmax(X,YMIN,YMAX)——将数据X归一化到区间[YMIN,YMAX]内,YMIN和YMAX为调用mapminmax函数时设置的参数,如果不设置这两个参数,这默认归一化到区间[-1, 1]内。标准化处理后的数据为Y,PS为记录标准化映射的结构体。
【例1】Matlab命令窗口输入:X=12+8*randn(6,8); [Y,PS] = mapminmax(X,0,1),则将随机数矩阵X按行逐行标准化到区间[0,1]内,并返回标准矩阵Y和结构体PS(至于它的作用,将在后面介绍到),它记录了X的行数、X中各行的最大值与最小值等信息。这里:
PS =
name: 'mapminmax'
xrows: 6
xmax: [6x1 double]
xmin: [6x1 double]
xrange: [6x1 double]
yrows: 6
ymax: 1
ymin: 0
yrange: 1
no_change: 0
gain: [6x1 double]
xoffset: [6x1 double]
(2) [Y,PS] = mapminmax(X,FP)——将YMIN和YMAX组成的结构体FP作为映射参数(FP.ymin和FP.ymax.)对进行标准化处理。
【例2】Matlab命令窗口输入:XX=12+8*randn(6,8); FP.ymin=-2; FP.ymax=2; [YY,PSS] = mapminmax(XX,FP),则将随机数矩阵X按行逐行标准化到区间[-2,2]内,并返回标准矩阵YY和结构体PSS。
(3) Y = mapminmax('apply',X,PS)——根据已有给定的数据标准化处理映射PS,将给定的数据X标准化为Y。
【例3】在例1的基础上,Matlab命令窗口输入:XXX=23+11*randn(6,8); YYY= mapminmax('apply',XXX,PS),则根据例1的标准化映射,将XXX标准化(结果可能不全在先前设置的[YMIN,YMAX]内,这取决于XXX中数据相对于X中数据的最大值与最小值的比较情况)。注意:此时,XXX的行数必须与X的行数(PS中已记录)相等,否则无法进行;列数可不等。
(4) X = mapminmax('reverse',Y,PS)——根据已有给定的数据标准化处理映射PS,将给定的标准化数据Y反标准化。
【例4】在例1的基础上,Matlab命令窗口输入:YYYY=rand(6,8); XXXX = mapminmax('reverse', YYYY,PS),则根据例1的标准化映射,将YYYY反标准化。注意:此时,YYYY的行数必须与X的行数(PS中已记录)相等,否则无法进行;列数可不等。
(5) dx_dy = mapminmax('dx_dy',X,Y,PS) ——根据给定的矩阵X、标准化矩阵Y及映射PS,获取逆向导数(reverse derivative)。如果给定的X和Y是m行n列的矩阵,那么其结果dx_dy是一个1×n结构体数组,其每个元素又是一个m×n的对角矩阵。这种用法不常用,这里不再举例。
三、Z-Score标准化和最大最小归一化
参照云时之间的腾讯云文章:(原文链接:https://cloud.tencent.com/developer/article/1091627)
归一化的依据非常简单,不同变量往往量纲不同,归一化可以消除量纲对最终结果的影响,使不同变量具有可比性。比如两个人体重差10KG,身高差0.02M,在衡量两个人的差别时体重的差距会把身高的差距完全掩盖,归一化之后就不会有这样的问题。
标准化的原理比较复杂,它表示的是原始值与均值之间差多少个标准差,是一个相对值,所以也有去除量纲的功效。同时,它还带来两个附加的好处:均值为0,标准差为1。
均值为0有什么好处呢?它可以使数据以0为中心左右分布(这不是废话嘛),而数据以0为中心左右分布会带来很多便利。比如在去中心化的数据上做SVD分解等价于在原始数据上做PCA;机器学习中很多函数如Sigmoid、Tanh、Softmax等都以0为中心左右分布(不一定对称)。
标准差为1有什么好处呢?这个更复杂一些。对于xixi与xi′xi′两点间距离,往往表示为
其中dj(xij,xi′j)dj(xij,xi′j)是属性jj两个点之间的距离,wjwj是该属性间距离在总距离中的权重,注意设wj=1,∀jwj=1,∀j并不能实现每个属性对最后的结果贡献度相同。对于给定的数据集,所有点对间距离的平均值是个定值,即
是个常数,其中
可见第jj个变量对最终整体平均距离的影响是wj⋅¯djwj⋅d¯j,所以设wj∼1/¯djwj∼1/d¯j可以使所有属性对全数据集平均距离的贡献相同。现在设djdj为欧式距离(或称为二范数)的平方,它是最常用的距离衡量方法之一,则有
其中varjvarj是Var(Xj)Var(Xj)的样本估计,也就是说每个变量的重要程度正比于这个变量在这个数据集上的方差。如果我们让每一维变量的标准差都为1(即方差都为1),每维变量在计算距离的时候重要程度相同。
在涉及到计算点与点之间的距离时,使用归一化或标准化都会对最后的结果有所提升,甚至会有质的区别。那在归一化与标准化之间应该如何选择呢?根据上一节我们看到,如果把所有维度的变量一视同仁,在最后计算距离中发挥相同的作用应该选择标准化,如果想保留原始数据中由标准差所反映的潜在权重关系应该选择归一化。另外,标准化更适合现代嘈杂大数据场景。