
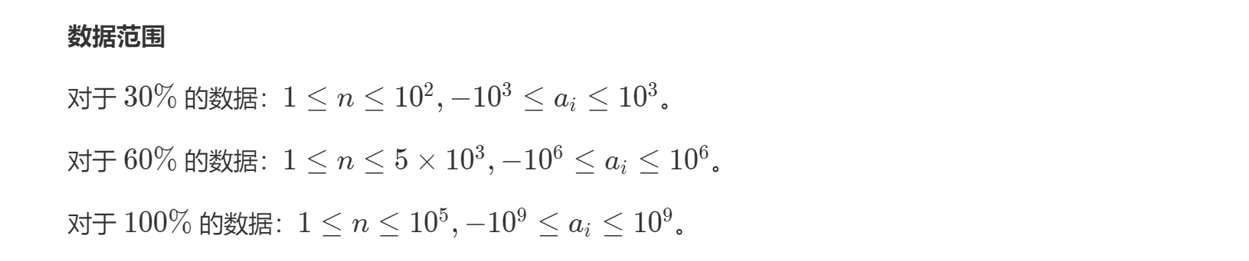
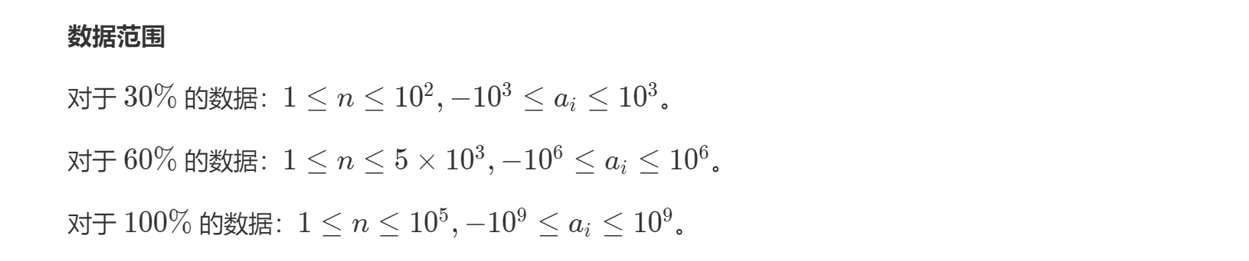
样例输入:
3
1 -2 1
样例输出:
2
方法一:
将环形数组拆分成为普通数组,(通过搬运复制数据到尾部),再求前缀和,找出最大前缀和。因为枚举了每一个起点,所以最大连续和也一定出现在前缀和中。。。
1 #include<iostream> 2 using namespace std; 3 4 int n; 5 long long arr[20010]; 6 long long s[20010]; 7 8 int main(){ 9 /*freopen("in.txt","r",stdin);*/ 10 cin>>n; 11 for(int i=1;i<=n;i++){ 12 cin>>arr[i]; 13 } 14 int ans = -1; 15 int i; 16 for(i = 1;i<=n;i++){ 17 //搬运数据 18 for(int j=1;j<i;j++){ 19 arr[n+j] = arr[j]; 20 } 21 int len = n + i; 22 //求出最大的连续和(前缀和) 23 s[i-1] = 0; 24 for(int p = i;p<=len;p++){ 25 s[p] = s[p-1] + arr[p]; 26 if(s[p] > ans) ans = s[p]; 27 } 28 29 } 30 cout<<ans<<endl; 31 return 0; 32 }
方法二:
1:如果子序列的最大和在1~n的范围内,直接输出最大值即可。2:如果子序列的最大和横跨了尾部和头部,则先求出连续的最小子序列和,然后用总和减去最小子串和就是最大子串和,所以求
1~n的最大和最小连续子序列和(记为Mx和Mi),然后输出Mx和sum-Mi即可。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int maxn = 2e5+5; 7 #define INF 0x3f3f3f3f 8 #define ll long long 9 10 ll sum,mx,mi,Mx,Mi; 11 ll num[maxn],n; 12 13 int main(){ 14 /*freopen("in.txt","r",stdin);*/ 15 cin>>n; 16 memset(num,0,sizeof(num)); 17 Mx=-INF; 18 Mi=INF; 19 mx=mi=sum=0; 20 21 for( int i=0; i<n; i++ ){ 22 cin>>num[i]; 23 sum+=num[i]; 24 mx+=num[i]; 25 mi+=num[i]; 26 Mx=max(Mx,mx); 27 Mi=min(Mi,mi); 28 if(mi>0) mi=0; 29 if(mx<0) mx=0; 30 } 31 cout<<max(Mx,sum-Mi)<<endl; 32 return 0; 33 }