堆操作（3）-堆排序

一、选择排序的弊端

需要n^2。核心的耗时在每次寻找最大值。

    public static void selectionSort(int[] list) {
        for (int index = 0; index < list.length - 1; index++) {
            int minIndex = findMinIndex(index, list);//寻找最小的index
            int temp = list[index];
            list[index] = list[minIndex];//把最小的值赋值到当前节点，完成一次排序
            list[minIndex] = temp;
        }
    }

    private static int findMinIndex(int startIndex, int[] list) {
        int minData = list[startIndex];
        int minIndex = startIndex;
        for (int i = startIndex + 1; i < list.length; i++) {
            if (minData > list[i]) {
                minData = list[i];
                minIndex = i;
            }
        }
        return minIndex;
    }

主要开销就是findMinIndex，这个方法的复杂度是O(n)。如果要进一步优化选择排序，就需要找到一个复杂度小于O(n)的findMinIndex的方法。

二、引入堆

采用堆数据结构，每次返回堆顶元素，就是最大值（从大到小排序。如果从小到大，使用小顶堆即可）。查找过程为log(n)。这样整个选择排序的整体算法时间复杂度从n^2降为nlog(n)。

但是这种算法最大的问题在于

1. 额外引入了一个数组，空间复杂度为log(n)。
2. 同时涉及到大量的数据的拷贝。

    public static void advanceSelectionSort(Integer[] list) {
        HeapStruct heapStruct = getHeapStruct(list);//创建堆
        int[] tempList = new int[list.length];//额外的空间。
        for (int index = 0; index < list.length - 1; index++) {
            Integer maxValue = HeapUtil.deleteMax(heapStruct);//寻找最大的index
            tempList[index] = maxValue;
        }
        for (int i = 0; i < list.length; i++) {
            list[i] = tempList[i];//大量的数据复制
        }
    }

三、堆排序

堆排序的引入：之前有文章介绍过如何把一个平衡二叉树调整为一个大顶堆，给定堆顶元素的index，从上往下找，一次循环结束后，index对应的元素（堆顶）便是最大值。

堆排序的核心就是利用大顶堆的调整方法，主要改进点便是，一次调整完成后把堆顶元素和数组的最后一个元素互换，同时把堆的规模缩小1。依次类推，一直到堆的规模为0即可。

3.1 演示



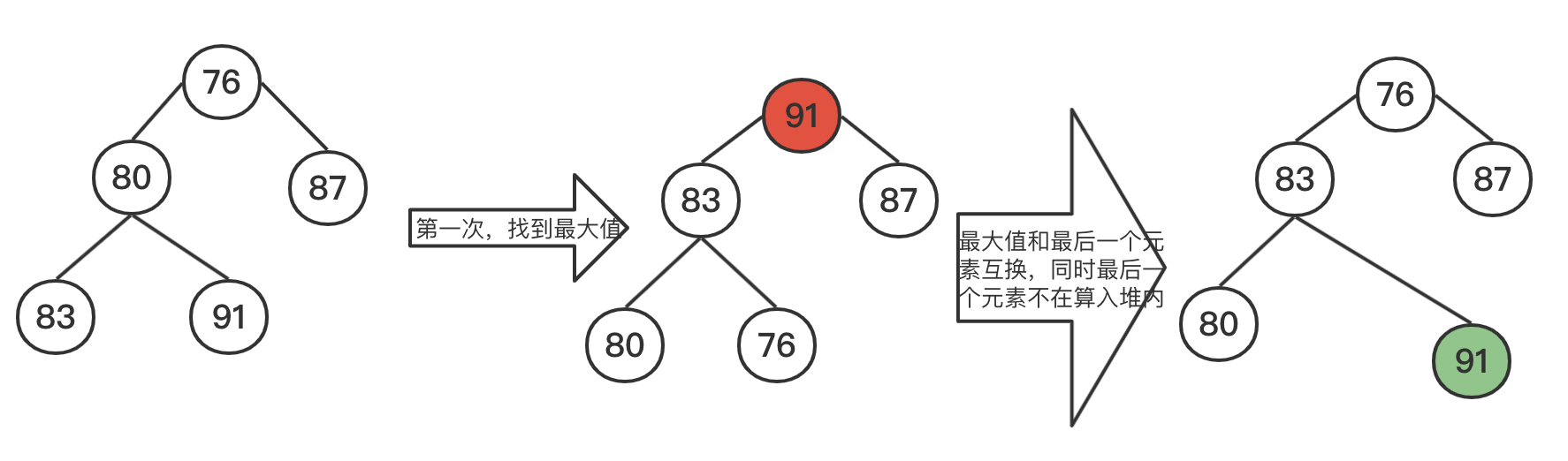
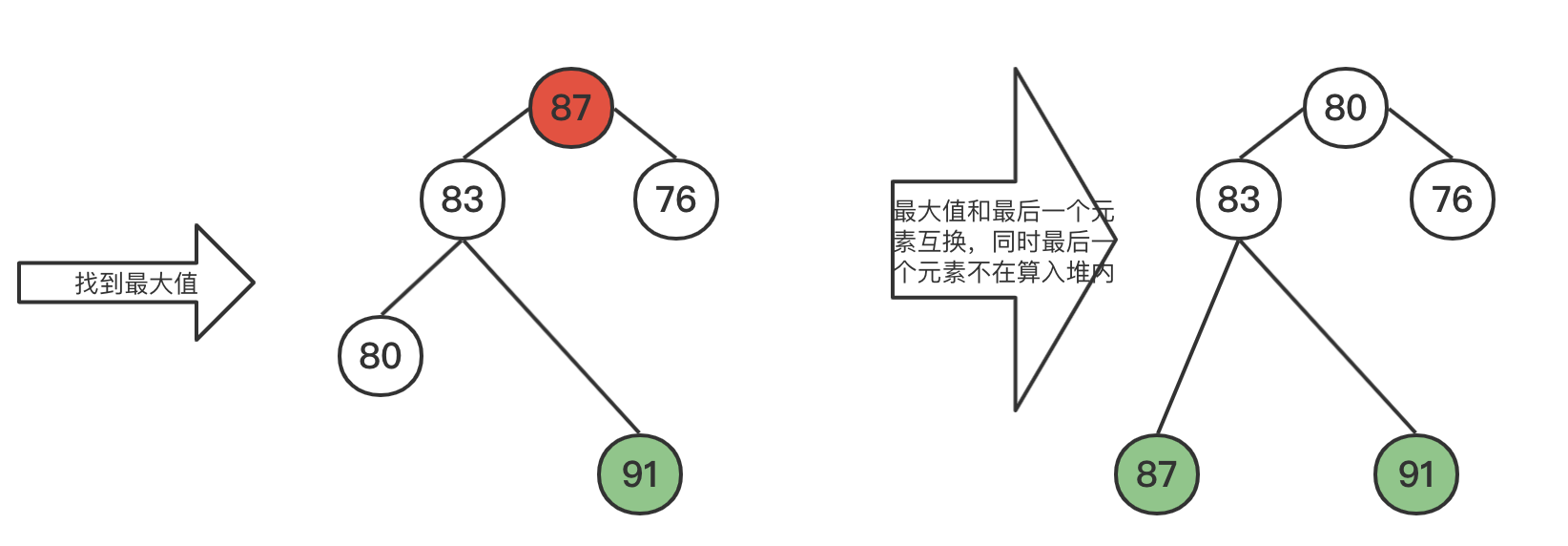
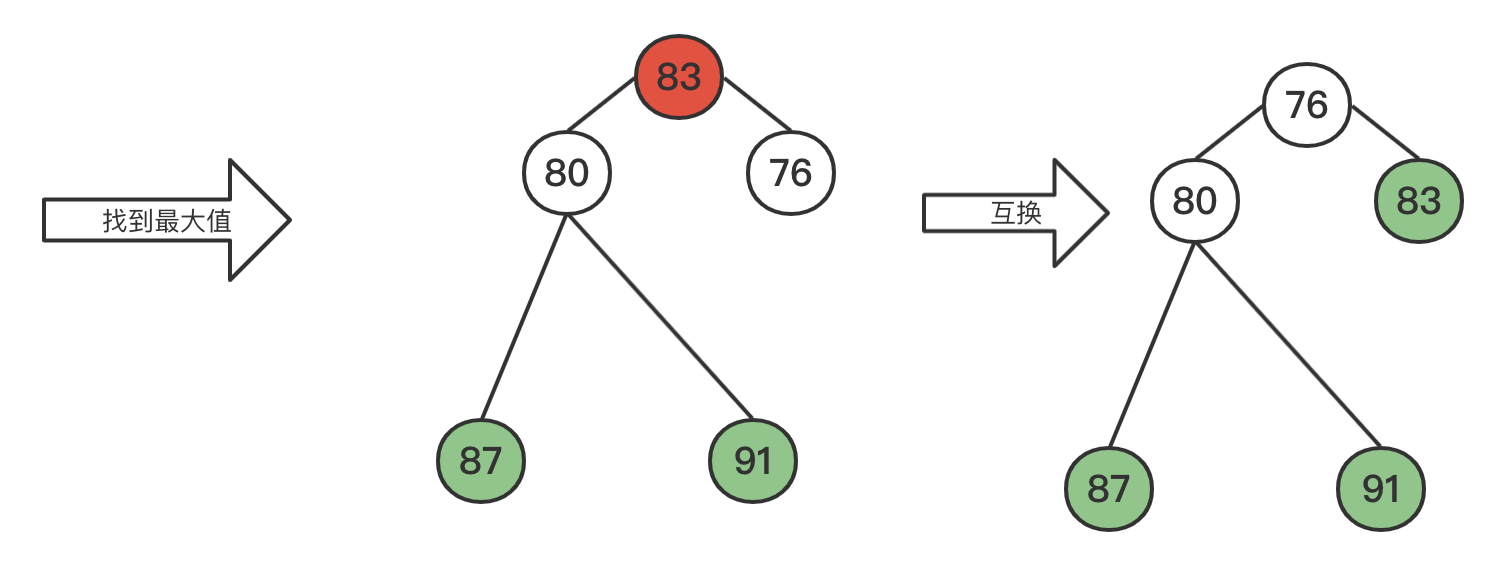
没有额外增加空间，同时利用了堆logn的时间复杂度。

3.2 代码

    public static void heapSort(Integer[] list) {
        HeapStruct heapStruct = getHeapStruct(list);//创建堆--此时，堆顶元素为最大值
        for (int index = list.length - 1; index > 0; index++) {
            Integer temp = list[0];
            list[0] = list[index];
            list[index] = temp;//把堆顶元素和最后一个元素互换
            percDown(heapStruct, 0, index);//index每次减一，堆的规模慢慢变小，每次percDown结束，堆顶元素都是最大值
        }
    }

    public static void percDown(HeapStruct heapStruct, int rootIndex, int heapSize) {
        Integer[] elements = heapStruct.getElements();
        Integer rootValue = elements[rootIndex];
        int parentIndex = rootIndex;
        while (parentIndex * 2 + 1 < heapSize) {
            int childIndex = parentIndex * 2 + 1;
            if (childIndex < heapSize - 1 && elements[childIndex].compareTo(elements[childIndex + 1]) < 0) {
                childIndex = childIndex + 1;
            }
            if (rootValue.compareTo(elements[childIndex]) > 0) {
                break;
            } else {
                elements[parentIndex] = elements[childIndex];
                parentIndex = childIndex;
            }
        }
        elements[parentIndex] = rootValue;
    }