一、最大堆建立
给定N个元素,按照最大堆的要求将元素放入数组中。
两种做法:
- 通过插入,依次将N个元素插入一个空堆中,复杂度为nlogn。
- 线性复杂度建立堆
- 先将N个元素按照顺序存入,先满足完全二叉树的特性
- 调整各个节点,让其满足最大堆的特性
本文主要介绍第二种方法,线性复杂度创建堆。
二、线性复杂度创建堆
默认创建一个完全二叉树
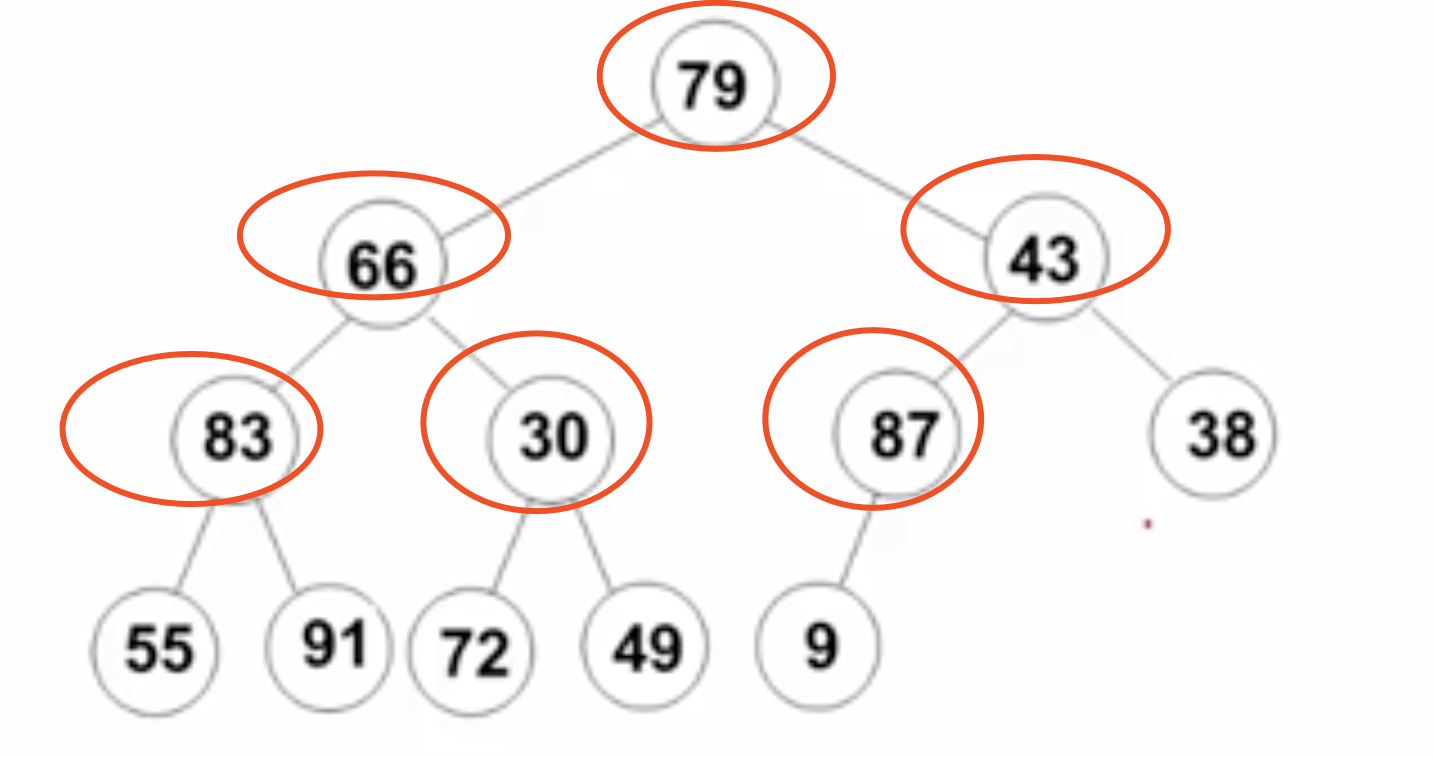
从最后一个节点的父节点【第一个父节点】(87)开始调整。87大于9。默认不变,当前子树是一个堆。
第二个父节点30。最大子节点为72。把72个30继续互换,当前子树是一个堆。
第三个父节点83。最大子节点为91。把91和83进行互换,当前子树也是一个堆。
三次交换后,树的结构如下。
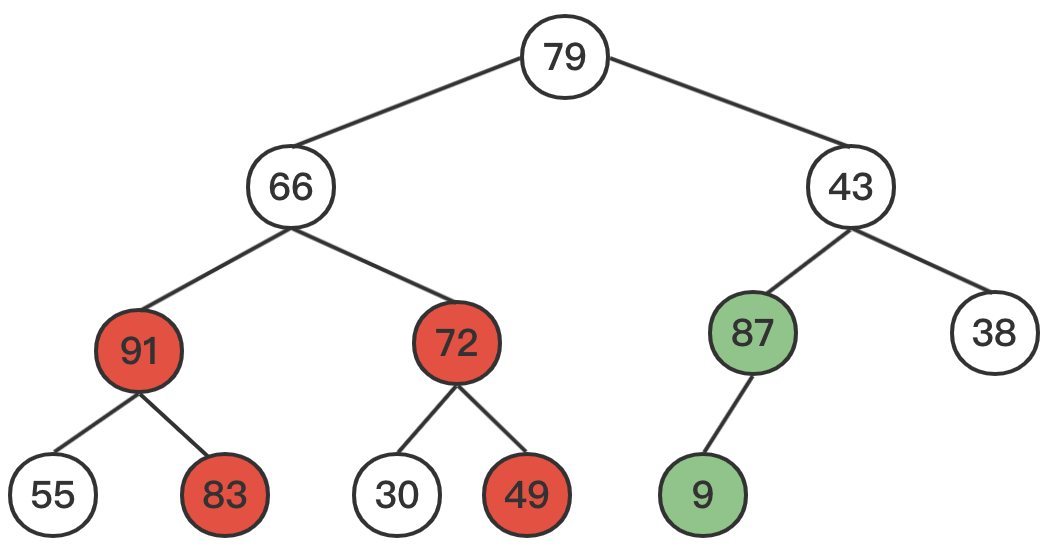
从43开始调整。87大于43,互换,当前子树是一个堆。
从66开始调整,91大于66进行互换。83大于66,再次进行互换,当前子树是一个堆。

最后调整根节点;91和79互换。83和79进行互换,至此。整颗树都变成了一个堆。
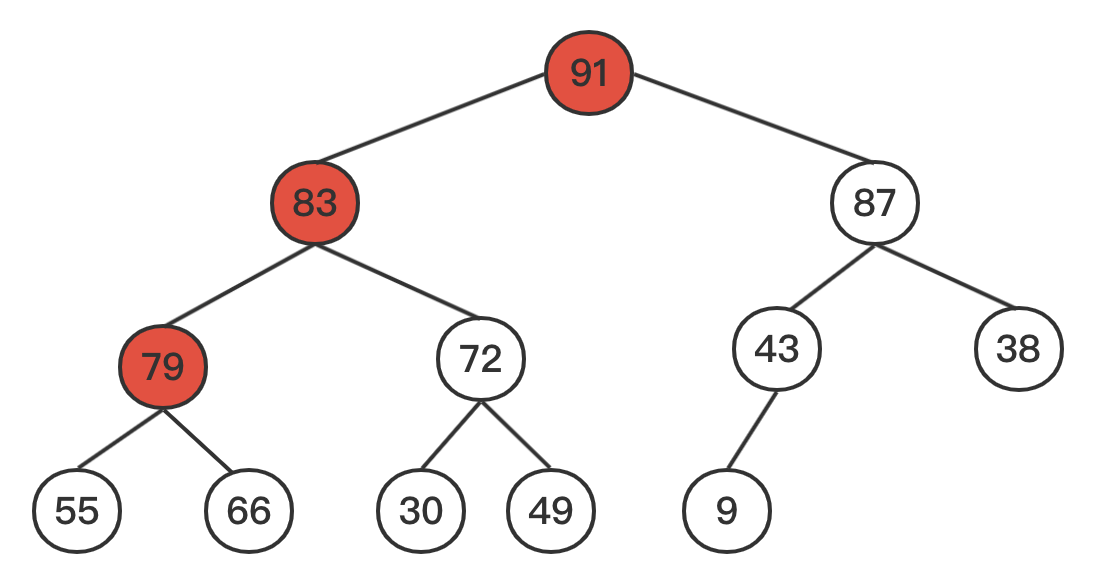
代码
public static void percDown(HeapStruct heapStruct, int rootIndex) {
Integer[] elements = heapStruct.getElements();
Integer rootValue = elements[rootIndex];
int parentIndex = rootIndex;
while (parentIndex * 2 <= heapStruct.getSize() - 2) {
int childIndex = parentIndex * 2 + 1;
if (childIndex < heapStruct.getSize() - 1 && elements[childIndex].compareTo(elements[childIndex + 1]) < 0) {
childIndex = childIndex + 1;//找到最大的一个儿子
}
if (rootValue.compareTo(elements[childIndex]) > 0) {//当前节点大于最大的儿子节点。
break;
} else {
elements[parentIndex] = elements[childIndex];//和儿子节点进行替换。
parentIndex = childIndex;
}
}
elements[parentIndex]=rootValue;
}
@Test
public void createHeap() {
HeapStruct heapStruct = HeapUtil.initHeap(20);
for (int i = 0; i < 11; i++) {
heapStruct.getElements()[i] = i;//初始化一个数组。
}
for (int n = (heapStruct.getSize() - 1) / 2; n >= 0; n--) {//一个个遍历父节点,使得当前父节点所在的子树变成一个堆
HeapUtil.percDown(heapStruct, n);
}
}