7月7日
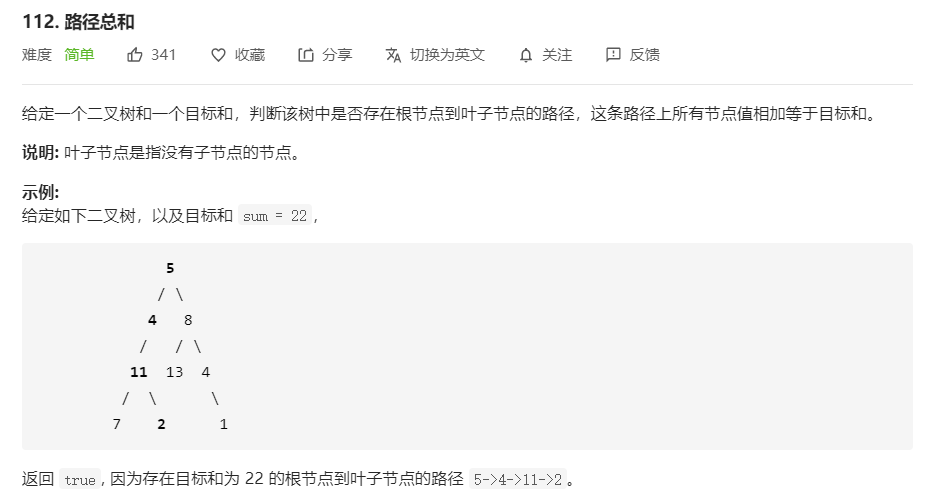
题目
我的思路
相当于遍历原树的同时新建一颗形状相同的“和树”。若和树叶子结点的val等于目标sum,则返回成功,否则返回失败。
递归过程
递归函数的作用是,输入当前原树中的某个节点和“和树”中对应的节点,返回该节点下是否存在满足要求的路径(树根到叶子结点)。
bool check(TreeNode * originalNode,TreeNode* sumNode)
- 出口条件
- 输入的原树节点没有子节点。返回当前路径是否按足要求(和树对应节点的val是否等于目标sum)true/false
- 递推过程
- 为原树节点的子节点创建在“和树”中对应的节点
- 依次原树子节点进行check
- 回溯过程
- 对本级递归调用的返回值进行判断处理,并把判断结果返回给上一级的递归调用
- 回溯返回值
- 返回当前节点下是否有满足条件的的路径。(若子节点check返回1则有,否则无)
我的实现
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: bool hasPathSum(TreeNode* root, int sum) { if(root==NULL )return false;//还要考虑原树根是null的情况。。。 //if(root==NULL && sum==0)return true; TreeNode * sumTreeRoot = new TreeNode(root->val); TreeNode * sumTreeNode = sumTreeRoot;//和树树根 int c = check(root,sumTreeNode,sum); if(c==1)return true; else return false; } bool check(TreeNode * originalNode,TreeNode * sumNode,int sum){ //printf("Original:%d Sum:%d ",originalNode->val,sumNode->val); bool checker1 = false;bool checker2=false; if(originalNode->left!=NULL){ TreeNode* newsumNode1 = addLeftSon((originalNode->left)->val+sumNode->val,sumNode); checker1 = check(originalNode->left,newsumNode1,sum); } if(originalNode->right!=NULL){ TreeNode* newsumNode2 = addRightSon((originalNode->right)->val+sumNode->val,sumNode); checker2 = check(originalNode->right,newsumNode2,sum); } if(originalNode->left==NULL&&originalNode->right==NULL&&sumNode->val==sum){ return true;} return checker1 || checker2; } TreeNode * addLeftSon(int val,TreeNode * node){ TreeNode * sonNode = new TreeNode(val); node->left = sonNode; return sonNode; } TreeNode * addRightSon(int val,TreeNode * node){ TreeNode * sonNode = new TreeNode(val); node->right = sonNode; return sonNode; } }; // /* 需要一颗与原二叉树相同的树来存储截止到当前节点的路径和 1.若存在左子节点,和树新增左子节点,和为当前和树节点的sum+left.val; 1.1check(OriginalTreeNode,SumTreeNode); 2.若存在右子节点。。。同上 n.若不存在左子节点和右子节点,比较当前和树的sum与目标和,若相同,返回1;否则返回no; **/
第一次刷题,本觉得题目很简单,但提交了5次才通过,前后更是花了一个半小时。
有以下逻辑考虑不细致的地方,以后尽量避免:
- 我采用的应该算是深搜的方法,当一条路径被否决回退时,要保证走另一条分支时的参数不受已走过的被否决分支影响。
- 当前节点是叶子节点的条件应当与当前节点存在子节点的条件互斥。最后处理的情况前少了判断条件。
- 没有考虑题目给的树根节点是NULL的情况。
拓展学习
递归
同样是递归,我的实现累赘。
class Solution { public: bool hasPathSum(TreeNode *root, int sum) { if (root == nullptr) { return false; } if (root->left == nullptr && root->right == nullptr) { return sum == root->val; } return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val); } }; /** 作者:LeetCode-Solution 链接:https://leetcode-cn.com/problems/path-sum/solution/lu-jing-zong-he-by-leetcode-solution/ 来源:力扣(LeetCode) */
- 不需要单独一颗“和树”。“和树”的作用是记录不同路径的路径总和,利用递归的传参可以记录到当前节点的路径总和,甚至可以用减法,每次递归调用时,把剩余路径和减去当前节点val的差作为参数(剩余路径和)。
- 递归函数中把出口条件的优先判断处理,可能代码更简练。

另一种思路:广度优先搜索
class Solution { public: bool hasPathSum(TreeNode *root, int sum) { if (root == nullptr) { return false; } queue<TreeNode *> que_node; queue<int> que_val; que_node.push(root); que_val.push(root->val); while (!que_node.empty()) { TreeNode *now = que_node.front(); int temp = que_val.front(); que_node.pop(); que_val.pop(); if (now->left == nullptr && now->right == nullptr) { if (temp == sum) return true; continue; } if (now->left != nullptr) { que_node.push(now->left); que_val.push(now->left->val + temp); } if (now->right != nullptr) { que_node.push(now->right); que_val.push(now->right->val + temp); } } return false; } }; /** 作者:LeetCode-Solution 链接:https://leetcode-cn.com/problems/path-sum/solution/lu-jing-zong-he-by-leetcode-solution/ 来源:力扣(LeetCode) */
- 广度优先搜索用队列实现。个人理解这里队列先进先出的特性与广搜一层一层扫描的特点吻合。
- queue<>的使用(详细原理待学习)
