台州学院we are without brain 训练 计算几何

 

 

A - View Angle

Flatland has recently introduced a new type of an eye check for the driver's licence. The check goes like that: there is a plane with mannequins standing on it. You should tell the value of the minimum angle with the vertex at the origin of coordinates and with all mannequins standing inside or on the boarder of this angle.

As you spend lots of time "glued to the screen", your vision is impaired. So you have to write a program that will pass the check for you.

Input

The first line contains a single integer n (1 ≤ n ≤ 10⁵) — the number of mannequins.

Next n lines contain two space-separated integers each: x_i, y_i (|x_i|, |y_i| ≤ 1000) — the coordinates of the i-th mannequin. It is guaranteed that the origin of the coordinates has no mannequin. It is guaranteed that no two mannequins are located in the same point on the plane.

Output

Print a single real number — the value of the sought angle in degrees. The answer will be considered valid if the relative or absolute error doesn't exceed 10^- 6.

Examples

Input

2
2 0
0 2

Output

90.0000000000

Input

3
2 0
0 2
-2 2

Output

135.0000000000

Input

4
2 0
0 2
-2 0
0 -2

Output

270.0000000000

Input

2
2 1
1 2

Output

36.8698976458

Note

Solution for the first sample test is shown below:

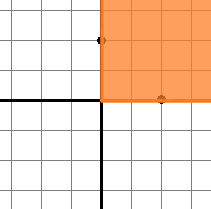
Solution for the second sample test is shown below:

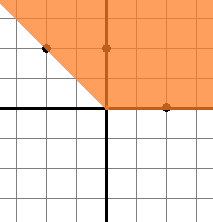
Solution for the third sample test is shown below:

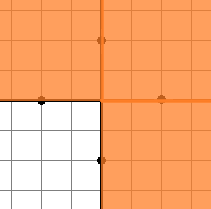
Solution for the fourth sample test is shown below:

 

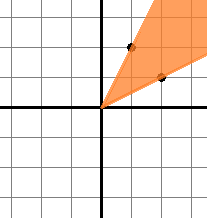
就是给你一个二维平面的若干个点，让你选一个视角可以看到所有的点

我们可以考虑一下只有两个点的情况，就是最后一个点和第一个点形成的角度，另外的就是相邻两个的角度，但是要反着来啊，也就是补角。

我自己还傻乎乎的用atan写了一下atan2的实现

#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
const double PI=acos(-1.);
const int N=1e5+5;
double a[N],x,y;
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0; i<n; i++)scanf("%lf%lf",&x,&y),a[i]=180*atan2(x,y)/PI;
    sort(a,a+n);
    double ans=a[n-1]-a[0];
    for(int i=1; i<n; i++)ans=min(ans,360+a[i-1]-a[i]);
    printf("%.12f",ans);
    return 0;
}

B - Ghosts

Ghosts live in harmony and peace, they travel the space without any purpose other than scare whoever stands in their way.

There are nn ghosts in the universe, they move in the OXYOXY plane, each one of them has its own velocity that does not change in time: V→=Vxi→+Vyj→V→=Vxi→+Vyj→ where VxVx is its speed on the xx-axis and VyVy is on the yy-axis.

A ghost ii has experience value EXiEXi, which represent how many ghosts tried to scare him in his past. Two ghosts scare each other if they were in the same cartesian point at a moment of time.

As the ghosts move with constant speed, after some moment of time there will be no further scaring (what a relief!) and the experience of ghost kind GX=∑ni=1EXiGX=∑i=1nEXiwill never increase.

Tameem is a red giant, he took a picture of the cartesian plane at a certain moment of time TT, and magically all the ghosts were aligned on a line of the form y=a⋅x+by=a⋅x+b. You have to compute what will be the experience index of the ghost kind GXGX in the indefinite future, this is your task for today.

Note that when Tameem took the picture, GXGX may already be greater than 00, because many ghosts may have scared one another at any moment between [−∞,T][−∞,T].

Input

The first line contains three integers nn, aa and bb (1≤n≤2000001≤n≤200000, 1≤|a|≤1091≤|a|≤109, 0≤|b|≤1090≤|b|≤109) — the number of ghosts in the universe and the parameters of the straight line.

Each of the next nn lines contains three integers xixi, VxiVxi, VyiVyi (−109≤xi≤109−109≤xi≤109, −109≤Vxi,Vyi≤109−109≤Vxi,Vyi≤109), where xixi is the current xx-coordinate of the ii-th ghost (and yi=a⋅xi+byi=a⋅xi+b).

It is guaranteed that no two ghosts share the same initial position, in other words, it is guaranteed that for all (i,j)(i,j) xi≠xjxi≠xj for i≠ji≠j.

Output

Output one line: experience index of the ghost kind GXGX in the indefinite future.

Examples

Input

4 1 1
1 -1 -1
2 1 1
3 1 1
4 -1 -1

Output

8

Input

3 1 0
-1 1 0
0 0 -1
1 -1 -2

Output

6

Input

3 1 0
0 0 0
1 0 0
2 0 0

Output

0

Note

There are four collisions (1,2,T−0.5)(1,2,T−0.5), (1,3,T−1)(1,3,T−1), (2,4,T+1)(2,4,T+1), (3,4,T+0.5)(3,4,T+0.5), where (u,v,t)(u,v,t) means a collision happened between ghosts uu and vv at moment tt. At each collision, each ghost gained one experience point, this means that GX=4⋅2=8GX=4⋅2=8.

In the second test, all points will collide when t=T+1t=T+1.

The red arrow represents the 1-st ghost velocity, orange represents the 2-nd ghost velocity, and blue represents the 3-rd ghost velocity.

这个题他们在群里讨论过，其实就是直接去做差，也就是a*vx-vy的值的问题，经过一次这个点也要+1

但是ans要爆int的，这个加起来就是等差数列求和

#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const double PI=acos(-1.);
map<ll,int>M;
map<pair<int,int>,int>F;
int main()
{
    int n,a,b;
    long long ans=0,t=0;
    scanf("%d%d%d",&n,&a,&b);
    for(int i=0,x,vx,vy; i<n; i++)
    {
        scanf("%d%d%d",&x,&vx,&vy);
        ans+=M[a*1LL*vx-vy]++;
        t+=F[make_pair(vx,vy)]++;
    }
    printf("%lld",2*(ans-t));
    return 0;
}