Codeforces Round #432 (Div. 2, based on IndiaHacks Final Round 2017)

昨晚打得小号，虽然很菜，可是还是涨了些rating

A. Arpa and a research in Mexican wave

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Arpa is researching the Mexican wave.

There are n spectators in the stadium, labeled from 1 to n. They start the Mexican wave at time 0.

• At time 1, the first spectator stands.
• At time 2, the second spectator stands.
• ...
• At time k, the k-th spectator stands.
• At time k + 1, the (k + 1)-th spectator stands and the first spectator sits.
• At time k + 2, the (k + 2)-th spectator stands and the second spectator sits.
• ...
• At time n, the n-th spectator stands and the (n - k)-th spectator sits.
• At time n + 1, the (n + 1 - k)-th spectator sits.
• ...
• At time n + k, the n-th spectator sits.

Arpa wants to know how many spectators are standing at time t.

Input

The first line contains three integers n, k, t (1 ≤ n ≤ 109, 1 ≤ k ≤ n, 1 ≤ t < n + k).

Output

Print single integer: how many spectators are standing at time t.

Examples

input

10 5 3

output

3

input

10 5 7

output

5

input

10 5 12

output

3

Note

In the following a sitting spectator is represented as -, a standing spectator is represented as ^.

• At t = 0  ----------  number of standing spectators = 0.
• At t = 1  ^---------  number of standing spectators = 1.
• At t = 2  ^^--------  number of standing spectators = 2.
• At t = 3  ^^^-------  number of standing spectators = 3.
• At t = 4  ^^^^------  number of standing spectators = 4.
• At t = 5  ^^^^^-----  number of standing spectators = 5.
• At t = 6  -^^^^^----  number of standing spectators = 5.
• At t = 7  --^^^^^---  number of standing spectators = 5.
• At t = 8  ---^^^^^--  number of standing spectators = 5.
• At t = 9  ----^^^^^-  number of standing spectators = 5.
• At t = 10 -----^^^^^  number of standing spectators = 5.
• At t = 11 ------^^^^  number of standing spectators = 4.
• At t = 12 -------^^^  number of standing spectators = 3.
• At t = 13 --------^^  number of standing spectators = 2.
• At t = 14 ---------^  number of standing spectators = 1.
• At t = 15 ----------  number of standing spectators = 0.

这个题我还看了两三分钟，发现就是个分段函数，结论很明显

不过我竟脑残打错了字母，wa了一发

#include<bits/stdc++.h>
using namespace std;
int main()
{
    long long n,k,t;
    cin>>n>>k>>t;
    if(t<=k)
        cout<<t<<endl;
    else if(t>=n)
        cout<<n+k-t<<endl;
    else cout<<k<<endl;
    return 0;
}

B. Arpa and an exam about geometry

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Arpa is taking a geometry exam. Here is the last problem of the exam.

You are given three points a, b, c.

Find a point and an angle such that if we rotate the page around the point by the angle, the new position of a is the same as the old position of b, and the new position of b is the same as the old position of c.

Arpa is doubting if the problem has a solution or not (i.e. if there exists a point and an angle satisfying the condition). Help Arpa determine if the question has a solution or not.

Input

The only line contains six integers ax, ay, bx, by, cx, cy (|ax|, |ay|, |bx|, |by|, |cx|, |cy| ≤ 109). It's guaranteed that the points are distinct.

Output

Print "Yes" if the problem has a solution, "No" otherwise.

You can print each letter in any case (upper or lower).

Examples

input

0 1 1 1 1 0

output

Yes

input

1 1 0 0 1000 1000

output

No

Note

In the first sample test, rotate the page around (0.5, 0.5) by .

In the second sample test, you can't find any solution.

 这个也简单，给你三个点，让你判断a，b能不能绕着一个点转到b，c的位置，明显就是等腰三角形嘛

但是不能共线，这个自己也fst了，比较好的做法是判断b不是中点

 #include<bits/stdc++.h>
using namespace std;
int main()
{
    long long ax,ay,bx,by,cx,cy;
    cin>>ax>>ay>>bx>>by>>cx>>cy;
    long long a=(ax-bx)*(ax-bx)+(ay-by)*(ay-by);
    long long b=(cx-bx)*(cx-bx)+(cy-by)*(cy-by);
    if(a==b&&(cx+ax!=2*bx||cy+ay!=2*by))
    puts("Yes");
    else puts("No");
    return 0;
}

 我现在发现是我斜率公式交换的时候写错了啊，改了字母就过了。我好菜啊

#include<bits/stdc++.h>
using namespace std;
int main()
{
    long long ax,ay,bx,by,cx,cy;
    cin>>ax>>ay>>bx>>by>>cx>>cy;
    if((ax-bx)*(ax-bx)+(ay-by)*(ay-by)==(cx-bx)*(cx-bx)+(cy-by)*(cy-by)&&(cy-ay)*(bx-ax)!=(by-ay)*(cx-ax))
    puts("Yes");
    else puts("No");
    return 0;
}

C. Five Dimensional Points

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given set of n points in 5-dimensional space. The points are labeled from 1 to n. No two points coincide.

We will call point a bad if there are different points b and c, not equal to a, from the given set such that angle between vectors 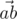 and 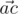 is acute (i.e. strictly less than 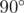). Otherwise, the point is called good.

The angle between vectors 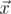 and 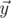 in 5-dimensional space is defined as 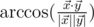, where  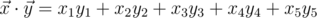is the scalar product and  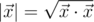is length of .

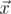Given the list of points, print the indices of the good points in ascending order.

Input

The first line of input contains a single integer n (1 ≤ n ≤ 103) — the number of points.

The next n lines of input contain five integers ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103)  — the coordinates of the i-th point. All points are distinct.

Output

First, print a single integer k — the number of good points.

Then, print k integers, each on their own line — the indices of the good points in ascending order.

Examples

input

6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1

output

1
1

input

3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0

output

0

Note

In the first sample, the first point forms exactly a 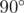 angle with all other pairs of points, so it is good.

In the second sample, along the cd plane, we can see the points look as follows:

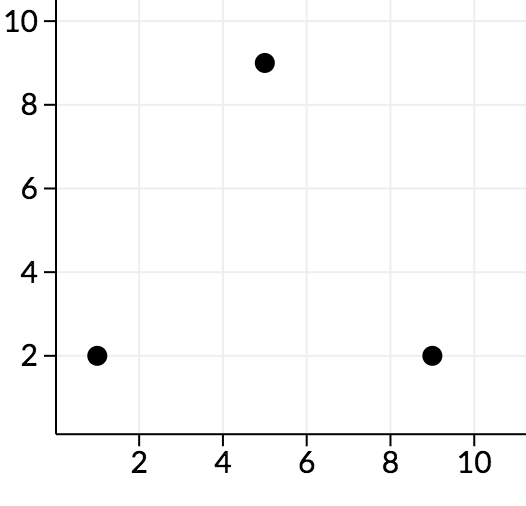
We can see that all angles here are acute, so no points are good.

给了五维坐标系，拿出了累似二维的东西，但是1e9可以跑下来么，这时候qls给了一个243的结论牛逼啊

这个题自己写错了break条件导致写了太久了，虽然中途还看了B，但是这个题分数已经掉光了

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5;
double PI=acos(0.0);
struct Point
{
    int a,b,c,d,e;
} f[250];
int main()
{
    int n;
    scanf("%d",&n);
    if(n>500)
        printf("0
");
    else
    {
        for(int i=0; i<n; i++)
            scanf("%d%d%d%d%d",&f[i].a,&f[i].b,&f[i].c,&f[i].d,&f[i].e);
        vector<int>V;
        for(int i=0; i<n; i++)
        {
            int ff=0;
            for(int j=0; j<n; j++)
            {

                Point x;
                if(j==i)continue;
                x.a=f[j].a-f[i].a;
                x.b=f[j].b-f[i].b;
                x.c=f[j].c-f[i].c;
                x.d=f[j].d-f[i].d;
                x.e=f[j].e-f[i].e;
                for(int k=0; k<n; k++)
                {
                    Point y;
                    if(j==i||k==j)continue;
                    y.a=f[k].a-f[i].a;
                    y.b=f[k].b-f[i].b;
                    y.c=f[k].c-f[i].c;
                    y.d=f[k].d-f[i].d;
                    y.e=f[k].e-f[i].e;
                    int z=y.a*x.a+y.b*x.b+y.c*x.c
                          +y.d*x.d+y.e*x.e;
                    if(z>0)
                    {
                        ff=1;
                        break;
                    }
                }
                if(ff)break;
            }
            if(!ff)
            V.push_back(i+1);
        }
        printf("%d
",(int)V.size());
        for(int i=0; i<(int)V.size(); i++)
            printf("%d
",V[i]);
    }
    return 0;
}