说好暑假刷刷CF的题提高一下的，结果自己总是忘记，其实还是懈怠，这样下去一个暑假可能什么也学不会的，随手开套CF多好啊，所以我的博客慢慢成了流水账，激励自己持续打题
Andryusha is an orderly boy and likes to keep things in their place.
Today he faced a problem to put his socks in the wardrobe. He has n distinct pairs of socks which are initially in a bag. The pairs are numbered from 1 to n. Andryusha wants to put paired socks together and put them in the wardrobe. He takes the socks one by one from the bag, and for each sock he looks whether the pair of this sock has been already took out of the bag, or not. If not (that means the pair of this sock is still in the bag), he puts the current socks on the table in front of him. Otherwise, he puts both socks from the pair to the wardrobe.
Andryusha remembers the order in which he took the socks from the bag. Can you tell him what is the maximum number of socks that were on the table at the same time?
The first line contains the single integer n (1 ≤ n ≤ 105) — the number of sock pairs.
The second line contains 2n integers x1, x2, ..., x2n (1 ≤ xi ≤ n), which describe the order in which Andryusha took the socks from the bag. More precisely, xi means that the i-th sock Andryusha took out was from pair xi.
It is guaranteed that Andryusha took exactly two socks of each pair.
Print single integer — the maximum number of socks that were on the table at the same time.
1
1 1
1
3
2 1 1 3 2 3
2
In the first example Andryusha took a sock from the first pair and put it on the table. Then he took the next sock which is from the first pair as well, so he immediately puts both socks to the wardrobe. Thus, at most one sock was on the table at the same time.
In the second example Andryusha behaved as follows:
- Initially the table was empty, he took out a sock from pair 2 and put it on the table.
- Sock (2) was on the table. Andryusha took out a sock from pair 1 and put it on the table.
- Socks (1, 2) were on the table. Andryusha took out a sock from pair 1, and put this pair into the wardrobe.
- Sock (2) was on the table. Andryusha took out a sock from pair 3 and put it on the table.
- Socks (2, 3) were on the table. Andryusha took out a sock from pair 2, and put this pair into the wardrobe.
- Sock (3) was on the table. Andryusha took out a sock from pair 3 and put this pair into the wardrobe.
你有n双袜子，但是你要拿袜子，肯定是从中一只一只拿，拿到了就放到衣柜里，问你桌面上最多会有几双袜子
所以用set维护起来就很简单了
#include <bits/stdc++.h> using namespace std; int main(){ int n; cin>>n; n*=2; set<int>S; int ma=0; for(int i=0;i<n;i++){ int x; scanf("%d",&x); if(S.count(x)){ S.erase(x); } else S.insert(x); ma=max((int)S.size(),ma); } cout<<ma<<endl; return 0;}
The main road in Bytecity is a straight line from south to north. Conveniently, there are coordinates measured in meters from the southernmost building in north direction.
At some points on the road there are n friends, and i-th of them is standing at the point xi meters and can move with any speed no greater than vi meters per second in any of the two directions along the road: south or north.
You are to compute the minimum time needed to gather all the n friends at some point on the road. Note that the point they meet at doesn't need to have integer coordinate.
The first line contains single integer n (2 ≤ n ≤ 60 000) — the number of friends.
The second line contains n integers x1, x2, ..., xn (1 ≤ xi ≤ 109) — the current coordinates of the friends, in meters.
The third line contains n integers v1, v2, ..., vn (1 ≤ vi ≤ 109) — the maximum speeds of the friends, in meters per second.
Print the minimum time (in seconds) needed for all the n friends to meet at some point on the road.
Your answer will be considered correct, if its absolute or relative error isn't greater than 10 - 6. Formally, let your answer be a, while jury's answer be b. Your answer will be considered correct if 
holds.
3
7 1 3
1 2 1
2.000000000000
4
5 10 3 2
2 3 2 4
1.400000000000
In the first sample, all friends can gather at the point 5 within 2 seconds. In order to achieve this, the first friend should go south all the time at his maximum speed, while the second and the third friends should go north at their maximum speeds.
这道题和WF的那道仪表盘很像，应该也是二分
就是一堆人站在x坐标轴上，有最大速度V，傻逼了，多加一位就GG，写错条件自己一直没有看到，就是向右跑，如果还跑不过第一个人向右跑就得GG或者你又向左跑，结果也跑不过第一位向右跑的
#include <bits/stdc++.h> using namespace std; const int N=60005; const int INF=1e9+7; int a[N],b[N],n; int la(double x){ double mi=a[0]-x*b[0],ma=a[0]+x*b[0]; for(int i=1;i<n;i++){ double mit=a[i]-x*b[i],mat=a[i]+x*b[i]; if(mat<mi||mit>ma)return 0; mi=max(mi,mit),ma=min(ma,mat); } return 1; } int main() { cin>>n; for(int i=0; i<n; i++) cin>>a[i]; for(int i=0; i<n; i++) cin>>b[i]; double l=0,r=INF; while((fabs(l-r))>1e-7){ double mi=(r+l)/2; if(la(mi)) r=mi; else l=mi; } printf("%.6f",l); return 0; }
Andryusha goes through a park each day. The squares and paths between them look boring to Andryusha, so he decided to decorate them.
The park consists of n squares connected with (n - 1) bidirectional paths in such a way that any square is reachable from any other using these paths. Andryusha decided to hang a colored balloon at each of the squares. The baloons' colors are described by positive integers, starting from 1. In order to make the park varicolored, Andryusha wants to choose the colors in a special way. More precisely, he wants to use such colors that if a, band c are distinct squares that a and b have a direct path between them, and b and c have a direct path between them, then balloon colors on these three squares are distinct.
Andryusha wants to use as little different colors as possible. Help him to choose the colors!
The first line contains single integer n (3 ≤ n ≤ 2·105) — the number of squares in the park.
Each of the next (n - 1) lines contains two integers x and y (1 ≤ x, y ≤ n) — the indices of two squares directly connected by a path.
It is guaranteed that any square is reachable from any other using the paths.
In the first line print single integer k — the minimum number of colors Andryusha has to use.
In the second line print n integers, the i-th of them should be equal to the balloon color on the i-th square. Each of these numbers should be within range from 1 to k.
3
2 3
1 3
3
1 3 2
5
2 3
5 3
4 3
1 3
5
1 3 2 5 4
5
2 1
3 2
4 3
5 4
3
1 2 3 1 2
In the first sample the park consists of three squares: 1 → 3 → 2. Thus, the balloon colors have to be distinct.
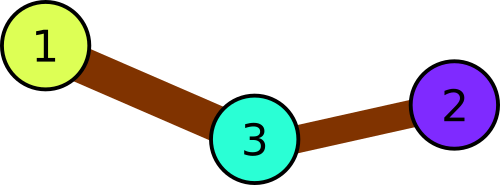Illustration for the first sample.In the second example there are following triples of consequently connected squares:
- 1 → 3 → 2
- 1 → 3 → 4
- 1 → 3 → 5
- 2 → 3 → 4
- 2 → 3 → 5
- 4 → 3 → 5
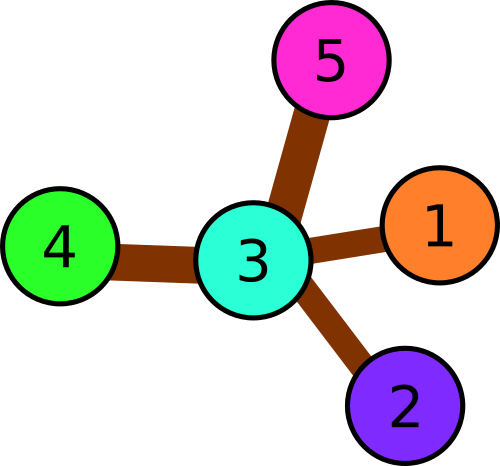Illustration for the second sample.In the third example there are following triples:
- 1 → 2 → 3
- 2 → 3 → 4
- 3 → 4 → 5
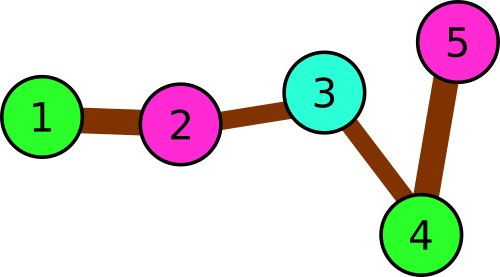Illustration for the third sample.
看起来挺复杂的，实际就是dfs一下这个图
#include <bits/stdc++.h> using namespace std; const int maxn=2e5+10; int color[maxn]; vector<int> e[maxn]; int cnt[maxn]; void dfs(int u, int fa) { int k = 1; for(int i = 0; i<e[u].size(); i++) { int v = e[u][i]; if(v==fa) continue; while(k==color[u] || (fa!=-1 && k==color[fa] )) k++; color[v] = k++; dfs(v,u); } } int main() { ios_base::sync_with_stdio(false); int n; cin>>n; int u,v; for(int i= 1; i<n; i++) { cin>>u>>v; cnt[u]++; cnt[v]++; e[u].push_back(v); e[v].push_back(u); } int ans = 0; int num; for(int i= 1; i<=n; i++) { if(cnt[i]>ans) { num = i; ans = cnt[i]; } } cout << ans +1 << endl; color[num] = 1; dfs(num,-1); for(int i = 1; i<=n; i++) cout << color[i] << " "; cout << endl; return 0; }