此博客原文地址:https://www.cnblogs.com/BobHuang/p/12654026.html
Bob老师遇到了3439: 完全平方数这个题目,他现在没啥想法。他选择去循环变量i从0到n看看是不是可以得到答案,于是写下了如下代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
//读入n
while (cin >> n)
{
//如果n为-1,结束循环
if (n == -1)
break;
//定义一个旗子,初始未插上。即n不是完全平方数
int flag = 0;
for (int i = 0; i <= n; i++)
{
//枚举的i等于n了结束循环
if (i * i == n)
{
//插上旗子,表示n是完全平方数
flag = 1;
break;
}
}
//分存在和不存在的情况
if (flag == 0)
cout << "No
";
else
cout << "Yes
";
}
return 0;
}
但是他悲伤得获得了TLE(Time Limit Exceeded),因为如果一个数不是完全平方数循环就要执行n+1次,如果是10^9^那么就要执行0^9^+1次,太慢了不能满足这个题目的要求。我们可以用大写字母O来表示时间复杂度,可以粗略的理解就是循环的次数,上述做法的算法复杂度是O(n),即线性阶(1和n比起来很小,被我们舍去了)。还有T组,那么总复杂度为O(T*n),接下来我们将优化这个做法。
一、做一些微小的优化
Alice和Bob说,你这也太傻了,有些循环完全不用运行,既然你知道i * i == n可以结束循环,那不是的时候什么时候可以循环呢。
如果是8,1 * 1 = 1 ;2 * 2 = 4;3 * 3 = 9。9已经比8大了,在找下去肯定也没有啊。Bob把下面的程序添了一个if,就通过了题目。现在我们的算法复杂度是O(T*sqrt(n)),也就是10^9^的循环我只需要31624次,因为31623 * 31623 > 10^9^。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
//读入n
while (cin >> n)
{
//如果n为-1,结束循环
if (n == -1)
break;
//定义一个旗子,初始未插上。即n不是完全平方数
int flag = 0;
for (int i = 0; i <= n; i++)
{
//枚举的i等于n了结束循环
if (i * i == n)
{
//插上旗子,表示n是完全平方数
flag = 1;
break;
}
//肯定不存在了,也要结束循环
if (i * i > n)
{
break;
}
}
//分存在和不存在的情况
if (flag == 0)
cout << "No
";
else
cout << "Yes
";
}
return 0;
}
哎呦,不错哦。如果让你求i*i<=n的i最大值呢,那我循环的时候统计ans不就好了。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
//读入n
while (cin >> n)
{
//如果n为-1,结束循环
if (n == -1)
break;
//定义答案,如果不存在为-1
int ans = -1;
for (int i = 0; i <= n; i++)
{
//枚举的i要结束了
if (i * i > n)
{
break;
}
//答案就是当前的i
ans = i;
}
//输出答案
cout << ans << "
";
}
return 0;
}
如果n很大,那么sqrt之后依旧很大,比如10^18^,还需要10^9^次,有没有更好的做法呢。
二、二分优化
Bob翻了翻自己的笔记很快想到了可以二分进行求解,他可以在log2(n)次解决,也就是1024的话10次,1024*1024只要20次,1e9也只要30次。为什么可以进行二分,他是否满足二分特性呢?
y=x^2^ 的函数图像如下所示:
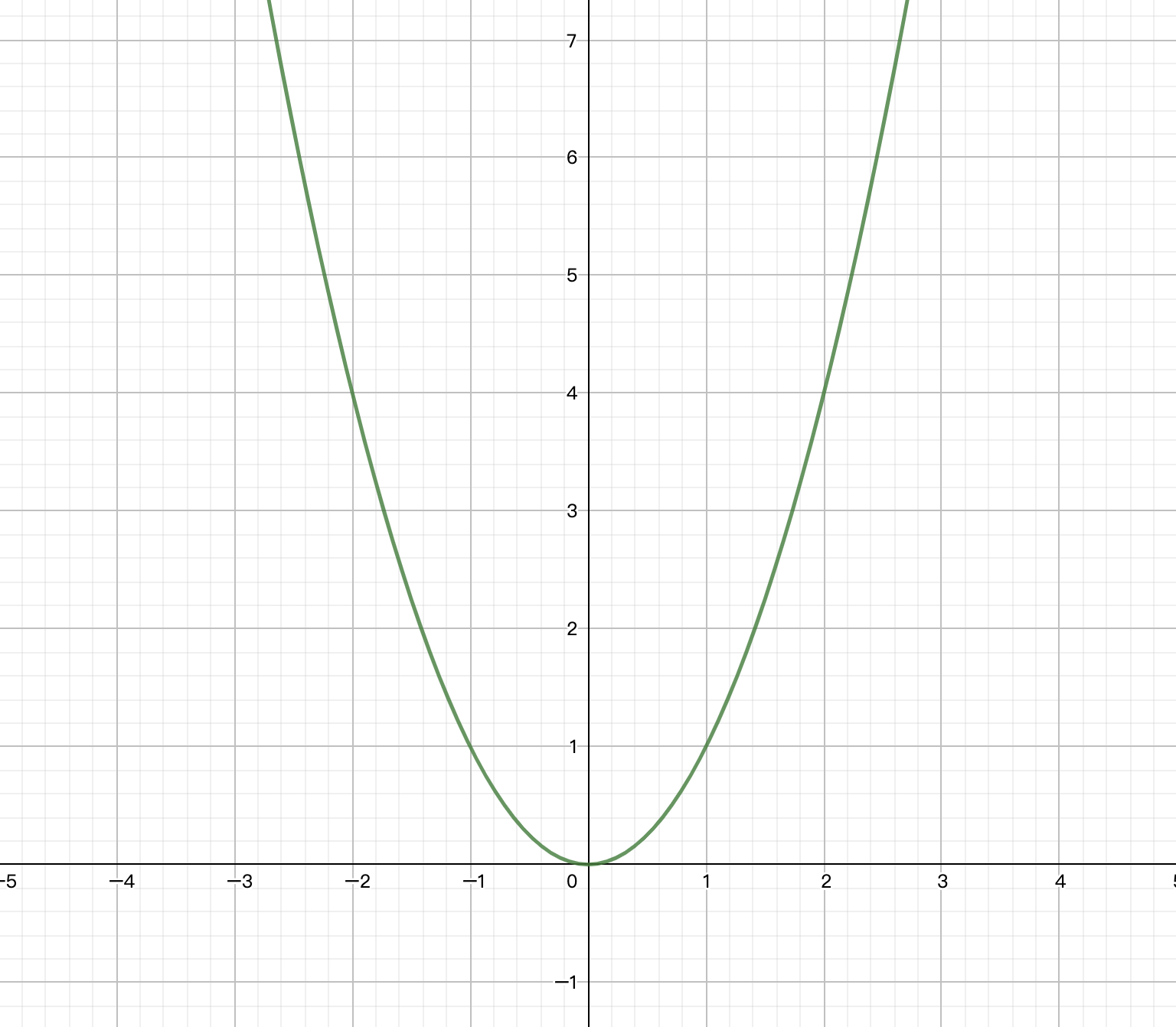
我们需要的是y值,在[0,+∞]为单调递增函数,满足单调性,所以可以二分。如果你要找[-2,100]就不能二分了,因为区间不单调,但是可以转换[-2,0]和[0,100]两段,如果是y=ax^2^+bx+c进行求y=3,左右是完全对称的,所以我们求任何一侧均可。
我们可以使用二分去解决这个问题,首先我们可以确定二分区间为0到n,然后就是找到一个点,判断在其左边还是右边的问题了。可以写出如下函数:
int HalfCalSqrt(int n)
{
//有可能<,也有可能=,ans用来存储<的
int L = 0, R = n, ans=-1;
//为什么有=,因为我们二分为闭区间
while (L <= R)
{
int Mid = (L + R) / 2;
if (Mid * Mid == n)
{
//正好为完全平方数返回
return Mid;
}
else if (Mid * Mid < n)
{
//答案可能在右边,也可能就是Mid
ans = Mid;
//继续搜索[Mid+1,R]
L = Mid + 1;
}
else
{
//答案在左边,继续搜索[L,Mid-1]
R = Mid - 1;
}
}
return ans;
}
但是输入1e9会发生什么呢,你会发现自己Mid*Mid为负数,你需要使用变量类型long long或者直接给R初始值4e4。不过二分的时候(L+R)/2还是有其他潜在bug,L+R有可能超出当前范围,成熟的OIer和ACMer会使用L+(R-L)/2来防溢出。
三、牛顿迭代优化
了解过一点微积分的同学可能想用牛顿迭代来做,高次方程没有通解,往往会使用牛顿迭代来做。这里有比较详细的牛顿迭代介绍。牛顿迭代得到的式子为
这这个题目f'(xn)指的是斜率,二次函数的切线方程为y=2x。所以这个式子为
然后我们可以写出如下代码
int NewtonMethod(int n)
{
//选择x=0和x=1的前后两项
int pre = 0, nxt = 1;
while (true)
{
/*
xn+1=xn-(xn^2-n)/(2xn)
也就是后一项为当前项减去(当前点的值)/(当前点的导数)
即nxt+(nxt*nxt-n)/(2*nxt)
化简之后如lst所示
*/
int lst = (nxt + n / nxt) / 2;
//已经收敛
if (lst == pre)
{
return pre;
}
//进行迭代
pre = nxt;
nxt = lst;
}
}
四、浮点数改造
当然如果用小数就可以少用一个变量,小数也能正确。当然有精度误差。你之后再取整可能会出问题,你可以传入x的时候+0.5,二分也可以这样。
double FloatNewtonMethod(int x)
{
//0进行特殊处理,当然负数也无法处理
if(x==0)return 0;
//取x=0和x=1这两项
double pre = 0, nxt = 1;
//迭代还没结束,当然也可以用eps进行比较
while (nxt != pre)
{
pre = nxt;
//进行迭代
nxt = (nxt + x / nxt) / 2;
}
return nxt;
}
当然二分也可以用小数,但是最终的比较可能会有问题。因为浮点数不能精确的表示,double的有效位数是15~16位。所以我们可以使用eps来控制结束
const double eps = 1e-8;
double FloatHalfCalSqrt(double n)
{
double L = 0, R = n;
//二分开区间(L,R],最终L和R"相等"。
while (fabs(L - R) >= eps)
{
double Mid = (L + R) / 2;
if (Mid * Mid >= n)
{
//答案在右边,继续搜索(Mid,R]
R = Mid;
}
else
{
//答案在左边,继续搜索(Mid+1,R]
L = Mid;
}
}
return L;
}
当然也可以通过二分次数,不断地除以2就类似于进制转换,很快就会除完。比如1e9(二进制长度为log2(1e9)=30位)连续除以2进行32次就可以精确到0.25了。二分次数也是一个很常用的做法,因为上面的代码时间复杂度在大数的时候会出问题,不是一定的。
double FloatHalfCalSqrt(double n)
{
double L = 0, R = n;
//二分100次,足够精确
for(int i=0;i<100;i++)
{
double Mid = (L + R) / 2;
if (Mid * Mid >= n)
{
//答案在右边,继续搜索
R = Mid;
}
else
{
//答案在左边,继续搜索
L = Mid;
}
}
return L;
}
如果n的数据扩充到long long呢,你会发现这个代码炸了,因为两数相乘还是double,double的有效位数只有15~16位,但是9e18是19位,所以二分求出浮点数然后在取整的方法不灵了。牛顿迭代的比较为值的比较,牛顿迭代依旧可以使用。
五、雷神之锤3的强大代码
Carmack在QUAKE3(雷神之锤3)中使用了下面的算法,它第一次在公众场合出现的时候,几乎震住了所有的人。
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
#ifndef Q3_VM
#ifdef __linux__
assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif
return y;
}
0x5f3759df这个十六进制值是不是很nb,的确是一个超级的Magic Number(魔法值)。Carmack简直是神人,经过大家的测试,这个确实比math里的sqrt更优秀。
值得注意的是,在Chris Lomont的演算中,理论上最优秀的常数(精度最高)是0x5f37642f,并且在实际测试中,如果只使用一次迭代的话,其效果也是最好的。但奇怪的是,经过两次牛顿迭代后,在该常数下解的精度将降低得非常厉害。经过实际的测试,Chris Lomont认为,最优秀的常数是0x5f375a86。如果换成64位的double版本的话,算法还是一样的,而最优常数则为0x5fe6ec85e7de30da(又一个非常厉害的Magic Number)。
用这个魔法值我们可以得到另一个做法,因为雷神之锤3的并不那么完美。
double Sqrt(float x)
{
double xhalf = 0.5 * (double)x;
//得到x的二进制位
int i = *(int *)&x;
//初始化猜的xn
i = 0x5f375a86 - (i >> 1);
//把它的二进制为转换为float
x = *(float *)&i;
//牛顿迭代, 反复进行提高精确度
x = x * (1.5f - xhalf * x * x);
x = x * (1.5f - xhalf * x * x);
x = x * (1.5f - xhalf * x * x);
return 1.0 / (double)x;
}
六、内置开平方函数
内置开平方函数为sqrt(),参数为浮点型,返回值也为浮点型。c++11前的参数支持的类型为float和double两种。c++11的类型更丰富。C++调用的是__builtin_sqrtf(x)其实他对应的是是一条内置的CPU指令,我们可以汇编出来,C语言编译出来的为
call _sqrt
C++编译出来的为
call __ZSt4sqrtIiEN9__gnu_cxx11__enable_ifIXsrSt12__is_integerIT_E7__valueEdE6__typeES3_
C++还是调用了call _sqrt ,所以其实C++编译要比c语言更慢。如果比如使用了unsinged long long类型,不使用c++11就会出现不支持,导致wa。
七、时间复杂度及时钟周期数比较
时间复杂度
- 及时break sqrt(n)
- 二分 log(n)
- 牛顿迭代 log(n),运行次数比二分少
- 倒平方 常数级别
- math函数 常数级别 指令
时钟周期比较,我用如下代码进行测试。我的CPU是2.3 GHz 双核Intel Core i5-7360U,两核心四线程,动态加速频率为3.6GHz。
#include <bits/stdc++.h>
#include <sys/time.h>
using namespace std;
const int N = (1 << 28);
long long a[N];
inline long long getCurrentTime()
{
//用于获取系统微秒时间
struct timeval tv;
gettimeofday(&tv, NULL);
return tv.tv_sec * 1000000 + tv.tv_usec;
}
double Sqrt(double x)
{
return sqrt(x);
}
int main()
{
srand(time(NULL));
//2.3GHz*10^9/10^6,得到每微秒的时钟周期数
long long t_c = 2300;
for (int k = 0; k <= 28; k += 2)
{
long long v = 1 << k;
for (int i = 0; i < v; ++i)
{
a[i] = rand()*1LL*rand();
}
long long t1 = getCurrentTime();
for (int i = 0; i < v; ++i)
{
long long j = Sqrt(a[i]);
}
long long t2 = getCurrentTime();
cout << "time:" << v << " " << t2 - t1 << " us"
<< " clocks:" << t_c * 1. * (t2 - t1) / v << '
';
}
return 0;
}
每次调用时钟周期数
- 二分 340个时钟周期
- 牛顿迭代 1086个时钟周期
- 倒平方 常数级别 0.7个时钟周期
- math函数 4个时钟周期
倒平方很快很快,Carmack太神了,但是这个0.7个时钟周期让我百思不得其解,我猜测这个牛顿迭代的过程可能被cpu优化得比较厉害,比如多核、缓存、超级流水线技术。虽然牛顿迭代运行次数与二分相比较少,但是由于二分一直再除2,可能被优化了,所以常数比较小,跑出来比牛顿迭代还要快。不过在大数里可能就不一定,Java大数用二分写可能会卡常(卡常数)。
上面可能是C++的编译器被优化了,我用C重新测试的每次调用时钟周期数如下所示:
- 二分 598个时钟周期
- 牛顿迭代 1246个时钟周期
- 倒平方 常数级别 68个时钟周期
- math函数 15个时钟周期