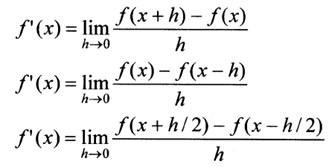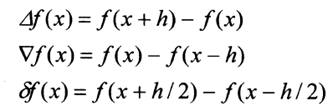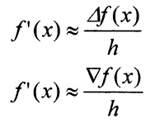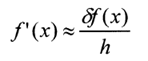(一)数值积分
一、数值积分的MATLAB实现方法:
1、变步长辛普生法(quad)法:
(1)调用格式:
[I,n]=quad('fname',a,b,tol,trace);
fname是被积函数;
a,b是积分上下限;
tol来控制积分精度,默认为0.001;
trace控制是否展现积分过程,默认为0,不展现;若trace≠0,则展现。
(2)fname使用的两种方法:
建立函数文件:
function f=fesin(x)
f=……;另一种则是使用内联函数(据说14后的版本会删除这个):
g=inline('exp(-0.5*x)',x);
2、牛顿——科特斯法
[I,n]=quad8('fname',a,b,tol,trace);
形参完全同上,但是效果比较好。
3、当被积函数只有离散解时积分的方法:
trapz(X,Y);
X,Y是等长的向量,满足Y=f(X);
二、二重定积分的数值求解
I=dblquad(f,a,b,c,d,tol,trace);
f为被积函数,同样可以有两中给出方式
a,b,c,d定义了被积区间
tol为精度
trace为是否展示过程
(二)数值微分
一、数值差分与差商
1、导数的定义:
2、差分定义:
3、差商定义:
二、数值微分的实现:
一共三种方法:
(1)使用多项式或者样条函数进行拟合,对拟合函数进行求导,得到需要点的导数
(2)使用差商作为导数
(3)如果被积函数可导,可直接求导,再带入。
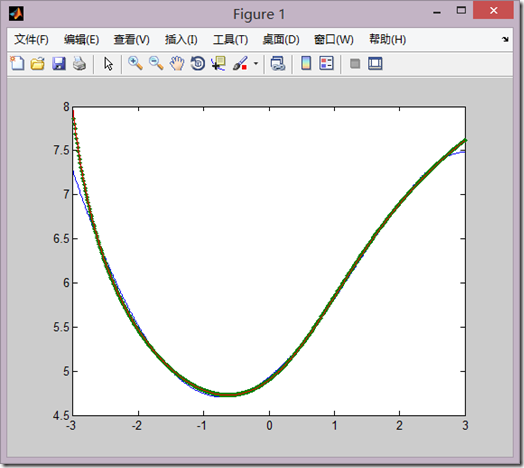
一个demo
MATLAB三种方式编程求解:
f=inline('sqrt(x.^3+2*x.^2-x+12)+(x+5).^(1/6)+5*x+2'); g=inline('(3*x.^2+4*x-1)./sqrt(x.^3+2*x.^2-x+12)/2+1/6./(x+5).^(5/6)+5'); x=-3:0.01:3; %求导数点 %方法一 p=polyfit(x,f(x),5); dp=polyder(p); dpx=polyval(dp,x); %方法二 dx=diff(f([x,3.01]))/0.01; %方法三 gx=g(x); plot(x,dpx,x,dx,'.',x,gx,'-');