PAT 1147 Heaps[难]

1147 Heaps（30 分）

In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if P is a parent node of C, then the key (the value) of P is either greater than or equal to (in a max heap) or less than or equal to (in a min heap) the key of C. A common implementation of a heap is the binary heap, in which the tree is a complete binary tree. (Quoted from Wikipedia at https://en.wikipedia.org/wiki/Heap_(data_structure))

Your job is to tell if a given complete binary tree is a heap.

Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers: M (≤ 100), the number of trees to be tested; and N (1 < N ≤ 1,000), the number of keys in each tree, respectively. Then M lines follow, each contains N distinct integer keys (all in the range of int), which gives the level order traversal sequence of a complete binary tree.

Output Specification:

For each given tree, print in a line Max Heap if it is a max heap, or Min Heap for a min heap, or Not Heap if it is not a heap at all. Then in the next line print the tree's postorder traversal sequence. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line.

Sample Input:

3 8
98 72 86 60 65 12 23 50
8 38 25 58 52 82 70 60
10 28 15 12 34 9 8 56

Sample Output:

Max Heap
50 60 65 72 12 23 86 98
Min Heap
60 58 52 38 82 70 25 8
Not Heap
56 12 34 28 9 8 15 10

 题目大意：输入几组完全二叉树的层次遍历序列，判断它是最大堆、最小堆、还是啥都不是。树中节点数N<=1000

 //如果只判断是不是堆，完全不用建树，因为是完全二叉树可以利用数组下标，左子树下标为2*i,右子树是2*i+1。然而最终都要给出来后根遍历，所以建树再后根遍历还是比较方便的。

//怎么根据层次遍历建树呢？不会也。。。

#include <iostream>
#include <string>
#include <vector>
#include<cstdio>
using namespace std;
int main() {
    int k,n;
    cin>>k>>n;
    while(k--){
        vector<int> tree(n+1);
        for(int i=1;i<=n;i++){
            cin>>tree[i];
        }
        bool flag=true;
        for(int i=1;2*i<=n||2*i+1<=n;i++){//判断是否是最大堆
            if(tree[i]>=tree[2*i]&&tree[i]>=tree[2*i+1])continue;
            else{
                flag=false;break;
            }
        }
        if(flag)cout<<"Max Heap
";
        else{
            flag=true;
            for(int i=1;2*i<=n||2*i+1<=n;i++){
            if(tree[i]<=tree[2*i]&&tree[i]<=tree[2*i+1])continue;
            else{
                flag=false;break;
            }
            }
            if(flag)cout<<"Min Heap
";
            else cout<<"Not Heap
";
        }
    }

    return 0;
}

写出的这个代码在运行样例的时候，出现了以下问题：

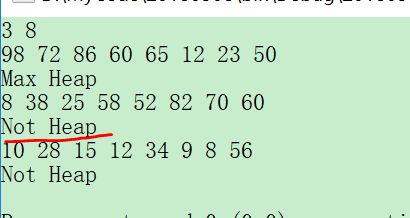
第二个最小堆，判断不是最小堆，突然发现是因为代码里，寻址了不存在的单元！这样的话那个单元是一个很大的负值，那么最大堆当然是可以判断了，但是最小堆就出现了问题！

//那如果那样去判断的话，可就是很复杂了。。。放弃。

//看到大佬28行的代码，内心是震惊的。。

 代码来自:https://www.liuchuo.net/archives/4667

#include <iostream>
#include <vector>
using namespace std;
int m, n;
vector<int> v;
void postOrder(int index) {//原来可以根据下标遍历完全二叉树啊！
    if (index >= n) return;
    postOrder(index * 2 + 1);
    postOrder(index * 2 + 2);//就算index * 2 + 2那么就会return,正好是递归出口。
    printf("%d%s", v[index], index == 0 ? "
" : " ");
    //如果遍历到最终根节点即index=0，那么
}
int main() {
    scanf("%d%d", &m, &n);
    v.resize(n);//其实完全可以只用一个向量，因为新输入的会将原来的覆盖。
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) scanf("%d", &v[j]);
        int flag = v[0] > v[1] ? 1 : -1;//根据这个判断可能的情况。
        for (int j = 0; j <= (n-1) / 2; j++) {//原来可以这样限制j的范围。
            int left = j * 2 + 1, right = j * 2 + 2;
            //因为只有右边的会超，所以只控制右边即可。
            //厉害了，反过来进行判断。
            if (flag == 1 && (v[j] < v[left] || (right < n && v[j] < v[right]))) flag = 0;
            if (flag == -1 && (v[j] > v[left] || (right < n && v[j] > v[right]))) flag = 0;
        }
        if (flag == 0) printf("Not Heap
");
        else printf("%s Heap
", flag == 1 ? "Max" : "Min");//这一句厉害厉害。
        postOrder(0);
    }
    return 0;
}

//真是太厉害了，再判断是否是堆以及后根遍历的时候，我还需要时间消化