1.数据压缩
数据压缩不仅能够减小存储空间,并且能够加速学习算法。那么什么是数据压缩呢?下面给出了一个简单的例子:

图1.数据压缩的概念
举了两个例子,一个是横轴x1是厘米,纵轴特征x2是英尺,这明显是冗余的,但是在真正的实施过程中,这并不常见,这并不是一个好例子。
另一个例子是,横轴是驾驶员的技术,纵轴是驾驶员的快乐程度,曲线的含义是驾驶员的能力,那么比较明显的是,可以舍去驾驶员的快乐程度这个特征。即将数据集从2维转向1维。

图2.二维数据压缩
在图中,将绿线投影到一个轴上,那么如果点的排列方式能够一一对应,并且反映原来的顺序,那么就可以用其中一个特征来表示两个,从x(1)二维转换到z(1)一维,从而实现了数据压缩。这种方法能让算法运行的更快,同时也能够减少数据存储空间。

图2.三维数据压缩
在实际中,有将1000维压缩到100维的,但是不方便进行画图展示。如图中,三维的可以观察出数据基本上同一平面内,所以图2中就新构建了一个二维的平面图,将数据都投影到二维平面上,将三维降低到二维。
2.可视化
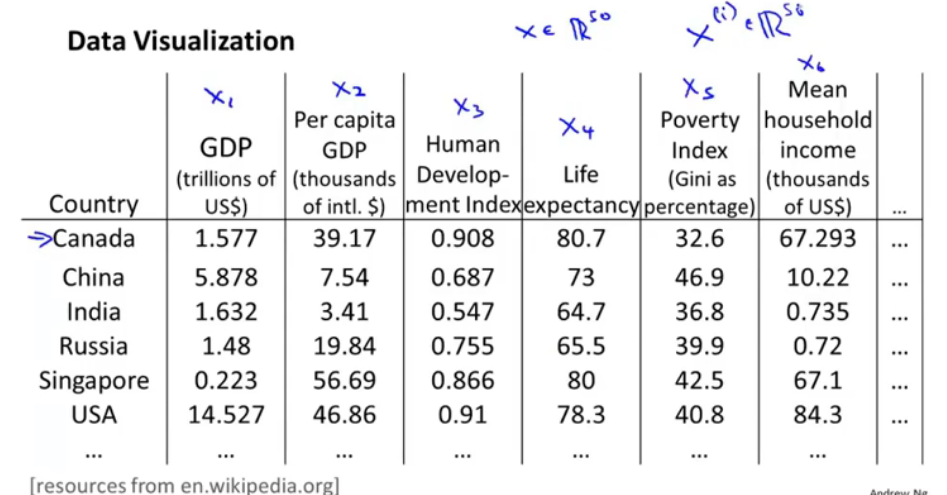
图3.高维数据
比如得到了各个国家的一个高维数据图,有很多指标,那么如何来进行可视化呢?如下图,选取几个指标来表示国家,比如两个:

图4.二维数据可视化
比如横轴表示国家的大小/GDP,纵轴表示,人均GDP的数量,从图中可对点进行现实意义的分析。
3.主成分分析问题规划1
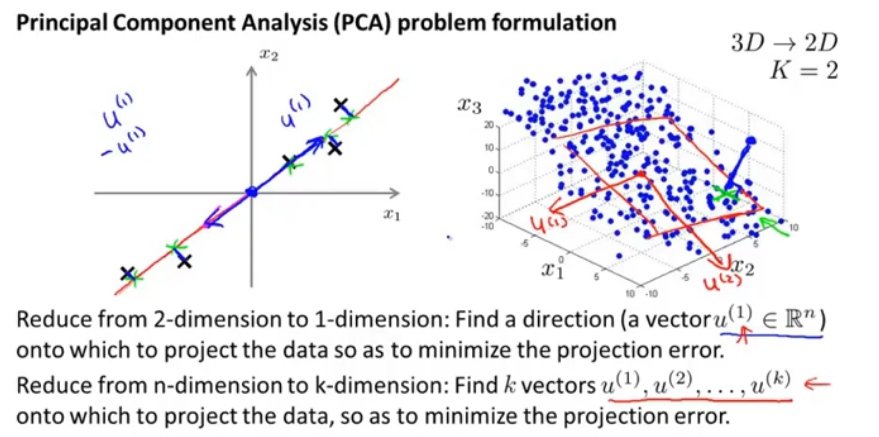
图5.主成分问题规划
将数据从二维到一维,需要找到一个向量的方向,将其他点投影,这个方向是满足最小化投影误差。那么就可将数据降维。
从三维降到二维,需要两个投影向量组成一个平面,将其他点投影,作最小化投影误差。
从n维降到k维,就需要选k个向量进行投影,并且最小化投影误差。
那么从左图中看,PCA似乎和线性回归很像,那么二者之间有何关系呢?
实际两者是完全不同的算法,PCA是找到一个低维的平面进行数据的投影,以便最小化投影误差。
4.主成分分析问题规划2

图6.数据预处理
首先求出m个数据的均值每个维度的均值,并且对i个数据,每个对应的维度都变成平均的,图中下边给的公式是在有监督学习中,每个数据的i维-均值,并且除以s_j,通常是max-min或者是均方误差。这样让不同含义的数据都能够进行归一,又可以比较的值。

图7.主成分分析算法
首先,第一个公式中,左边的Σ不是求和符号,而是表示矩阵,那么它是一个n*n的矩阵,也就是协方差矩阵。
然后再计算协方差矩阵Σ的特征向量,可以使用svd函数。令协方差矩阵是正定矩阵。现在就可以用[U,S,V]是用svd命令来计算协方差矩阵。
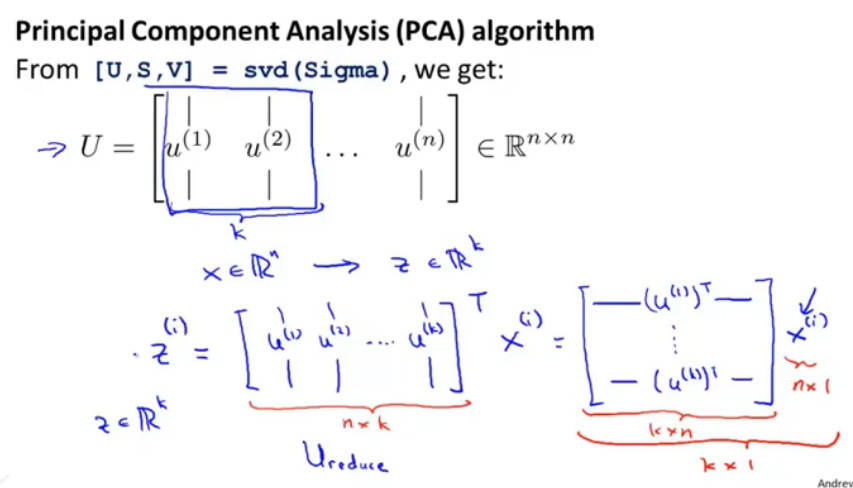
图8.算法
取U的前k列,得到一个U_reduce是n*k的,那么用它的T*训练集中的每个x,最终会得到一个k维的向量,这个就是投影压缩之后的。