ch5图
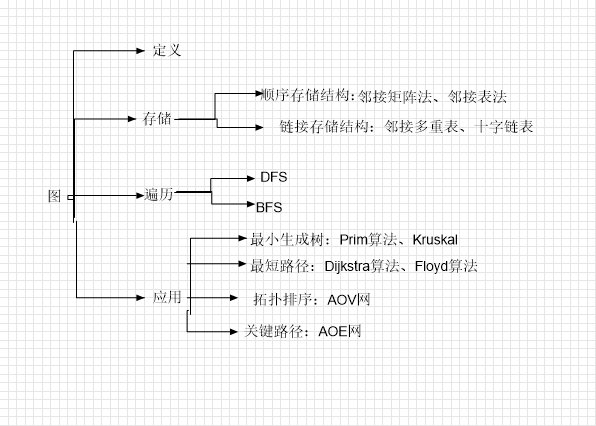
1.图的定义和基本概念
定义:G=(V,E),V是图G中的顶点的有限非空集;E是图G中顶点之间的关系(边)集合。V一定非空。
基本概念:
有向图、无向图、简单图、多重图、完全图、子图、连通图、连通分量、强连通图、强连通分量、生成树、生成森林、度(无向图)、入出度(有向图)、边的权和网、路径、路径长度。
无向图:连通(顶点v到顶点w有路径存在),连通图(图中任意两个顶点都是连通的)。
有向图:强连通(顶点v到顶点w和顶点w到顶点v都有路径存在),强连通图(任何一对顶点都是强连通的)。
路径长度:路径上边的数目。
2.图的存储以及基本操作
1)顺序存储结构:邻接矩阵、邻接表
邻接矩阵法:vi到vj有边相连,则A[i][j]为1,否则为0;适合稠密图。
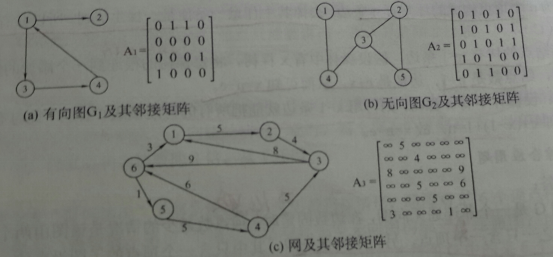
邻接表法:适合稀疏图。

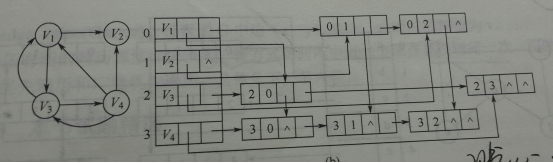
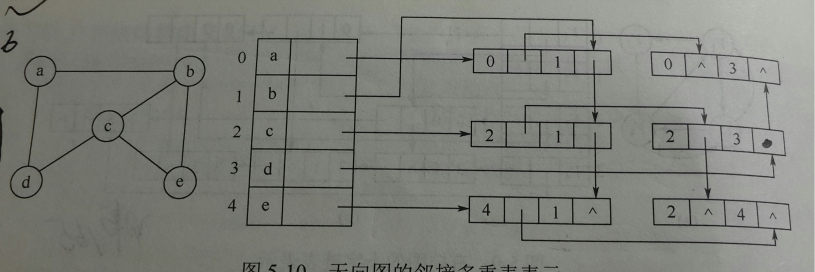
2)链式存储结构:十字链表、邻接多重表
十字链表:是有向图的一种链式存储结构。
邻接多重表:是无向图的一种链式存储结构。
3)图的基本操作
比如判断图G是否存在边<x,y>,列出图G中与结点x邻接的边,在图G中插入(删除)顶点x,从图中删除或者添加某边等等。
3.图的遍历
1)BFS(Breadth-First-Search)
是一种分层查找的过程,借助辅助队列。(图的BFS与二叉树的层序遍历完全一致)
基本思想:首先访问顶点v,接着访问v各个未被访问过的邻接顶点w1、w2、w3、、、、;然后再依次访问w1各个未被访问过的邻接顶点,再依次访问w2各个未被访问过的邻接顶点,、、、;再从这些访问过的顶点出发,再访问它们所有未被访问过的邻接顶点、、、、以此类推,一直到图中所有的顶点都被访问过为止。
无论是存储方式是邻接矩阵(顺序存储)还是邻接表(链式存储),BFS都需要借助一个辅助队列Q,n个顶点都需要入队一次,在最坏情况下,空间复杂度是O(V)。
当采用邻接表的存储方式时,每个顶点均需要搜索一次(或入队一次),故时间复杂度为O(V),在搜索任一顶点的邻接点时,每条边至少访问一次,故时间复杂度为O(E),故算法的总时间复杂度是O(V+E)。
当采用邻接矩阵的存储方式时,查找每个顶点的邻接点所需时间为O(V),故算法总时间复杂度为O(V*V)。
BFS算法求解单源最短路径问题,广度优先生成树问题。
2)DFS(Depth-First-Search)
类似于树的先序遍历,用到递归,借助递归工作栈,空间复杂度为O(V)。遍历图的实质上是对每个顶点查找其邻接点的过程,其耗费的时间取决于所采用的存储结构。
基本思想:首先访问顶点v,然后由v出发,访问与v邻接且未被访问的任一顶点w1,再访问与w1邻接且未被访问的任一顶点w2,。。。。重复以上过程。当不能再继续向下访问时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问过,则从该点继续上述搜索过程,直到图中所有顶点均被访问过为止。
当以邻接表表示时,查找所有顶点的邻接点所需时间为O(E),访问顶点所需时间为O(V),故总的时间复杂度为O(V+E)。
当以邻接矩阵表示时,查找每个顶点的邻接点所需时间为O(V),故总的时间复杂度为O(V*V)。
4.图的应用(最小生成树、最短路径、拓扑排序、关键路径)
1)最小生成树
Prim算法、Kruskal算法
2)最短路径
Dijkstra算法、Floyd算法
3)拓扑排序
4)关键路径