n<=100000个字符的小写字母串,问用前m<=26个小写字母能拼出多少个和原串lcs=n-1的字符串。
首先把字符串划分成若干个连续相同的段,如aaa|bb|c|dd,然后题目即要求从里面挖掉一个再丢回去一个。如挖掉a,那么就剩aa|bb|c|dd,可以发现一个连续相同段挖谁都一样所以一个连续相同段只算一次,然后补一个。可以发现在自己的相同段中不能丢一个和原来一样的,而在其他地方同一个字母前后丢一样的会算重,如aab b bcdd,和aabb b cdd,也就是在第二个b前后丢b效果相同,所以每个地方只能放m-1个字符,就加上n*(m-1)。
然而还会算重。。比如ababab这样的连续段,任意挖一个补到后面一定对应一个后面补到前面的方案,比如这里把第一个a补到最后变成bababa,和把最后一个b提到最前是一样的。假设有一段连续的abab……串长度len,那么他有len*(len-1)/2个abab……的子串,就减掉即可。

1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 #include<algorithm> 5 //#include<iostream> 6 using namespace std; 7 8 int n,m; 9 #define maxn 200011 10 char s[maxn]; 11 12 int main() 13 { 14 scanf("%d%d",&n,&m); 15 scanf("%s",s+1); 16 #define LL long long 17 LL ans=n*(m-1); 18 for (int i=2;i<=n;i++) if (s[i]!=s[i-1]) ans+=n*(m-1); 19 int len=1; 20 for (int i=2;i<=n;i++) 21 { 22 if (len==1) if (s[i-1]!=s[i]) len++;else{} 23 else if (s[i-2]==s[i]) len++; 24 else 25 { 26 ans-=1ll*len*(len-1)/2; 27 if (s[i]==s[i-1]) len=1; 28 else len=2; 29 } 30 } 31 ans-=1ll*len*(len-1)/2; 32 printf("%lld ",ans); 33 return 0; 34 }
YYL的做法: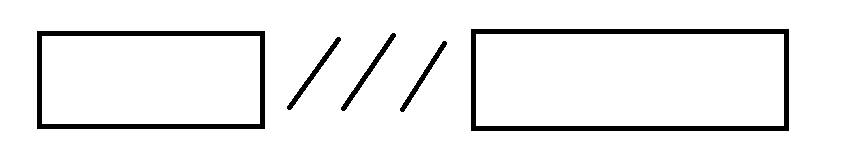
关注这种匹配方式的开始条件和结尾条件,即每个位置作为斜线区域开始的方案数,作为终止区域结束的方案数。需要分个类:
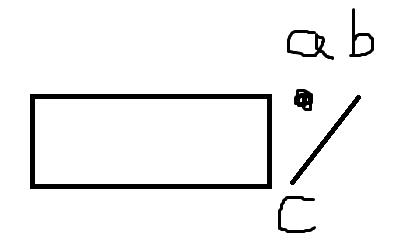
这里a!=b会有1的开始位置贡献。

这里若a=b,d会有m-1种结束方式;若a!=b,d会有m-2种结束方式。
待填坑。
