n<=10000局剪刀石头布,对面第i局出Ai,m<=10000种对你出什么提出的要求:Xi Yi Wi 表示第Xi局和第Yi局,Wi=1:必须不同;Wi=0:必须相同,问是否存在你一局都不能输的可行解。
一开始对面就把你每局的选择减成2个了,又是一个2-SAT问题。至于建图一定要考虑周全!注意一个条件对Xi和Yi带来的影响都要考虑!
A和B必须不同:
A和B必须相同: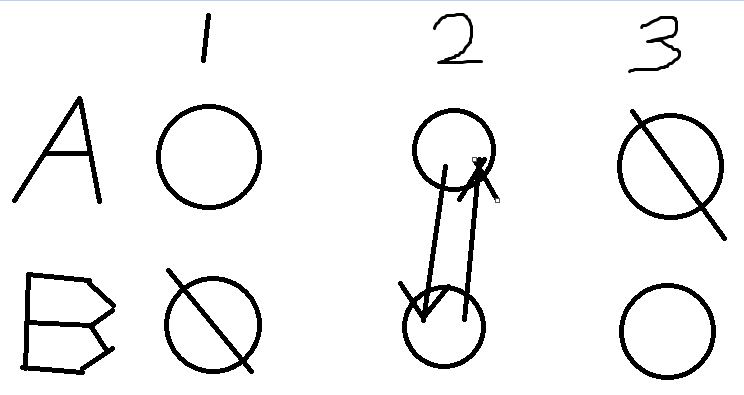 错误!未考虑清楚“必须相同”的含义,就是说,如果B没有一样的,那么A这个就不能选!
错误!未考虑清楚“必须相同”的含义,就是说,如果B没有一样的,那么A这个就不能选!
那么还要把这些不能选的点删掉吗?看了大神博客,发现神奇姿势: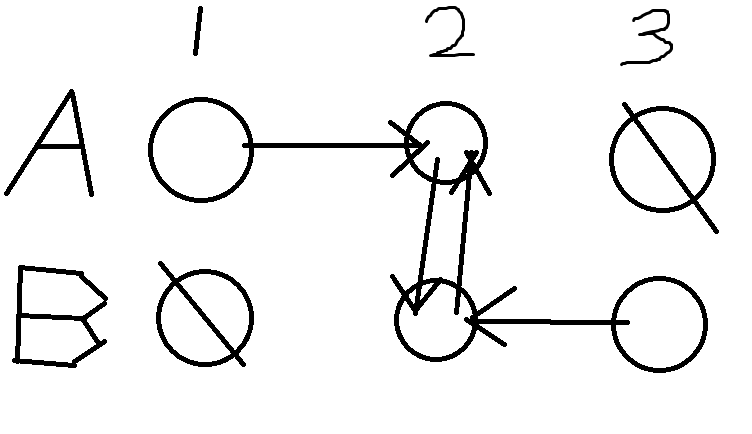 这样A1和B3就永远不可能选了,因为一旦选立刻出现矛盾。
这样A1和B3就永远不可能选了,因为一旦选立刻出现矛盾。
注意事项:由于建边过程繁琐,中途思路混乱WA了一次。注意检查!!!

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<cstdlib> 5 #include<cmath> 6 //#include<iostream> 7 using namespace std; 8 9 int n,m,T; 10 #define maxn 10011*2 11 #define maxe 10011*4 12 struct Edge{int to,next;}; 13 struct Graph 14 { 15 Edge edge[maxe];int le; 16 int first[maxn],vis[maxn]; 17 void clear() 18 { 19 le=2; 20 memset(first,0,sizeof(first)); 21 } 22 void insert(int x,int y) 23 { 24 edge[le].to=y; 25 edge[le].next=first[x]; 26 first[x]=le++; 27 } 28 int sta[maxn],top; 29 bool dfs(int x) 30 { 31 if (vis[x^1]) return 0; 32 if (vis[x]) return 1; 33 vis[x]=1; 34 sta[++top]=x; 35 for (int i=first[x];i;i=edge[i].next) 36 if (!dfs(edge[i].to)) return 0; 37 return 1; 38 } 39 bool twosat() 40 { 41 memset(vis,0,sizeof(vis)); 42 for (int i=1;i<=n;i++) 43 if (!vis[i*2] && !vis[i*2+1]) 44 { 45 top=0; 46 if (!dfs(i*2)) 47 { 48 for (;top;top--) vis[sta[top]]=0; 49 if (!dfs(i*2+1)) return 0; 50 } 51 } 52 return 1; 53 } 54 }G; 55 struct Point 56 { 57 int a,b; 58 }game[maxn]; 59 int x,y,w; 60 int main() 61 { 62 scanf("%d",&T); 63 for (int t=1;t<=T;t++) 64 { 65 scanf("%d%d",&n,&m); 66 for (int i=1;i<=n;i++) 67 { 68 scanf("%d",&x); 69 if (x==1) {game[i].a=1;game[i].b=2;} 70 if (x==2) {game[i].a=2;game[i].b=3;} 71 if (x==3) {game[i].a=1;game[i].b=3;} 72 } 73 G.clear(); 74 for (int i=1;i<=m;i++) 75 { 76 scanf("%d%d%d",&x,&y,&w); 77 if (w) 78 { 79 if (game[x].a==game[y].a) 80 { 81 G.insert(x*2,y*2+1); 82 G.insert(y*2,x*2+1); 83 } 84 if (game[x].a==game[y].b) 85 { 86 G.insert(x*2,y*2); 87 G.insert(y*2+1,x*2+1); 88 } 89 if (game[x].b==game[y].a) 90 { 91 G.insert(x*2+1,y*2+1); 92 G.insert(y*2,x*2); 93 } 94 if (game[x].b==game[y].b) 95 { 96 G.insert(x*2+1,y*2); 97 G.insert(y*2+1,x*2); 98 } 99 } 100 else 101 { 102 if (game[x].a==game[y].a) 103 { 104 G.insert(x*2,y*2); 105 G.insert(y*2,x*2); 106 } 107 else if (game[x].a==game[y].b) 108 { 109 G.insert(x*2,y*2+1); 110 G.insert(y*2+1,x*2); 111 } 112 else G.insert(x*2,x*2+1); 113 if (game[x].b==game[y].a) 114 { 115 G.insert(x*2+1,y*2); 116 G.insert(y*2,x*2+1); 117 } 118 else if (game[x].b==game[y].b) 119 { 120 G.insert(x*2+1,y*2+1); 121 G.insert(y*2+1,x*2+1); 122 } 123 else G.insert(x*2+1,x*2); 124 if (game[y].a!=game[x].a && game[y].a!=game[x].b) 125 G.insert(y*2,y*2+1); 126 if (game[y].b!=game[x].a && game[y].b!=game[x].b) 127 G.insert(y*2+1,y*2); 128 } 129 } 130 printf("Case #%d: ",t); 131 if (G.twosat()) printf("yes");else printf("no"); 132 puts(""); 133 } 134 return 0; 135 }
