题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1588
题目大意:g(i)= k * i + b. 给定 k 和 b,求0 <= i < n 的斐波那契数 F(g(i))的和模1,000,000,000.
解题思路:
矩阵快速幂再加上二分矩阵公式。
首先,我们需要认识到的一点是:对于这种求斐波那契数的题,很多都是用矩阵快速幂根据如下公式来计算的。
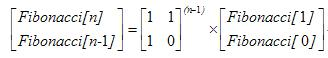
我们在此把中间那个01矩阵设为A。要求 The_Sum_of_F(g(i)),只需求出 A^(g(0)-1) + A^(g(1)-1) + A^(g(2)-1) + ... + A^(g(n-1)-1) = A^(b-1) + A^(i+b-1) + A^(2*i+b-1) + ...... = A^(b-1) + A^(b-1) * (A^i + A^(2*i) + A^(3*i) + ......). A^(b-1) = Ab, A^i = Ai,这些都可以用矩阵快速幂求出来。那么式子就变成:Ab+Ab * (Ai + Ai^2 + Ai^3 + ......).加粗的那部分用二分矩阵公式递归求出。下面给出二分矩阵公式的一个例子:A^1+A^2+A^3+A^4+A^5+A^6=(A^1+A^2+A^3)+A^3(A^1+A^2+A^3)。
AC代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 typedef long long ll; 6 const int maxn = 1000; 7 struct Matrix { 8 ll mat[4][4]; 9 }; 10 Matrix E; 11 ll M; 12 Matrix Multiply(Matrix x,Matrix y) { 13 Matrix temp; 14 memset(temp.mat, 0, sizeof(temp.mat)); 15 for (int i = 0; i < 2; i++) 16 for (int j = 0; j < 2; j++) { 17 for (int k = 0; k < 2; k++) { 18 temp.mat[i][j] += (x.mat[i][k] * y.mat[k][j]%M); 19 temp.mat[i][j]%=M; 20 } 21 } 22 return temp; 23 } 24 Matrix Add(Matrix x,Matrix y){ 25 Matrix temp; 26 for (int i = 0; i < 2; i++){ 27 for (int j = 0; j < 2; j++) { 28 temp.mat[i][j]=(x.mat[i][j]+y.mat[i][j])%M; 29 } 30 } 31 return temp; 32 } 33 Matrix Fast_Power(Matrix a, int m) { //求a的m次幂 34 Matrix res; 35 memset(res.mat, 0, sizeof(res.mat)); 36 for (int i = 0; i < 2; i++) res.mat[i][i] = 1; 37 while (m) { 38 if (m & 1) res = Multiply(res, a); 39 m >>= 1; 40 a = Multiply(a, a); 41 } 42 return res; 43 } 44 Matrix Binary_add(Matrix B,int t){ 45 if(t==1) return B; 46 if(t%2==1){ 47 return Add(Multiply(Binary_add(B,(t-1)/2),Add(E,Fast_Power(B,(t-1)/2))),Fast_Power(B,t)); 48 } 49 else 50 return Multiply(Binary_add(B,t/2),Add(E,Fast_Power(B,t/2))); 51 } 52 int main() 53 { 54 E.mat[0][0]=E.mat[1][1]=1; 55 E.mat[0][1]=E.mat[1][0]=0; 56 Matrix A; 57 A.mat[0][0]=A.mat[0][1]=A.mat[1][0]=1; 58 A.mat[1][1]=0; 59 ll k,b,n,t; 60 while(scanf("%lld%lld%lld%lld",&k,&b,&n,&M)==4){ 61 Matrix Ab,B,ans; 62 B=Fast_Power(A,k); 63 Ab=Fast_Power(A,b); 64 ans=Add(Ab,Multiply(Ab,Binary_add(B,n-1))); 65 printf("%lld ",ans.mat[1][0]); 66 } 67 return 0; 68 }