论文解读（Graph Barlow Twins）《Graph Barlow Twins: A selfsupervised representation learning framework for graphs》

论文信息

论文标题：Graph Barlow Twins: A self-supervised representation learning framework for graphs
论文作者：Piotr Bielaka, Tomasz Kajdanowicza, Nitesh V. Chawlab
论文来源：2022,arXiv
论文地址：download 
论文代码：download 

1 Abstract

　　针对的问题依然是：对比学习需要负采样。

　　本文的解决方法：Graph Barlow Twins，利用一个基于互相关的损失函数，而不是负样本。

2 Introduction

　　最近的对比学习流行无负采样的策略，一些相关典型的工作：BYOL [6]、SimSiam [3]、Barlow Twins [28] 。这些模型使用 siamese network architectures 并采用一些  asymmetry 、batch and layer normalizations 去防止崩塌到平凡解。【此处我不能理解，为何有此一说】

3 Proposed framework

　　整体框架如下：

　　

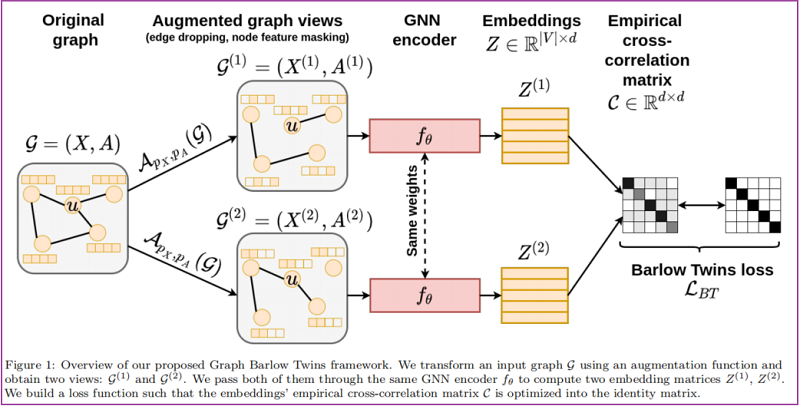
3.1 Generating graph views via augmentation

　　通过数据增强 edge dropping 和 node feature masking 分别生成 两个增强图 $\mathcal{G}^{(1)}$ 、$\mathcal{G}^{(2)}$ 。

• • 对于 edge dropping 根据 $\mathcal{B}\left(1-p_{A}\right)$ mask 大小为 $|\mathcal{E}|$ 的边；
  • 对于 node feature masking 根据 $\mathcal{B}\left(1-p_{X}\right)$ mask 大小为 $k$ 的节点；　

3.2 Encoder network

　　本文使用过 GCN、GAT 作为 Encoder  $f_{\theta}: \mathcal{G} \rightarrow \mathbb{R}^{|\mathcal{V}| \times d}$，

3.3 Loss function

　　首先，对 Encoder 生成的嵌入  $Z^{(1)}$、$Z^{(2)}$ 进行标准化（normalize），然后计算经验互相关矩阵 $\mathcal{C} \in \mathbb{R}^{d \times d}$：

　　　　${\large \mathcal{C}_{i j}=\frac{\sum\limits_{b} Z_{b, i}^{(1)} Z_{b, j}^{(2)}}{\sqrt{\sum\limits _{b}\left(Z_{b, i}^{(1)}\right)^{2}} \sqrt{\sum\limits_{b}\left(Z_{b, j}^{(2)}\right)^{2}}}} $

　　其中，$b$ 代表的是 batch index 。

　　上述 cross-correlation matrix $\mathcal{C}$ 通过 Barlow Twins loss function $\mathcal{L}_{\mathrm{BT}}$ 进行优化：

　　　　$\mathcal{L}_{\mathrm{BT}}=\sum\limits _{i}\left(1-\mathcal{C}_{i i}\right)^{2}+\lambda \sum\limits_{i} \sum\limits_{j \neq i} \mathcal{C}_{i j}{ }^{2}$

　　其中，$\lambda\gt 0$ 代表权衡参数，原作者设置为 $\frac{1}{d}$ ，但是我们也可以自己通过超参数调优设置。

　　公式含义：要求 节点 $i$ 自身的互相关性趋于 $1$，对于节点 $i$ 和 节点 $j \ne i$ 之间的互相关性趋于 $0$。

4 Experiments

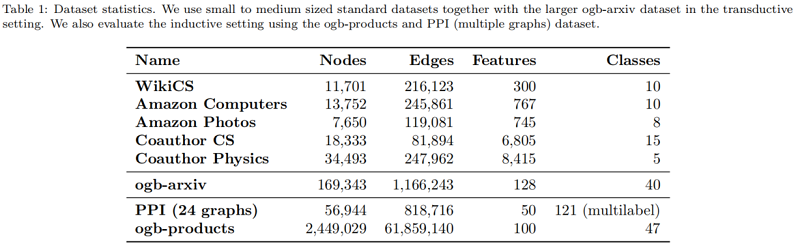
数据集

　　

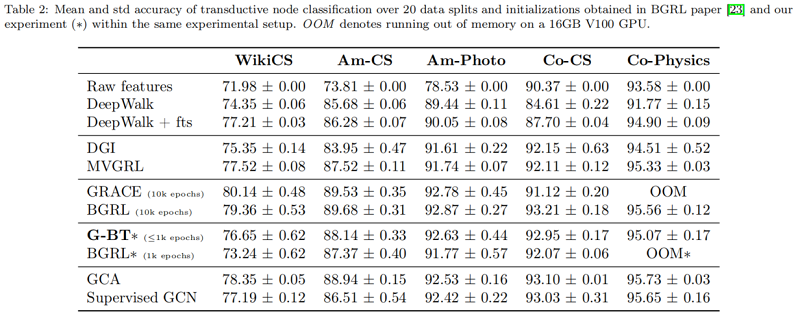
节点分类

　　

实验细节

　　对于超参数，和Encoder 的设计得自己去看代码，本文超参数基本上是通过网格搜索获得的，Encoder 也没有和基准设置一样。

5 Conclusions

　　使用互相关矩阵实现节点一致性原则。

扯皮

　　改论文 1 年前我就看过了，今天只不过以博客形式记录一下，毕竟还是有点东西可以学习的，但是该论文质量显然达不到当前水平。

　　[19] 这篇文献是1990 年的，第一次提出了自监督的概念。