论文信息
论文标题:Predict then Propagate: Graph Neural Networks meet Personalized PageRank
论文作者:Johannes Gasteiger, Aleksandar Bojchevski, Stephan Günnemann
论文来源:2019,ICLR
论文地址:download
论文代码:download
1-Abstract
本文主要将 PageRank 算法引入到 GNNs ,提出了 PPNP 模型 和APPNP 模型。
2-Introduction
问题:
-
- 增大邻域范围,充分利用领域信息;【传播多层——消息传递机制的本质,也可以看做随机游走】
- 解决过平滑问题(一般均为传播多层造成的过平滑);
受 带重启随机游走(random walk)的影响,本文利用 personalized PageRank 代替随机游走 ,来增加传送到根节点的机会,以避免过平滑现象(主要是更多的考虑根节点的邻域),此外该模型允许使用更多的传播层数。【通过 $\text{Eq.4}$ 便于理解】
3 Graph convolutional networks and their limited range
半监督节点分类 GCN:
$\boldsymbol{Z}_{\mathrm{GCN}}=\operatorname{softmax}\left(\hat{\tilde{\tilde{A}}} \operatorname{ReLU}\left(\hat{\tilde{\tilde{A}}} \boldsymbol{X} \boldsymbol{W}_{0}\right) \boldsymbol{W}_{1}\right) \quad\quad\quad(1)$
其中,$\hat{\tilde{\boldsymbol{A}}}=\tilde{\boldsymbol{D}}^{-1 / 2} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-1 / 2}$。
存在的问题:【APPNP 所解决的问题 】
-
- 不能使用更多的传播层,因为会造成过平滑;
- 层数增加,参数量增加;
4 Personalized propagation of neural predictions
早起版本 PageRank:
$\pi_{\mathrm{pr}}=A_{\mathrm{rw}} \pi_{\mathrm{pr}}, \quad\quad\text { with }\quad\quad A_{\mathrm{rw}}=A D^{-1}$
以及考虑根节点信息,提出 personalized PageRank 算法:【类似带重启的随机游走,缓解过平滑】
其中:
-
- $\hat{\tilde{A}}=\tilde{\boldsymbol{D}}^{-1 / 2} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-1 / 2}$;
- $i_x$ 表示初始根节点的特征;
计算得到平稳状态后的分布:
用单位矩阵代替指标向量 $i_x$ 得 personalized PageRank matrix:
$\mathbf{\Pi}_{\mathrm{ppr}}=\alpha\left(\boldsymbol{I}_{n}-(1-\alpha) \hat{\tilde{ A }}\right)^{-1}$
$\mathbf{\Pi}_{\mathrm{ppr}}$ 中的元素 $yx$ 可以理解为 节点 $x$ 对节点 $y$ 的影响分数 $I(x, y) \propto \Pi_{\mathrm{ppr}}^{(y x)}$。【其实就是 节点 $x$ 转移到节点 $y$ 的概率值】
Note:上述式子可逆的时候需要满足 $\frac{1}{1-\alpha}>1$ 且不能为 $\hat{\tilde{A}}$ 的特征值。
借由上述阐述,得到 PPNP 模型:
$\boldsymbol{Z}_{\mathrm{PPNP}}=\operatorname{softmax}\left(\alpha\left(\boldsymbol{I}_{n}-(1-\alpha) \hat{\tilde{ A }}\right)^{-1} \boldsymbol{H}\right), \quad \boldsymbol{H}_{i,:}=f_{\theta}\left(\boldsymbol{X}_{i,:}\right)\quad\quad\quad(3)$
Note:直接计算 $\Pi_{\mathrm{ppr}}$ ,具有高计算复杂度且需要 $\mathcal{O}\left(n^{2}\right)$ 的内存空间。【APPNP 改进的地方】
APPNP 通过幂次迭代逼近 topic-sensitive PageRank 来实现线性计算复杂度。传播过程为:
$\begin{array}{l}\boldsymbol{Z}^{(0)} &=&\boldsymbol{H}=f_{\theta}(\boldsymbol{X}) \\\boldsymbol{Z}^{(k+1)} &=&(1-\alpha) \hat{\tilde{A}} \boldsymbol{Z}^{(k)}+\alpha \boldsymbol{H} \\\boldsymbol{Z}^{(K)} &=&\operatorname{softmax}\left((1-\alpha) \hat{\tilde{\boldsymbol{A}}} \boldsymbol{Z}^{(K-1)}+\alpha \boldsymbol{H}\right)\end{array}\quad\quad\quad(4)$
这个迭代方案的收敛性证明如下:

在 PPNP 和 APPNP 中,影响每个节点的邻域的大小都可以通过传送概率 $\alpha $ 进行调整。
附:图扩散
$\mathcal{T}_{\mathbf{A}}(\mathbf{A})=\sum_{k=0}^{\infty} \Theta_{k} \mathbf{S}^{k}$
其中:
- $\mathbf{S} \in \mathbb{R}^{N \times N}$ 是广泛的转移矩阵
- $\Theta$ 是加权系数,且 $\sum_{k=0}^{\infty} \Theta_{k}=1 , \Theta_{k} \in[0,1]$
Personalized PageRank (PPR) kernal
其中:
- $\mathbf{S}=\mathbf{D}^{-1 / 2} \mathbf{A D}^{-1 / 2}$
- $\Theta_{k}=\alpha(1-\alpha)^{k}$
得:
- $\mathcal{T}_{\mathbf{A}}^{P P R}(\mathbf{A})=\alpha\left(\mathbf{I}_{n}-(1-\alpha) \mathbf{D}^{-1 / 2} \mathbf{A} \mathbf{D}^{-1 / 2}\right)^{-1}$
5 Experimental setup
消息传递算法对 数据划分 和 权重初始化 都非常敏感。

不同模型在随机数据划分 和 随机权重初始化的标准差
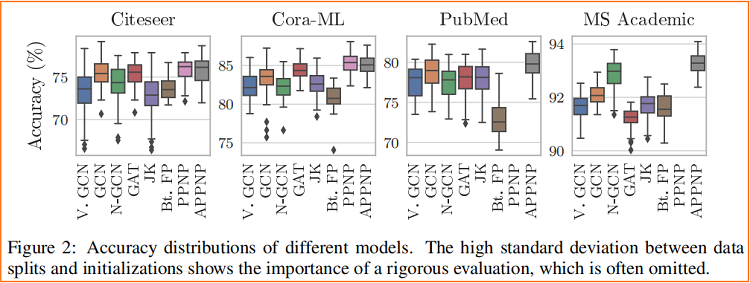

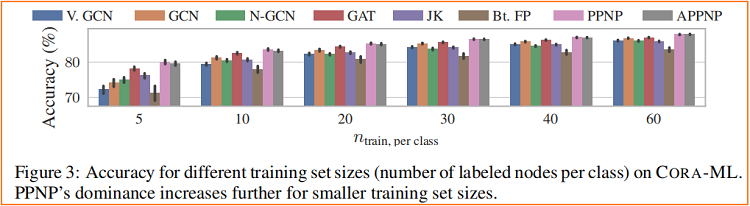
6 Conclusion
在本文中,我们介绍了神经预测(PPNP)及其快速近似APPNP。我们通过考虑GCN和PageRank之间的关系并将其扩展到个性化PageRank来导这个模型。这个简单的模型解耦了预测和传播,并解决了许多消息传递模型中固有的有限范围的问题,而没有引入任何额外的参数。它使用来自一个大的、可调节的(通过传送概率 $\alpha$)邻域的信息来对每个节点进行分类。该模型在计算上高效,优于目前最先进的研究,在多个图上的半监督分类方法。