1 前言
蒙特卡罗法有 直接抽样法、接收-拒绝抽样法、重要性抽样法。
2 直接抽样法
假如 $p(x)$ 是要采样的分布。若可以得到 $x$ 的概率密度函数 $p(x)$, 对 $p(x)$ 求积分得到累积分布函数 $F(x)$,显然 $x$ 和 $y$ 是一 一对应的。
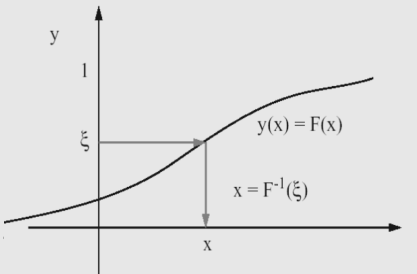
先随机抽取 $y$,然后通过求 $F(x)$ 的反函数 $F^{-1}(y)$ 得到随机变量 $x$ 的值:
$\boldsymbol{x}=\boldsymbol{F}^{-1}(\boldsymbol{y})$
随机变量 $y $ 在区间 $[0,1]$ 上均匀分布 $\Rightarrow$ 利用 $[0,1]$ 区 间上均匀分布随机数产生器抽取。
同理可以抽样出 $\mathrm{N}$ 个样本点 $x^{(1)},x^{(2)}, \ldots, x^{(N)}$
该方法的缺点是现实中很难得到概率密度函数,因此累积分布函数是求不出来的,所以很难通过这种方法去抽样得到样本点。这种方法只能适用于一 些非常有限的分布。
3 接收-拒绝抽样法
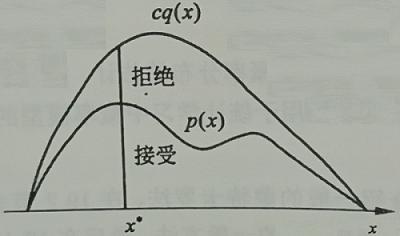
其中,$p(x)$ 是概率密度函数,$q(x)$ 为建议分布函数,$c$ 为 $q(x)$ 前的参数。
由于概率密度累积和为 $1$ ,故建议分布 $q(x)$ 不可能处处大于 $p(x)$ ,因此在 $q(x)$ 前面乘上一个参数 $c$,使其位于 $p(x)$ 之上,使其满足 $\forall x_{i}, c q\left(x_{i}\right) \geq p\left(x_{i}\right)$ 如图所示。
引入建议分布 $q(x)$ 的原因是在现实中 $p(x)$ 往往比较复杂,我们无法直接从 $p(x)$ 中采样。而 $q(x)$ 是相对比较简单的分布我们可以直接从里面采样, 再看看抽样的样本点是否能够代表 $p(x)$ 。
具体步骤如下:
输入:抽样的目标概率分布的概率密度函数 $p(x)$;
输出:概率分布的随机样本 $x_{1} \cdot x_{2}, \ldots, x_{n} $;
参数:样本数 $n$;(1) 选择合适的概率密度函数作为建议分布 $q(x)$,使其对任 $x$ 满足 $c q(x) \geq p(x)$ ,其中 $c>0$;
(2) 在建议分布 $q(x)$ 随机抽样得到样本 $x^{*}$ ,再按照均匀分布在 $(0,1)$ 范围内抽样得到 $u$;
(3) 如果 $u \leq \frac{p\left(x^{*}\right)}{c q\left(x^{*}\right)}$ ,则将 $x^{*}$ 作为抽样结果;否则,回到步骤 (2);
(4) 直至得到 $\mathrm{n}$ 个随机样本,结束。
解释一下这里 $\mathrm{u}$ 的用处。当 $p(x)$ 和 $c q(x)$ 接近时,也就是图中拒绝域比较窄时, $\frac{p\left(x^{*}\right)}{c q\left(x^{*}\right)}$ 比例接近 $1$,这时 $\mathrm{u}$ 在 $(0,1)$ 中取值满足小于 $\frac{p\left(x^{*}\right)}{c q\left(x^{*}\right)}$ 的概率比较大,接受率高,抽样效率比较高; 而当 $\frac{p\left(x^{*}\right)}{c q\left(x^{*}\right)}$ 比较小时,就会导致拒绝比例比较高,抽样效率较低。这样做能达到在 $p(x)$ 和 $c q(x)$ 接近的地方多抽样,在差异大的地方少抽样的效果。
接受-拒绝法的优点是容易实现,缺点是效率可能不高。如果 $p(x)$ 的涵盖体积占 $c q(x)$ 的涵盖体积的比例很低,就会导致拒绝的比例很高,抽样效率很低。注意,一般是在高维空间进行抽样,即使 $p(x)$ 与 $c q(x)$ 很接近,两者涵盖体积的差异也可能很大(与我们在三维空间 的直观不同)。
例子:
假设要抽样的分布 $p(x)$ 是:
$p(x)=\frac{1}{1.2113}\left(0.3 \exp \left(-(z-0.3)^{2}\right)+0.7 \exp \left(-(z-2)^{2} / 0.3\right)\right.$
在这个例子中,选择均值为 $1.4$,方差为 $1.2$ 的正态分布作为我们的建议分布,取常数 $C =2.5$。
代码片段:
from scipy.stats import norm
import seaborn
import numpy as np
seaborn.set()
import matplotlib.pyplot as plt
# 目标采样分布的概率密度函数
def p(x):
return (0.3 * np.exp(-(x - 0.3) ** 2) + 0.7 * np.exp(-(x - 2.) ** 2 / 0.3)) / 1.2113
# 建议分布G
norm_rv = norm(loc=1.4, scale=1.2)
# C值
C = 2.5
x = np.arange(-4., 6., 0.01)
plt.plot(x, p(x), color='r', lw=5, label='p(x)')
plt.plot(x, C*norm_rv.pdf(x), color='b', lw=5, label='C*g(x)')
plt.legend()
plt.show()
输出结果:

接下来具体使用接受-拒绝算法
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform, norm
import seaborn
seaborn.set()
# 目标采样分布的概率密度函数
def p(x):
return (0.3 * np.exp(-(x - 0.3) ** 2) + 0.7 * np.exp(-(x - 2.) ** 2 / 0.3)) / 1.2113
# 建议分布
norm_rv = norm(loc=1.4, scale=1.2)
# C值
C = 2.5
uniform_rv = uniform(loc=0, scale=1)
sample = []
for i in range(100000):
Y = norm_rv.rvs(1)[0]
U = uniform_rv.rvs(1)[0]
if p(Y) >= U * C * norm_rv.pdf(Y):
sample.append(Y)
x = np.arange(-3., 5., 0.01)
plt.gca().axes.set_xlim(-3, 5)
plt.plot(x, p(x), color='r')
plt.hist(sample, color='b', bins=150, normed=True, edgecolor='k')
plt.show()
输出结果:

我们通过接受-拒绝采样方法,进行了10万次的数据采样,最后把采样结果绘制成。通过运行结果我们发现,柱状图的形状几乎和原始目标分布的概率密度函数曲线完全拟合。由此通过实践证明了这个采样的方法确实是有效的,他高度近似的拟合了原始样本的分布特性。
3 重要性抽样法
上面两种采样方法或多或少都有一些问题。
上面描述了两种从另一个分布获取指定分布的采样样本的算法,对于1. 在实际工作中,一般来说我们需要采样的分布都及其复杂, 太可能求解出它的反函数,但 $p(x)$ 的值也许还是可以计算的。对于 2 .找到一个合适的 $c q(x)$ 往往很困难,接受概率有可能会很低。 那我们回过头来看我们采样的目的: 其实是想求得 $E[f(x)]$, $x \sim p$ , 也就是
$E[f(x)]=\int_{x} f(x) p(x) d x$
如果符合 $\mathrm{p}(\mathrm{x})$ 分布的样本不太好生成,我们可以引入另一个分布 $q(x)$ ,可以很方便地生成样本。使得
$\begin{aligned}\int_{x} f(x) p(x) d x &=\int_{x} f(x) \frac{p(x)}{q(x)} q(x) d x \\&=\int_{x} g(x) q(x) d x\end{aligned}$
其中,$g(x)=f(x) \frac{p(x)}{q(x)}=f(x) w(x) $
我们将问题转化为了求 $g(x)$ 在 $q(x)$ 分布下的期望! ! !
我们称其中的 $w(x)=\frac{p(x)}{q(x)}$ 叫做Importance Weight.
重要性抽样法解决的问题:
首先当然是我们本来没办法直接从 $p$ 进行采样,这个是我们看到的,重要性采样将之转化为了从 $q$ 分布进行采样;同时重要性采样有时候还可以改进原来的采样,比如说:
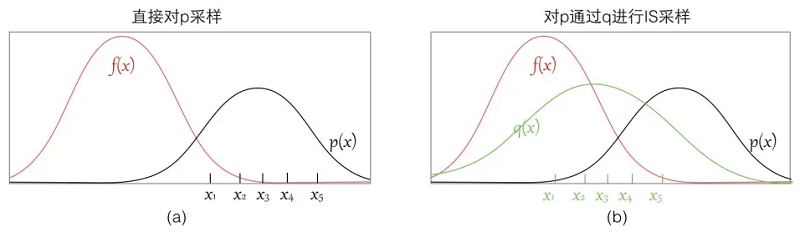
可以看到如果我们直接从 $p$ 进行采样,而实际上这些样本对应的 $f(x)$ 都很小,采样数量有限的情况下很有可能都无法获得 $f(x)$ 值较大的样 本,这样评估出来的期望偏差会较大;
而如果我们找到一个 $q$ 分布,使得它能在 $f(x) * p(x)$ 较大的地方采集到样本,则能更好地逼近 $[E f(x)]$ ,因为有Importance Weight控制其比重,所以也不会导致结果出现过大偏差。
所以选择一个好的q也能帮助你sample出来的效率更高,要使得 $f(x) p(x)$ 较大的地方能被sample出来。
https://www.bilibili.com/read/cv4939412
https://blog.csdn.net/lukas_ten/article/details/114458591