论文信息
论文标题:Graph infoclust: Leveraging cluster-level node information for unsupervised graph representation learning
论文作者:Costas Mavromatis, G. Karypis
论文来源:2021, PAKDD
论文地址:download
论文代码:download
1 Introduction
创新点:
-
- 使用聚类级对比损失;
- 使用了 $\text{ClusterNet}$ 聚类算法;
2 Method
想法:基于互信息最大化
-
- node (fine-grain) representations and the global graph summary
- node (fine-grain) representations and corresponding cluster (coarse-grain) summaries
2.1 Overview of GIC
整体框架:
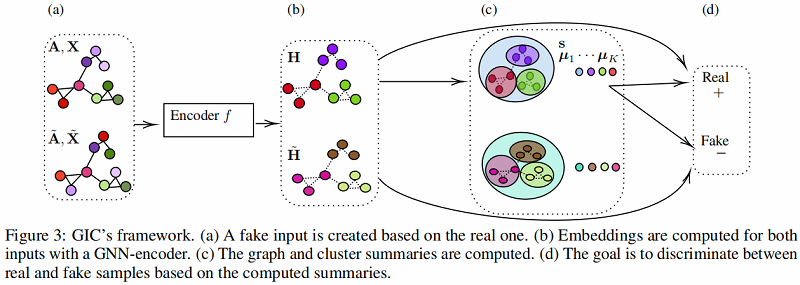
2.2 Implementation Details
-
- $\tilde{\mathbf{A}}:=\mathbf{A}$
- $\tilde{\mathbf{X}}:=\operatorname{shuffle}\left(\left[\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{N}\right]\right)$
嵌入矩阵:
$\mathbf{H}=f_{G N N}(\mathbf{A}, \mathbf{X})$
$\tilde{\mathbf{H}}=f_{G N N}(\tilde{\mathbf{A}}, \tilde{\mathbf{X}})$
其中 $f_{\mathrm{GNN}}$ 是一层的 $\text{GCN}$:
$\mathbf{H}^{(l+1)}=\sigma\left(\hat{\mathbf{D}}^{-\frac{1}{2}} \hat{\mathbf{A}} \hat{\mathbf{D}}^{-\frac{1}{2}} \mathbf{H}^{(l)} \boldsymbol{\Theta}\right)$
图级表示 $\mathbf{s} \in \mathbb{R}^{1 \times F^{\prime}}$:
$\mathbf{s}=\sigma\left(\frac{1}{N} \sum\limits _{i=1}^{N} \mathbf{h}_{i}\right) \quad\quad\quad(4)$
使用类似 $K-Means$ 的聚类算法 $\text{ClusterNet}$ 获得聚类质心 $\boldsymbol{\mu}_{k} \in \mathbb{R}^{1 \times F^{\prime}}$ ,通过下列式子迭代设置、更新聚类质心:
${\large \boldsymbol{\mu}_{k}=\frac{\sum\limits _{i} r_{i k} \mathbf{h}_{i}}{\sum\limits_{i} r_{i k}}} \quad k=1, \ldots, K\quad\quad\quad(6)$
${\large r_{i k}=\frac{\exp \left(-\beta \operatorname{sim}\left(\mathbf{h}_{i}, \boldsymbol{\mu}_{k}\right)\right)}{\sum_{k} \exp \left(-\beta \operatorname{sim}\left(\mathbf{h}_{i}, \boldsymbol{\mu}_{k}\right)\right)} \quad k=1, \ldots, K} \quad\quad\quad(7)$
根据 $\text{Eq.6}$ 获得聚类级表示 $\mathbf{z}_{i} \in \mathbb{R}^{1 \times F^{\prime}}$:
$\mathbf{z}_{i}=\sigma\left(\sum\limits _{k=1}^{K} r_{i k} \boldsymbol{\mu}_{k}\right)\quad\quad\quad(5)$
总损失函数:
$\mathcal{L}=\alpha \mathcal{L}_{1}+(1-\alpha) \mathcal{L}_{K}\quad\quad\quad(3)$
其中:
$\begin{aligned}\mathcal{L}_{1} &=\sum\limits _{i=1}^{N} \mathbb{E}_{(\mathbf{X}, \mathbf{A})}\left[\log \mathcal{D}_{1}\left(\mathbf{h}_{i}, \mathbf{s}\right)\right] +\sum\limits_{i=1}^{N} \mathbb{E}_{(\tilde{\mathbf{X}}, \tilde{\mathbf{A}})}\left[\log \left(1-\mathcal{D}_{1}\left(\tilde{\mathbf{h}}_{i}, \mathbf{s}\right)\right)\right]\end{aligned}\quad\quad\quad(1)$
$\begin{aligned}\mathcal{L}_{K} &=\sum_{i=1}^{N} \mathbb{E}_{(\mathbf{X}, \mathbf{A})}\left[\log \mathcal{D}_{K}\left(\mathbf{h}_{i}, \mathbf{z}_{i}\right)\right] +\sum_{i=1}^{N} \mathbb{E}_{(\tilde{\mathbf{X}}, \tilde{\mathbf{A}})}\left[\log \left(1-\mathcal{D}_{K}\left(\tilde{\mathbf{h}}_{i}, \mathbf{z}_{i}\right)\right]\right.\end{aligned}\quad\quad\quad(2)$
$\mathcal{D}_{1}\left(\mathbf{h}_{i}, \mathbf{s}\right)=\sigma\left(\mathbf{h}_{i}^{T} \mathbf{W} \mathbf{s}\right)\quad\quad\quad(8)$ $\mathcal{D}_{1}: \mathbb{R}^{F^{\prime}} \times \mathbb{R}^{F^{\prime}} \rightarrow \mathbb{R}$
$\mathcal{D}_{K}\left(\mathbf{h}_{i}, \mathbf{z}_{i}\right)=\sigma\left(\mathbf{h}_{i}^{T} \mathbf{z}_{i}\right)\quad\quad\quad(9)$ $\mathcal{D}_{K}: \mathbb{R}^{F^{\prime}} \times \mathbb{R}^{F^{\prime}} \rightarrow \mathbb{R}$
3 Experiment
数据集

基线实验
节点分类:

链接预测:

聚类:
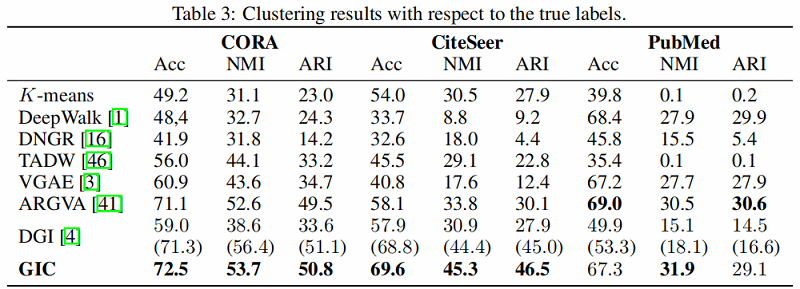
4 Conclusion
提出了Graph InfoClust(GIC),这是一种无监督的依赖于聚类级的图表示学习方法,它依赖于利用集群级的内容。GIC识别具有相似表示形式的节点,将它们聚类在一起,并最大化它们的互信息。这使得我们能够以更丰富的内容提高节点表示的质量,并在节点分类、链接预测、聚类和数据可视化等任务方面获得比现有方法更好的结果。