论文解读（S^3CL）《Structural and Semantic Contrastive Learning for Selfsupervised Node Representation Learning》 Learner

论文信息

论文标题：Structural and Semantic Contrastive Learning for Self-supervised Node Representation Learning
论文作者： Kaize Ding 、Yancheng Wang 、Yingzhen Yang、Huan Liu
论文来源：2022, arXiv
论文地址：download
论文代码：download

1 摘要

　　Graph Contrastive Learning (GCL) 研究方向：

• • encoding architecture
  • augmentation
  • contrastive objective

2 介绍

　　现存两阶段对比学习框架存在的问题：

• • Shallow Encoding Architecture　　
  • Arbitrary Augmentation Design　　
  • Semanticless Contrastive Objective　　

　　定义1：

• • 自监督节点表示学习: 给定一个属性图$\mathcal{G}=   (\mathbf{X}, \mathbf{A})$ ,目标是学习一个图编码器  $f_{\boldsymbol{\theta}}: \mathbb{R}^{N \times D} \times   \mathbb{R}^{N \times N} \rightarrow \mathbb{R}^{N \times D^{\prime}}$ ，不使用标签信息，这样生成的节点表示 $\mathbf{H} \in \mathbb{R}^{N \times D^{\prime}}=f_{\boldsymbol{\theta}}(\mathbf{X}, \mathbf{A})$ 可以用于不同的下游任务。

　　本文提出的方法： Simple Neural Networks with Structural and Semantic Contrastive Leanring（$S^3-CL$），包括三个部分：

• • An encoder network
  • A structural contrastive learning module
  • A semantic contrastive learning module

　　框架如下所示：

　　

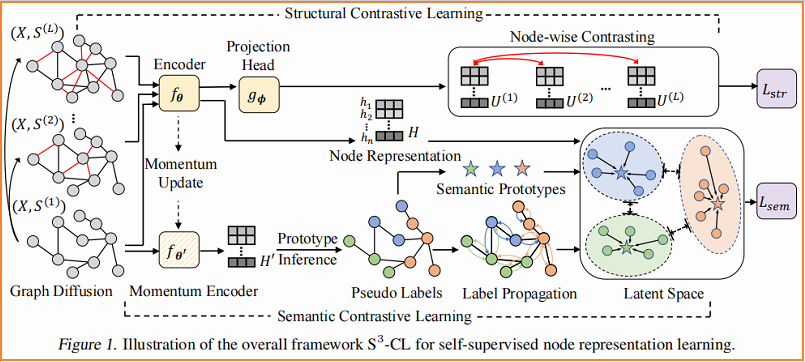
3 方法

3.1 Structural Contrastive Learning

　　在无监督表示学习中，对比学习方法将每个样本视为一个不同的类，旨在实现实例区分。以类似的方式，现有的GCL方法通过最大化不同增强视图中相同图元素的表示之间的一致性来实现节点级识别。

3.1.1 Structure Augmentation via Graph Diffusion

　　Step1 ：Graph Diffusion

 　　 Graph Diffusion ：

　　　　$\mathbf{S}=\sum\limits _{l=0}^{\infty} \theta_{l} \mathbf{T}^{l} \in \mathbb{R}^{N \times N}\quad\quad\quad(1)$

　　其中：

• • $\mathbf{T} \in \mathbb{R}^{N \times N}$ 是转移概率矩阵，$\mathbf{T} = \tilde{\mathbf{A}}_{s y m}=\tilde{\mathbf{D}}^{-1 / 2} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-1 / 2}$；　　
  • $\theta_{l}$ 是 $ l^{t h} -hop$ 邻居的权重参数，此处设置 $\theta_{l}=1 $，其他的权重参数设置为 $0$；　　

　　通过上述参数设置，那么：$\mathbf{S}^{(l)}=\tilde{\mathbf{A}}_{s y m}^{l}$ 。

　　Step2：Feature propagation

　　然后，使用增广图结构进行特征传播，并使用一层编码器网络 $f_{\boldsymbol{\theta}}(\cdot )$ 进一步计算节点表示，如下：

　　　　$\mathbf{H}^{(l)}=f_{\boldsymbol{\theta}}\left(\mathbf{S}^{(l)} \mathbf{X}\right)=\operatorname{ReLU}\left(\mathbf{S}^{(l)} \mathbf{X} \Theta\right)\quad\quad\quad(2)$

　　其中，$ \Theta \in \mathbb{R}^{N \times D^{\prime}}$ 代表着权重参数，计算出的节点表示 $\mathbf{H}^{(l)}$ 可以编码图中来自 $l-hops$ 邻域的特征信息。

　　为更好的利用局部-全局信息，本文进一步设置不同的 $\text{l}$ 来执行多个数据增强。具体来说，$\mathbf{H}^{(1)}$ 是从局部视图中学习的，因为只用了在直接邻居之间传递的信息，而 $\left\{\mathbf{H}^{(l)}\right\}_{l=2}^{L}$ 是从一组高阶视图中学习的，这些高阶视图编码了不同级别的全局结构信息。　　

　　本文的对比学习架构中，目标是通过最大化每个节点的互信息，最大化每个节点的局部视图和高阶视图之间的一致性。

　　这里并没有直接使用 $f_{\boldsymbol{\theta}}(\cdot )$ 输出的表示，而是进一步对生成的表示 $\mathbf{H}^{(l)}$ 使用一个投影头 $g_{\psi}(\cdot)$ 【一个两层MLP】，即生成 $\left\{\mathbf{U}^{(l)}\right\}_{l=1}^{L} $，其中 $ \mathbf{U}^{(l)}=g_{\psi}\left(\mathbf{H}^{(l)}\right)$。

3.1.2 Structural Contrastive Objective

　　最大化局部视图 $\mathbf{U}^{1}$ ，和高阶视图 $\mathrm{U}^{(l)}$ 之间的一致性（节点级）：

　　　　$\mathcal{L}_{s t r}^{(l)}=-\frac{1}{N} \sum\limits_{i=1}^{N} \log \frac{\exp \left(\mathbf{u}_{i}^{(1)} \cdot \mathbf{u}_{i}^{(l)} / \tau_{1}\right)}{\sum\limits_{j=0}^{M} \exp \left(\mathbf{u}_{i}^{(1)} \cdot \mathbf{u}_{j}^{(l)} / \tau_{1}\right)}\quad\quad\quad(3)$

　　其中：

• • $\mathbf{u}_{i}^{(1)}$  和  $\mathbf{u}_{i}^{(l)}$  分别代表着 $\mathbf{U}^{(1)}$ 和 $\mathbf{U}^{(l)}$ 的第 $i$ 行表示向量；
  • 定义$\left\{\mathbf{u}_{j}^{(l)}\right\}_{j=0}^{M}$ 拥有一个正样本，$M$ 个负样本；

　　所以总损失为：

　　　　$\mathcal{L}_{s t r}=\sum\limits _{l=2}^{L} \mathcal{L}_{s t r}^{(l)}\quad\quad\quad(4)$

　　最终的节点表示 $H$ 可以通过将 $\tilde{\mathbf{X}}=\frac{1}{L} \sum_{l=1}^{L} \mathbf{S}^{(l)} \mathbf{X}$ 输入编码器网络来计算，以保留局部和全局结构信息。

3.2 Semantic Contrastive Learning

　　为探讨输入图的语义信息，进一步提出了一个语义对比学习模块，该模块通过鼓励簇内紧凑性和簇间可分离性来明确地捕获数据语义结构。

　　它通过迭代的推断节点和其对应原型之间的聚类，并进行语义对比学习，促进节点在潜在空间中对应的聚类原型进行语义相似的聚类。Cluster 原型的表示用一个矩阵表示 $\mathbf{C} \in \mathbb{R}^{K \times D^{\prime}} $ ，这里的 $K$ 代表着原型数目。$\mathbf{c}_{k}$ 代表着 $\mathbf{C} $ 的第 $k$ 行，即第 $k$ 个原型的表示向量。节点 $v_i$ 的原型分配定义为 $\mathcal{Z}=\left\{z_{i}\right\}_{i=1}^{n}$，其中$z_{i} \in\{1, \ldots, K\} $ 。

3.2.1 Bayesian Non-parametric Prototype Inference.

　　我们的语义对比学习模块的一个关键组成部分是推断出具有高度代表性的 cluster prototypes。然而，在自监督节点表示学习的设置下，最优的聚类数量是未知的，因此很难直接采用 K-means 等聚类方法对节点进行聚类。为了解决这个问题，我们提出了一种贝叶斯非参数原型推理（  Bayesian non-parametric prototype inference）算法来近似最优的聚类数量并计算聚类原型。

　　我们建立了一个狄利克雷过程混合模型（Dirichlet Process Mixture Model (DPMM)），并假设节点表示的分布是一个高斯混合模型（GMM），其分量具有相同的固定协方差矩阵$\sigma \mathbf{I}$。每个组件都用于建模一个 cluster 的原型。DPMM 模型可以定义为：

　　　　$\begin{array}{llrl}G & \sim \operatorname{DP}\left(G_{0}, \alpha\right) & & \\\phi_{i} & \sim G & & \text { for } i=1, \ldots, N \\\mathbf{h}_{i} & \sim \mathcal{N}\left(\phi_{i}, \sigma \mathbf{I}\right) & & \text { for } i=1, \ldots, N\end{array}\quad\quad\quad(5)$

　　其中：

• • $G$ 是由狄利克雷过程 $\operatorname{DP}\left(G_{0}, \alpha\right) $ 得到的高斯分布；　　
  • $\alpha$ 是 $\operatorname{DP}\left(G_{0}, \alpha\right)$ 的浓度参数；　　
  • $\phi_{i}$ 是节点表示的高斯采样的均值；　　
  • $ G_{0} $ 是高斯分布的的先验均值，本文取 $G_{0}$ 为一个零均值高斯 $\mathcal{N}(\mathbf{0}, \rho \mathbf{I})$；
  • $\rho \mathbf{I}$ 是协方差矩阵；

　　接下来，我们使用一个折叠的 $\text{collapsed Gibbs sampler }$ 用 DPMM来推断 GMM 的组件。$\text{Gibbs sampler }$对给定高斯分量均值的节点的伪标签进行迭代采样，并对给定节点的伪标签的高斯分量的均值进行采样。当高斯分量 $\sigma \rightarrow 0$ 的方差变化时，对伪标签进行采样的过程变得确定性的。设 $\tilde{K}$ 表示当前迭代步骤中推断出的原型数量，原型分配更新可以表述为：

　　　　$z_{i}=\underset{k}{\arg \min }\left\{d_{i k}\right\}, \quad \text { for } i=1, \ldots, N$

　　　　$d_{i k}=\left\{\begin{array}{ll} \left\|\mathbf{h}_{i}-\mathbf{c}_{k}\right\|^{2} & \text { for } k=1, \ldots, \tilde{K} \\ \xi & \text { for } k=\tilde{K}+1 \end{array}\right.\quad\quad\quad(6)$

　　其中，$d_{i k}$ 是确定节点表示 $\mathbf{h}_{i}$ 的伪标签的度量。$ \xi $ 是初始化一个新原型的边际。在实践中，我们通过对每个数据集进行交叉验证来选择 $ \xi $ 的值。根据 $\text{Eq.6}$ 中的公式，将一个节点分配给由最近高斯均值对应的分量建模的原型，除非到最近均值的平方欧氏距离大于 $ \xi $。在获得伪标签后，可以通过以下方法计算集群原型表示：

　　　　${\large \mathbf{c}_{k}=\frac{\sum\limits _{z_{i}=k} \mathbf{h}_{i}}{\sum\limits_{z_{i}=k} 1}} , \quad \text { for } k=1, \ldots, \tilde{K}\quad\quad\quad(7)$

　　注意，我们迭代地更新原型分配和原型表示直到收敛，然后我们将原型的数量 $K$ 设置为推断出的原型的数量 $\tilde{K}$。原型推理的算法在附录中总结为 Algorithm 2。

3.2.2 Prototype Refinement via Label Propagation

　　考虑到贝叶斯非参数算法推断出的伪标签可能不准确，我们进一步基于标签传播对 Gibbs sampler 生成的伪标签进行了重新细化。通过这种方法，我们可以平滑噪声伪标签，并利用结构知识改进聚类原型表示。

　　首先，我们将原型赋值 $\mathcal{Z}$ 转换为一个单热的伪标签矩阵 $\mathbf{Z} \in \mathbb{R}^{N \times K}$ ，其中 $\mathbf{Z}_{i j}=1$ 当且仅当 $z_{i}=k$。根据个性化PageRank(PPR)的想法，$T $ 聚合步后 $\mathbf{Z}^{(T)}$ 的伪标签更新为：

　　　　$\mathbf{Z}^{(t+1)}=(1-\beta) \tilde{\mathbf{A}}_{s y m} \mathbf{Z}^{(t)}+\beta \mathbf{Z}^{(0)}\quad\quad\quad(8)$

　　其中，$ \mathbf{Z}^{(0)}=\mathbf{Z}$ 和 $\beta$ 可以视为 PPR 中的转移概率。接下来，我们通过设置 $z_{i}=   \arg \max _{k} \mathbf{Z}_{i k}^{(T)}$  $i \in\{1, \ldots, N\}$ ，将传播的结果 $i \in\{1, \ldots, N\}$  转换为硬伪标签。

　　在使用标签传播对伪标签 $\mathcal{Z}$ 进行细化后，我们使用每个集群中节点表示的平均值作为集群原型表示，由$\mathbf{c}_{k}=\sum_{z_{i}=k} \mathbf{h}_{i} / \sum_{z_{i}=k} 1$ 计算出。

3.2.3 Semantic Contrastive Objective

　　给定原型分配 $\mathcal{Z}$ 和原型表示 $\mathbf{C}$，我们的语义对比学习旨在找到网络参数 $\theta$，最大化对数似然定义为：

　　　　$Q(\boldsymbol{\theta})=\sum\limits _{i=1}^{N} \log p\left(\mathbf{x}_{i} \mid \boldsymbol{\theta}, \mathbf{C}\right)\quad\quad\quad(9)$

　　其中 $p$ 是概率密度函数。作为 $p\left(\mathbf{x}_{i} \mid \boldsymbol{\theta}, \mathbf{C}\right)= \sum_{k=1}^{K} \log p\left(\mathbf{x}_{i}, z_{i}=k \mid \boldsymbol{\theta}, \mathbf{C}\right)$，我们得到

　　　　$Q(\boldsymbol{\theta})=\sum\limits _{i=1}^{N} \sum\limits _{k=1}^{K} \log p\left(\mathbf{x}_{i}, z_{i}=k \mid \boldsymbol{\theta}, \mathbf{C}\right)\quad\quad\quad(10)$

　　$Q(\boldsymbol{\theta})$ 的变分下界由

　　　　$\begin{aligned}Q(\boldsymbol{\theta}) & \geq \sum\limits_{i=1}^{N} \sum\limits_{k=1}^{K} q\left(k \mid \mathbf{x}_{i}\right) \log \frac{p\left(\mathbf{x}_{i}, z_{i}=k \mid \boldsymbol{\theta}, \mathbf{C}\right)}{q\left(k \mid \mathbf{x}_{i}\right)} \\&=\sum\limits_{i=1}^{N} \sum\limits_{k=1}^{K} q\left(k \mid \mathbf{x}_{i}\right) \log p\left(\mathbf{x}_{i}, z_{i}=k \mid \boldsymbol{\theta}, \mathbf{C}\right) -\sum\limits_{i=1}^{N} \sum\limits_{k=1}^{K} q\left(k \mid \mathbf{x}_{i}\right) \log q\left(k \mid \mathbf{x}_{i}\right)\end{aligned}\quad\quad\quad(11)$

　　其中，$q\left(k \mid \mathbf{x}_{i}\right)=p\left(z_{i}=k \mid \mathbf{x}_{i}, \boldsymbol{\theta}, \mathbf{C}\right)$ 表示 $z_{i}$ 的后部。由于上面的第二项是一个常数，我们可以通过最小化函 数 $E(\boldsymbol{\theta})$ 来最大化对数似然 $Q(\boldsymbol{\theta})$，如下：

　　　　$E(\boldsymbol{\theta})=-\sum\limits_{i=1}^{N} \sum\limits_{k=1}^{K} q\left(k \mid \mathbf{x}_{i}\right) \log p\left(\mathbf{x}_{i}, z_{i}=k \mid \boldsymbol{\theta}, \mathbf{C}\right)\quad\quad\quad(12)$

　　通过让 $q\left(k \mid \mathbf{x}_{i}\right)=\mathbb{1}_{\left\{z_{i}=k\right\}}$，$E(\boldsymbol{\theta})$ 可以通过 $-\sum_{i=1}^{N} \log p\left(\mathbf{x}_{i}, z_{i} \mid \boldsymbol{\theta}, \mathbf{C}\right)$ 来计算。在 $\mathbf{x}_{i}$ 在不同原型上的先验分布均匀的假设下，我们有$p\left(\mathbf{x}_{i}, z_{i} \mid \boldsymbol{\theta}, \mathbf{C}\right) \propto p\left(\mathbf{x}_{i} \mid z_{i}, \boldsymbol{\theta}, \mathbf{C}\right)$ 。由我们的DPMM模型生成的每个原型周围的分布是一个高斯分布。如果我们在节点和原型的表示上应用 $\ell_{2}$ 归一化，我们可以估计$p\left(\mathbf{x}_{i} \mid z_{i}, \boldsymbol{\theta}, \mathbf{C}\right)$ 通过：

　　　　$p\left(\mathbf{x}_{i} \mid z_{i}, \boldsymbol{\theta}, \mathbf{C}\right)=\frac{\exp \left(\mathbf{h}_{i} \cdot \mathbf{c}_{z_{i}} / \tau_{2}\right)}{\sum\limits _{k=1}^{K} \exp \left(\mathbf{h}_{i} \cdot \mathbf{c}_{k} / \tau_{2}\right)}\quad\quad\quad(13)$

　　其中，$ \tau_{2} \propto \sigma^{2}$ 和 $ \sigma$ 为 Eq.5 定义的DPMM模型中高斯分布的方差。$\mathbf{h}_{i}$ 和 $\mathbf{c}_{z_{i}}$ 是 $\mathbf{x}_{i}$ 和 $z_{i} -th$ 原型的代表。因此，$ E(\boldsymbol{\theta})$ 可以通过最小化损失函数来最小化，如下：

　　　　$\mathcal{L}_{s e m}=-\frac{1}{N} \sum\limits _{i=1}^{N} \log \frac{\exp \left(\mathbf{h}_{i} \cdot \mathbf{c}_{z_{i}} / \tau_{2}\right)}{\sum\limits _{k=1}^{K} \exp \left(\mathbf{h}_{i} \cdot \mathbf{c}_{k} / \tau_{2}\right)}\quad\quad\quad(14)$

　　Algorithm 1

　　

4.3 Model Learning

4.3.1 Overall Loss

　　为了以端到端方式训练我们的模型，并学习编码器$f_{\theta}(\cdot)$，我们共同优化了结构和语义对比学习损失。总体目标函数的定义为：

　　　　$\mathcal{L}=\gamma \mathcal{L}_{s t r}+(1-\gamma) \mathcal{L}_{s e m}\quad\quad\quad(15)$

　　我们的目标是在训练中最小化 $\mathcal{L}$，$\gamma$ 是一个平衡因素来控制每个损失的贡献。

　　值得注意的是，在语义对比学习中，计算出的伪标签 $ \mathcal{Z}$ 可以用于负示例抽样过程，以避免结构对比学习中的抽样偏差问题。我们从分配给不同原型的节点中，在 Eq.3 中为每个节点选择负样本。对负示例抽样的详细分析见附录C.2。

4.3.2 Model Optimization via EM

　　采用EM算法交替估计后验分布 $p\left(z_{i} \mid \mathbf{x}_{i}, \boldsymbol{\theta}, \mathbf{C}\right)$，并优化网络参数$\boldsymbol{\theta}$。我们描述了在我们的方法中应用的 $E-step$ 和 $M-step$ 的细节如下：

E-step

　　在这一步中，我们的目标是估计后验分布$p\left(z_{i} \mid \mathbf{x}_{i}, \boldsymbol{\theta}, \mathbf{C}\right) $。为了实现这一点，我们修复网络参数$\boldsymbol{\theta}$，估计原型 $\mathbf{C} $ 和原型分配 $\mathcal{Z}$为了训练编码器网络的稳定性，我们应用贝叶斯非参数原型推理算法的节点表示计算动量编码器$\mathbf{H}^{\prime}=f_{\theta^{\prime}}(\tilde{\mathbf{X}})$，动量编码器的$\boldsymbol{\theta}^{\prime}$参数$\boldsymbol{\theta}$的移动平均更新：

　　　　$\boldsymbol{\theta}^{\prime}=(1-m) \cdot \boldsymbol{\theta}+m \cdot \boldsymbol{\theta}^{\prime}\quad\quad\quad(16)$

　　其中：

　　　　$m \in[0,1)$ 是动量系数

M-step

　　给定由 E-step 计算的后验分布，我们的目标是通过直接优化语义对比损失函数Lsem来最大化对数似然 $Q(\boldsymbol{\theta})$ 的期望。为了同时执行结构对比学习和语义对比学习，我们优化了一个如 Eq.15 所示的联合整体损失函数。

　　在对未标记的输入图进行自我监督的预训练后，预训练的编码器可以直接用于生成各种下游任务的节点表示。

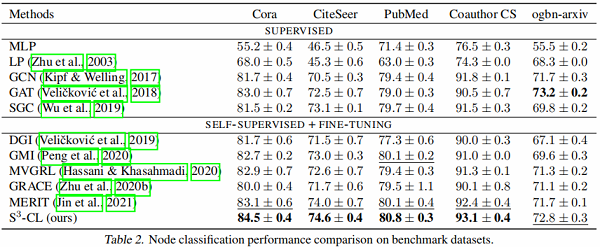
5 Experiments

5.1 数据集

　　

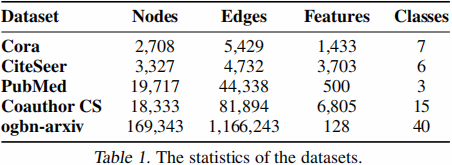
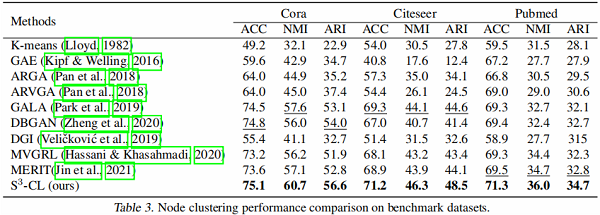
5.2 实验结果