论文信息
论文标题:Graph Representation Learning via Contrasting Cluster Assignments
论文作者:Chun-Yang Zhang, Hong-Yu Yao, C. L. Philip Chen, Fellow, IEEE and Yue-Na Lin
论文来源:2022, TKDE
论文地址:download
论文代码:download
1 介绍
我们提出了一种新的无监督图表示学习模型,通过对比聚类分配,称为GRCCA。为了避免极度关注局部或全局视图,GRCCA将聚类算法和对比学习与相反的增广策略相结合,以获得两个视图的平衡。它利用聚类来获取更细粒度的全局信息(cluster-level ),并在节点级对嵌入进行对齐,以保持局部信息的质量,从而优雅地融合局部信息和全局信息。相反的增强策略进一步增强了全局和局部视图的对比度,使模型从图中挖掘出更不变的特征。同时,聚类使模型能够深入了解节点之间的潜在关联,而不仅仅是拓扑邻近性。为了证明其有效性,我们在三种不同的下游任务中与最先进的模型进行了比较,包括节点分类、链接预测和社区检测。实验结果表明,GRCCA在大多数任务中都具有较强的竞争力。
2 方法
在本节中,将分两部分详细阐述所提出的 GRCCA。第一部分介绍 GRCCA 的总体框架,包括图的增强策略和模型结构。第二部分详细描述了该学习算法。
2.1 定义
图 $G=(V,E)$,其中 $V$ 是节点集合,$E \subseteq V \times V$ 表示边集合。邻接矩阵 $A \in\{0,1\}^{N \times N}$,其中 $N$ 是节点数量和 $A_{i j}=1$ 表示 $ \left(v_{i}, v_{j}\right) \in \mathcal{E}$ ,节点属性信息由属性矩阵 $X \in \mathbb{R}^{N \times F}$ 表示。
目的:不使用标签信号学习一个图编码 $f_{\theta}: \mathbb{R}^{N \times F} \times \mathbb{R}^{N \times N} \rightarrow \mathbb{R}^{N \times F^{\prime}}$ ,即 $H=f_{\theta}(X, A) \in \mathbb{R}^{N \times F^{\prime}}$,其中 $F^{\prime} \ll F$。学习到的嵌入可以用于下游任务,如节点分类、链接预测等。
2.2 总体框架
本文的数据增强策略:【数据增强策略的要求:既可以生成多个视图,又不会产生噪声】
-
- Graph Diffusion (GD)
- Removing Edges (RE)
本文分别使用 Graph Diffusion (GD) 和 Removing Edges (RE) 来关注全局视图和局部视图。这两种方法都是基于图的拓扑结构,并没有引入新的噪声。
框架如下:

2.2.1 Graph Diffusion (GD)
Graph diffusion 研究了超过 $\text{1-hop}$ 的信息传递,从而可以获得节点的长期依赖。
图扩散过程定义为:
$S=\sum\limits _{k=0}^{\infty} \theta_{k} T^{k}\quad\quad\quad(1)$
其中:
-
- $T$ 代表广泛的转移矩阵,$\mathbf{T}=\mathbf{D}^{-1 / 2} \mathbf{A} \mathbf{D}^{-1 / 2}$ ;
- ${\theta }_{k}$ 代表了权重参数,${\theta }_{k}=\alpha(1-\alpha)^{k}$,$\sum\limits _{k=0}^{\infty} \theta_{k}=1$, $\theta_{k} \in[0,1]$;
PPR kernel 可以由下式表达:
$S=\alpha\left(I-(1-\alpha) D^{-1 / 2} A D^{-1 / 2}\right)^{-1} \quad\quad\quad\quad(2)$
其中:
-
- $\alpha \in(0,1)$ 是随机游走的传送概率
2.2.2 Removing Edges (RE)
具体地说,给定一个相邻矩阵 $A$ 和边删除概率 $P_{r e}$,我们随机去除现有的边,可以定义为
$\widetilde{A}_{i j}=\left\{\begin{array}{ll} 1, & b_{i j}<P_{r e} \text { and } A_{i, j}=1 \\ 0, & \text { otherwise } \end{array}\right.\quad\quad\quad(3)$
其中,$ \widetilde{A} $ 是局部水平的增强,$b$ 表示从均匀分布$ U(0,1)$中抽样的随机数。
2.2.3 Masking Nodes Features (MNF)
为获得图属性的不同视角,我们给定一个属性矩阵 $X$ 和掩蔽矩阵 $P_{m n f}$ ,我们随机选择属性的维数来掩蔽,而不是单独掩蔽每个节点,可以表示为:
$\tilde{X}_{i}=X_{i} \odot M\quad\quad\quad\quad(4)$
其中$ \tilde{X}$ 是属性增强矩阵,$ M \in\{0,1\}^{F}$是一个 $P_{m n f}$ 中一个百分比为零的向量。
该策略不会导致过度差异,因此不会破坏多个视角之间的关系,也不会将新的噪声带来对比学习。图的拓扑结构和属性策略不仅提供了多种多视图知识,而且进一步增强了全局视图和局部视图之间的对比。
2.2.4 表示学习
数据增强后,将生成的两个增广图输入共享图编码器 $f_{\theta}$ 和非线性投影仪 $g_{\theta}$,如 Fig. 1 所示。图表示学习的关键是同时保留拓扑结构和属性的信息。
理论上,任何考虑到这两个方面的模型都可以用作编码器$f_{\theta}$。现有的图编码器大多是基于邻域聚合的。通过多层邻域信息聚合,它们可以捕获长期图信息,由
$\mathbf{h}_{v}^{k}=\sigma\left(\mathcal{E} \cdot \mathbf{h}_{v}^{k-1}+\mathbf{W} \cdot \sum\limits _{u \in N(v)} h_{u}^{k-1} /|N(v)|\right)\quad\quad\quad(5)$
其中 $\mathcal{E}$ 和 $\mathbf{W}$ 为可学习参数,$\sigma$ 为激活函数,$N(v)$ 表示目标节点 $v$ 的邻域节点。
本文以 GCN 为实例,获得节点嵌入$H=f_{\theta}(X, A) $,它可以被定义为
$H=\sigma\left(\hat{D}^{-1 / 2} \hat{A} \hat{D}^{-1 / 2} X \Theta\right)\quad\quad\quad(6)$
为了增强对比学习的表达能力,我们进一步利用一个非线性投影仪,即MLP,将节点嵌入转移到一个度量空间中,即 $Z=g_{\theta}(H) \in \mathbb{R}^{N \times F^{\prime}}$。
2.3 Learning Algorithm
GRCCA 将对比学习和聚类算法结合在一起,从两个增强的角度最大化相同节点之间的 cluster-level 的一致性。对比聚类分配不仅促进了对比学习和聚类算法之间的合作,而且还提供了一种理想的方法来协调局部和全局视图。
获得两个视图的表示 $Z_{v}$ 和 $Z_{u}$ 后,然后应用 k-means ,分别得到各自的聚类中心矩阵 $C_{v} \in \mathbb{R}^{K \times F^{\prime}}$ 和 $C_{u} \in \mathbb{R}^{K \times F^{\prime}} $($K$ 代表这 cluster 数目)。进一步计算两个视图各自的聚类分配矩阵 $Q_{v}$ 和 $Q_{u}$【 $q_{v_{i}}=\mathbb{I}_{z_{v_{i}} \in C_{v}^{K}} $ 或 $q_{u_{i}}=\mathbb{I}_{z_{u_{i}} \in C_{u}^{K}}$】。
为了在两个视图之间实现 cluster-level 对比学习,提出的 GRCCA 通过最小化交叉熵损失,从不同角度强制相同的节点来识别彼此的聚类分配。例如,给定任意一对相同的节点 $v_i$ 和 $u_i$,节点 $v_i$ 和节点 $u_i$ 的聚类分配 $Q_{u_{i}}$ 之间的一致性可以定义为:
$p_{v_{i}}=\operatorname{softmax}\left(z_{v_{i}} C_{u}^{\mathrm{T}} / \tau\right)\quad\quad\quad(7)$
与以往的图对比学习模型和基于聚类的图表示学习模型不同,GRCCA将对比学习和聚类算法结合在一起,从两个增强的角度最大化相同节点之间的 cluster-level 的一致性。
通过最小化交叉熵损失,保证了节点之间的一致性:
$\ell\left(q_{u_{i}}, p_{v_{i}}\right)=-q_{u_{i}} \log p_{v_{i}}\quad\quad\quad(8)$
因此,对比聚类损失可以定义为:
$\mathcal{L}_{c}=\frac{1}{N} \sum\limits _{i=0}^{N}\left[\ell\left(q_{v_{i}}, p_{u_{i}}\right)+\ell\left(q_{u_{i}}, p_{v_{i}}\right)\right]\quad\quad\quad(9)$
其中,$N$ 为节点数。值得注意的是,对比聚类分配可以被视为一种特殊的对比学习方式,它可以比较多个图视角之间的聚类分配,而不是节点嵌入。它隐式地驱动节点嵌入来接近它们相应的原型,并与其他原型区分开来。直观地说,它等价于最大化节点嵌入和相应的原型之间的互信息。
受多头注意力机制的启发,GRCCA采用了 multi-clustering strategy 来增加 cluster-level 信息的多样性。具体来说,我们对每个视图同步执行多个聚类,生成多个成对对比材料 $\left\{\left(C_{v}^{1}, C_{u}^{1}, Q_{v}^{1}, Q_{u}^{1}\right), \ldots,\left(C_{v}^{h}, C_{u}^{h}, Q_{v}^{h}, Q_{u}^{h}\right)\right\}$,并利用对比聚类分配来确保其聚类水平的一致性。因此,总损失可以由
$\mathcal{L}_{m c}=\frac{1}{h} \sum_{i=0}^{h} \mathcal{L}_{c}^{i}\quad\quad\quad(10)$
其中,$h$ 为对比材料的个数。
该学习算法总结在 Algorithm 1中:

首先,我们应用两个图增广函数 $t_{1} \sim T$ 和 $t_{2} \sim T$ 生成两个增广图 $\widetilde{G}_{1}$ 和 $\widetilde{G}_{2}$,其中 $t_{1}$ 由 GD 和 MNF 组成,$t_{2}$ 包括 RE 和 MNF。其次,我们使用图编码器 $f_{\theta}$ 和非线性投影仪 $g_{\theta}$ 分别生成两个视图的节点表示。第三,利用具有多聚类策略 $K_{m}$ 的 k-means 生成聚类分配 $Q_{v}$、$Q_{u}$ 和原型 $C_{v}$、$C_{u}$。第四,我们最小化了 Eq. (10) 中的对比损失,可以从不同的角度来加强相同节点之间的 cluster-level 一致性。否则,我们将尝试两种不同的集群分配方案:异步版本和同步版本。异步版本使用来自前一个 epoch 的表示矩阵来生成集群分配,而同步版本则使用当前的表示矩阵。值得注意的是,异步版本需要初始化一个memory bank $B$,并使用每一轮表示来更新它。最后,将从图编码器 $f_{\theta}$ 中学习到的节点嵌入用于下游任务。
3 Experiments
3.1 Datasets

-
- Cora,Citeseer 和 Pubmed 都是 citation networks
- Amazon-Photo 和 Amazon-Computers 是两个co-purchase graphs
- Coauthor-CS 是一个 co-authorship graph
3.2 Node Classification
我们选择了6个最先进的无监督模型,包括DGI,GMI,MVGRL,GIC,GCA和MERIT,以及3个经典的GNN模型:ChebyshevGCN,GCN,和 GAT 作为基线。
对于三个引文网络,我们对每个类随机抽取20个节点来形成训练集,1000个节点作为测试集。而对于其他三个数据集,我们对每个类分别随机选择30个节点进行训练和验证,其余的节点用于测试。
超参数设置:
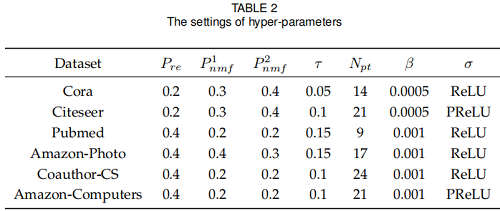
结果:
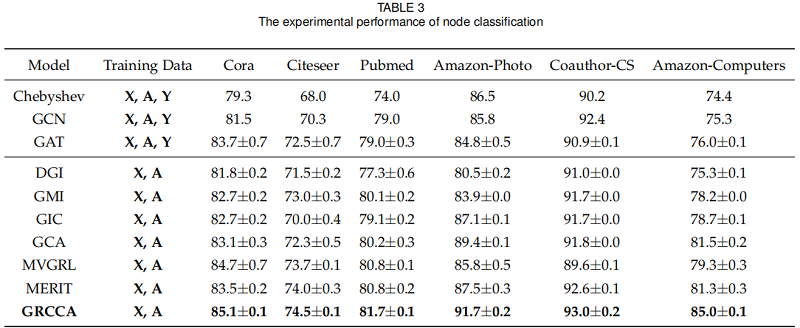
3.3 Link Prediction
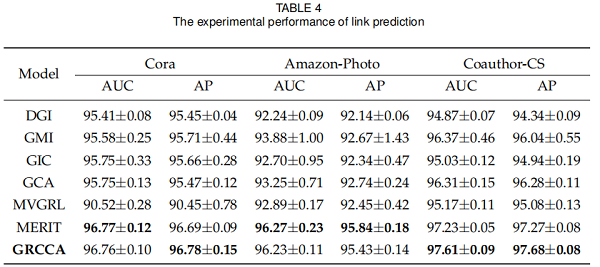
3.4 Community Detection
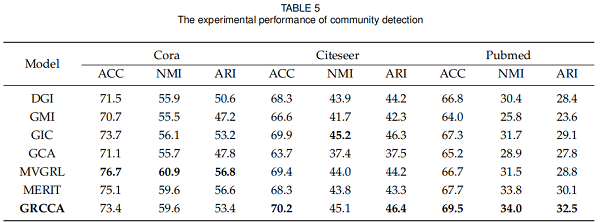
3.5 Ablation Study
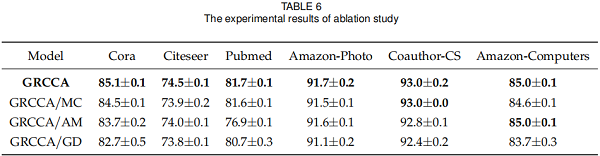
3.6 Complexity Analysis
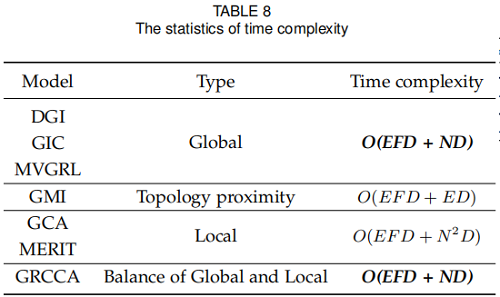
可学习参数的数量