论文信息
论文标题:Self-supervised Learning on Graphs: Contrastive, Generative,or Predictive
论文作者:Lirong Wu, Haitao Lin, Cheng Tan,Zhangyang Gao, and Stan.Z.Li
论文来源:2022, ArXiv
论文地址:download
1介绍
图深度学习的发展是由于能够捕获图的结构和节点/边特征。
大多数的工作都集中在有监督或半监督学习,其中模型由特定的下游任务和丰富的标记数据进行训练,这是有限的,昂贵的,和难以接近的。这些方法容易出现过拟合、泛化差和鲁棒性弱等问题。
SSL的主要目标是通过精心设计的代理任务,从丰富的未标记数据中学习可转移的知识,然后将学习到的知识推广到具有监督的下游任务中。
为什么SSL应用到图中具有深刻的意义:
-
- 首先,除了节点特征外,图数据还包含了结构,其中可以设计大量的代理任务来捕获节点之间的内在关系;
- 其次,真实世界的图通常是由特定的规则组成的,因此,可以将许多先验知识纳入到代理任务的设计中;
- 最后,图数据一般支持直推式学习,如节点分类,在训练中训练样本/验证样本/测试样本的特征在训练过程中都可用,这使得设计更多与特征相关的代理任务成为可能;
SSL在图数据上的挑战
-
- 首先,大部分预训练方法是基于 grid-like 结构的数据,而图上的数据通常是 structured-like ;
- 其次,许多预训练方法的数据通常满足 iid. 条件,而图上的数据不满足 iid. 条件,即图数据之间存在依赖关系(边);
- 最后,由于SSL的代理任务与下游任务优化目标的差异,这种差异损害了泛化性;
2 问题阐述
2.1 概念和定义
- Definition 1 (Graph): We use $g=(\mathcal{V}, \mathcal{E})$ to denote a graph where $\mathcal{V}$ is the set of $N$ nodes and $\mathcal{E}$ is the set of $M$ edges. Let $v_{i} \in \mathcal{V}$ denote a node and $e_{i, j}$ denote an edge between node $v_{i}$ and $v_{j}$ . The l -hop neighborhood of a node $v_{i}$ is denoted as $\mathcal{N}_{i}^{(l)}=\left\{v_{j} \in \mathcal{V} \mid d\left(v_{i}, v_{j}\right) \leq l\right\}$ where $d\left(v_{i}, v_{j}\right)$ is the shortest path length between node $v_{i}$ and $v_{j}$ . In particular, the 1-hop neighborhood of a node $v_{i}$ is denoted as $\mathcal{N}_{i}=\mathcal{N}_{i}^{(1)}=\left\{v_{j} \in \mathcal{V} \mid e_{i, j} \in \mathcal{E}\right\} $. The graph structure can also be represented by an adjacency matrix $\mathbf{A} \in[0,1]^{N \times N}$ with $\mathbf{A}_{i, j}=1$ if $e_{i, j} \in \mathcal{E}$ and $\mathbf{A}_{i, j}=0$ if $e_{i, j} \notin \mathcal{E}$ .
- Definition 2 (Attribute Graph): Attributed graph, an opposite concept to the unattributed one, refers to a graph where nodes or edges are associated with their own features (a.k.a, attributes). For example, each node $v_{i}$ in graph g may be associated with a feature vector $\mathbf{x}_{i} \in \mathbb{R}^{d_{0}} $, such a graph is referred to an attributed graph $g=(\mathcal{V}, \mathcal{E}, \mathbf{X})$ or $g=(\mathbf{A}, \mathbf{X})$ , where $\mathbf{X}=\left[\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{N}\right]$ is the node feature matrix. Meanwhile, an attributed graph $g=\left(\mathcal{V}, \mathcal{E}, \mathbf{X}^{e}\right)$ may have edge attributes $\mathbf{X}^{e}$ , where $\mathbf{X}^{e} \in \mathbb{R}^{M \times b_{0}}$ is an edge feature matrix with $\mathbf{x}_{i, j}^{e} \in \mathbb{R}^{b_{0}}$ being the feature vector of edge $e_{i, j}$ .
- Definition 3 (Dynamic Graph): A dynamic graph is a special attributed graph where the node set, graph structure and node attributes may change dynamically over time. The dynamic graph can be formalized as $g=\left(\mathcal{V}^{(t)}, \mathcal{E}^{(t)}, \mathbf{X}^{(t)}\right)$ or $g=\left(\mathbf{A}^{(t)}, \mathbf{X}^{(t)}\right)$ , where $\mathcal{E}^{(t)}$ represents the edge set at the time step $t$ and $\mathbf{A}_{i, j}^{(t)}=1$ denotes an interaction between node $v_{i}$ and $ v_{j}$ at the time step $t(1 \leq t \leq T)$ .
- Definition 4 (Heterogeneous Graph): Consider a graph $g= (\mathcal{V}, \mathcal{E})$ with a node type mapping function $f_{v}: \mathcal{V} \rightarrow \mathcal{Y}^{v}$ and an edge type mapping function $f_{e}: \mathcal{E} \rightarrow \mathcal{Y}^{e}$ , where $\mathcal{Y}^{v}$ is the set of node types and $\mathcal{Y}^{e}$ is the set of edge types. For a graph with more than one type of node or edge, e.g., $\left|\mathcal{Y}^{v}\right|>1$ or $\left|\mathcal{Y}^{e}\right|>1$ , we define it as a heterogeneous graph, otherwise, it is a homogeneous graph. There are some special types of heterogeneous graphs: a bipartite graph with $\left|\mathcal{Y}^{v}\right|=2$ and $\left|\mathcal{Y}^{e}\right|=1$ , and a multiplex graph with $\left|\mathcal{Y}^{v}\right|=1$ and $\left|\mathcal{Y}^{e}\right|>1$ .
- Definition 5 (Spatial-Temporal Graph): A spatial-temporal graph is a special dynamic graph, but noly the node attributes change over time with the node set and graph structure unchanged. The spatial-temporal graph is defined as $g=\left(\mathcal{V}, \mathcal{E}, \mathbf{X}^{(t)}\right)$ or $g=\left(\mathbf{A}, \mathbf{X}^{(t)}\right)$ , where $\mathbf{X}^{(t)} \in \mathbb{R}^{N \times d_{0}}$ is the node feature matrix at the time step $t(1 \leq t \leq T)$ .
2.2 下游任务(Downstream Tasks)
图上的下游任务可以分为三类:
-
- node-level
- link-level
- graph-level tasks
节点级图编码器 $f_{\theta}(\cdot)$ 通常用于生成每个节点的节点嵌入,而图级图编码器 $f_{\gamma}(\cdot)$ 通常用于生成图级嵌入。最后,将学习到的嵌入输入一个可选的预测头$g_{\omega}(\cdot)$,以执行特定的下游任务。
2.2.1 节点级任务
常见的节点级任务:节点分类,即使用有标签节点集合,来预测没有标签的节点的类标。其对应的损失函数可以表达为:
$\underset{\theta, \omega}{\text{min}} \mathcal{L}_{\text {node }}(\mathbf{A}, \mathbf{X}, \theta, \omega)=\sum\limits _{\left(v_{i}, y_{i}\right) \in \mathcal{D}_{L}} \ell\left(g_{\omega}\left(\mathbf{h}_{i}\right), y_{i}\right)$
其中:
-
- $ \mathbf{H}=f_{\theta}(\mathbf{A}, \mathbf{X}) $ 且 $\mathbf{h}_{i}$ 是节点 $v_{i}$ 在嵌入矩阵 $H$ 中的嵌入表示;
- $\ell(\cdot, \cdot)$ 代表着分类的交叉熵函数;
2.2.2 图级别的任务
图级任务从一个数据集中的多个图中学习,并预测单个图的属性。举个图回归任务,即给定一些带属性有标签的图,学习一个 Encoder 去预测未知标记的图标签。对应的损失函数如下:
$\underset{\gamma, \omega}{\text{min}} \quad \mathcal{L}_{g r a p h}\left(\mathbf{A}_{i}, \mathbf{X}_{i}, \gamma, \omega\right)=\sum\limits _{\left(g_{i}, p_{i}\right) \in \mathcal{D}_{L}} \ell\left(g_{\omega}\left(\mathbf{h}_{g_{i}}\right), p_{i}\right)$
其中
-
- $\mathbf{h}_{g_{i}}=f_{\gamma}(\mathbf{A}, \mathbf{X})$ 是图$g_{i}$ 的图嵌入表示;
- $g_{\omega}(\cdot)$ 将图嵌入表示映射到一维;
- $\ell(\cdot, \cdot)$ 代表MSE损失;
2.3 图神经网络
GNN 的两个部分:
-
- AGGREGATE operation:聚合来自邻域 $\mathcal{N}_{i}$ 的消息;
- UPDATE operation:从节点在上一层的表示和聚合消息更新节点表示;
考虑GNN第的 $\text{L}$ 层:
$\begin{aligned} \mathbf{a}_{i}^{(l)} &=\mathrm{AGGREGATE}^{(l)}\left(\left\{\mathbf{h}_{j}^{(l-1)}: v_{j} \in \mathcal{N}_{i}\right\}\right) \\ \mathbf{h}_{i}^{(l)} &=\mathrm{UPDATE}^{(l)}\left(\mathbf{h}_{i}^{(l-1)}, \mathbf{a}_{i}^{(l)}\right) \end{aligned}$
对于节点级任务、边级任务,通常可以直接使用 $\mathbf{h}_{i}^{(L)}$,而对于图级别的任务,则需要进一步使用 READOUT 函数,来获得图级别的表示:
$\mathbf{h}_{g}=\operatorname{READOUT}\left(\left\{\mathbf{h}_{i}^{(L)} \mid v_{i} \in \mathcal{V}\right\}\right)$
2.4 训练策略
关于训练策略有三种:
-
- Pre-training and Fine-tuning (P&F)
- Joint Learning (JL)
- Unsupervised Representation Learning (URL)
2.4.1 预训练和微调 Pre-training and Fine-tuning (P&F)
框架如下:
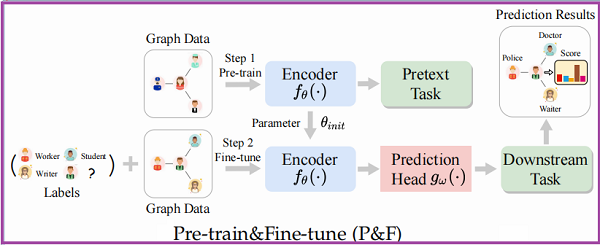
首先它是一个两阶段框架,预训练:其中的 Encoder $f_{\theta}(\cdot)$ 是通过代理任务预训练得到的,然后预训练得到的参数 $\theta_{\text {init }} $ 将作为 Encoder $f_{\theta_{i n i t}}(\cdot) $ 初始化参数;微调阶段,$f_{\theta_{i n i t}}(\cdot) $ 则是在某具体的下游任务,通过投影头$g_{\omega}(\cdot)$ 进行微调。
学习目标被表述为:
$\theta^{*}, \omega^{*}=\underset{(\theta, \omega)}{\text{arg min}} \mathcal{L}_{\text {task }}\left(f_{\theta_{i n i t}}, g_{\omega}\right)$
其中:
-
- $\theta_{\text {init }}=\arg \min _{\theta} \mathcal{L}_{s s l}\left(f_{\theta}\right)$
- $\mathcal{L}_{\text {task }}$ 和 $\mathcal{L}_{s s l}$ 分别是下游任务的损失函数和自监督预训练任务的损失函数
2.4.2 联合训练 Joint Learning
框架如下:
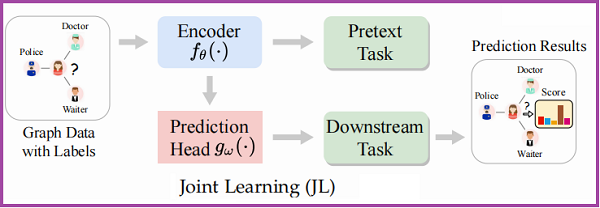
在该方案中,Encoder $f_{\theta}(\cdot)$ 在代理任务和下游任务的监督下,与预测头 $g_{\omega}(\cdot) $ 进行联合训练。Joint Learning 策略也可以看作是一种多任务学习,或者将代理任务作为一种正则化学习。学习目标被表述为:
$\theta^{*}, \omega^{*}=\underset{(\theta, \omega)}{\text{arg min}} \mathcal{L}_{\text {task }}\left(f_{\theta}, g_{\omega}\right)+\alpha \arg \min _{\theta} \mathcal{L}_{s s l}\left(f_{\theta}\right)$
其中:$\alpha$ 是一个 trade-off 参数。
2.4.3 无监督表示学习 Unsupervised Representation Learning
框架如下:
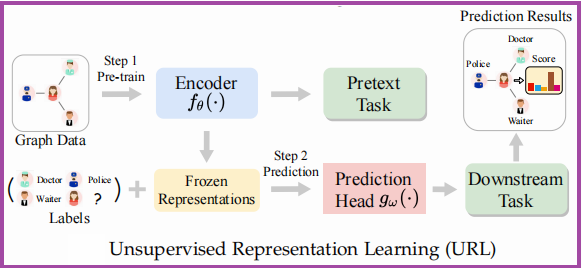
这种策略也可以被认为是一个两阶段的方法,第一阶段类似与 Pre-training 框架;第二阶段中输入的不在是图数据而是冻结的表示,通过下游任务进行训练。学习目标被表述为:
$\omega^{*}=\underset{( \omega)}{\text{arg min}} \mathcal{L}_{\text {task }}\left(f_{\theta_{i n i t}}, g_{\omega}\right)$
其中:
-
- $\theta_{\text {init }}=\underset{\theta}{\text{arg min}} \mathcal{L}_{s s l}\left(f_{\theta}\right)$