论文解读（GRACE）《Deep Graph Contrastive Representation Learning》 Learner

Paper Information

论文标题：Deep Graph Contrastive Representation Learning
论文作者：Yanqiao Zhu, Yichen Xu, Feng Yu, Q. Liu, Shu Wu, Liang Wang
论文来源：2020, ArXiv
论文地址：download 
代码地址：download

Abstract

　　在本文中，作者提出了一个利用节点级对比目标的无监督图表示学习框架。具体来说，通过破坏原始图去生成两个视图，并通过最大化这两个视图中节点表示的一致性来学习节点表示。

　　为了为对比目标提供不同的节点上下文，提出了一种在结构和属性层次上生成视图的混合方案。

　　此外，作者从互信息和三元组损失（ triplet loss）两个角度提供了理论证明。并使用真实的数据集对归纳式和直推式学习任务进行了实验。

1 Introduction

　　图表示学习的目的是学习一个编码函数，将节点转换为低维密集嵌入，以保留图的属性和结构特征。

　　阐述 DGI 的缺点：

• • DGI 使用平均池化的 readout 函数，不能保证图嵌入可以从节点中提取有用的信息，因为它不足以从节点级嵌入中保存独特的特征。
  • DGI 使用特征变换来生成损坏的视图。然而，该方案在生成负节点样本时，在粗粒度级别考虑损坏节点特征。当特征矩阵稀疏时，只执行特征变换不足以为损坏图中的节点生成不同的邻域（即上下文），导致对比目标的学习困难。

　　GRACE 框架如下：

　　

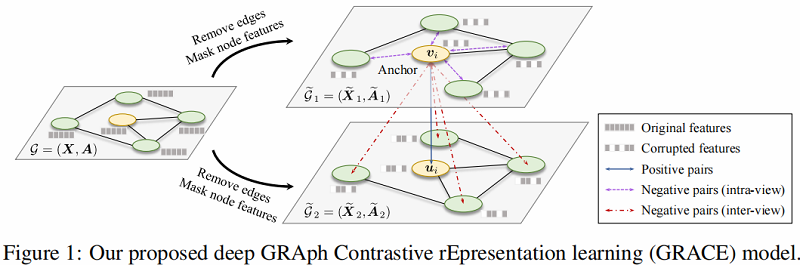
　　在本文提出的 GRACE 中，作者首先通过随机执行 corruption 来生成两个相关的视图。然后，使用对比损失来训练模型，以最大化这两个视图中节点嵌入之间的一致性。

　　对于如何进行 corruption ，本文从拓扑结构和节点属性考虑，即 removing edges 和 masking features ，以为不同视图中的节点提供不同的上下文，从而促进对比目标的优化。

　　贡献总结如下：

• • 首先，我们提出了一个用于无监督图表示学习的一般对比框架。所提出的 GRACE 框架简化了以前的工作，并通过最大化两个图视图之间的节点嵌入的一致性来进行工作。
    

• • 其次，我们提出了两种特定的方案，removing edges 和 masking features，以生成视图。
    
  • 最后，我们利用 6 个流行的公共基准数据集，在常用的线性评估协议下，对转换和归纳节点分类进行了全面的实证研究。GRACE 始终优于现有的方法，我们的无监督方法在转换任务上甚至超过了有监督的方法，展示了它在现实应用中的巨大潜力。

2 Related Work

　　Contrastive learning of visual representations

　　Graph representation learning

3 Deep Graph Contrastive Representation Learning

3.1 Preliminaries

　　$\mathcal{G}=(\mathcal{V}, \mathcal{E}), \mathcal{V}=\left\{v_{1}, v_{2}, \ldots, v_{N}\right\}, \mathcal{E} \subseteq \mathcal{V} \times \mathcal{V} $

　　特征矩阵: $\boldsymbol{X} \in \mathbb{R}^{N \times F}$，其中 $\boldsymbol{x}_{i} \in \mathbb{R}^{F} $ 。

　　邻接矩阵: $\boldsymbol{A} \in\{0,1\}^{N \times N} $ ，当 $ \left(v_{i}, v_{j}\right) \in \mathcal{E} $ 时， $\boldsymbol{A}_{i j}=1 $ 。

　　在训练过程中，没有给 $\mathcal{G}$ 的节点类别信息。

　　目标是学习一个 GNN 编码器 $f(\boldsymbol{X}, \boldsymbol{A}) \in \mathbb{R}^{N \times F^{\prime}} $ ，输入图的特征矩阵 $\boldsymbol{X}$ 和邻接矩阵 $\boldsymbol{A}$，输出低维节点嵌入，即 $ F^{\prime}<<F$。

　　将 $ \boldsymbol{H}=f(\boldsymbol{X}, \boldsymbol{A})$ 作为编码器学到的节点表示，其中 $\boldsymbol{h}_{i}$ 是节点 $v_{i}$ 的表示。这些表示可以用于下游任务中，如节点分类。

3.2 Contrastive Learning of Node Representations

3.2.1 The Contrastive Learning Framework

　　与之前利用 local-global 关系来学习表示的工作相反，在 GRACE 中，通过直接最大化节点表示之间的一致性来学习表示。

　　首先通过随机破坏原始图来生成两个视图。然后，采用一个对比目标使得在两个不同视图中对应节点彼此一致，并与其他节点的表示区分开来。

　　在 GRACE 模型中，每次迭代生成两个视图，分别为  $G_{1}$  和  $G_{2}$  。两个视图生成的节点表示分别为 $U=f\left(\widetilde{\boldsymbol{X}}_{1}, \widetilde{\boldsymbol{A}}_{1}\right) $ 和  $V=f\left(\widetilde{\boldsymbol{X}}_{2}, \widetilde{\boldsymbol{A}}_{2}\right) $ ， 其中  $\widetilde{\boldsymbol{X}}_{*} $ 和 $ \widetilde{\boldsymbol{A}}_{*} $ 是这些视图的特征矩阵和邻接矩阵。

　　作者使用一个对比目标（即一个判别器），将这两个不同视图中同一节点的表示与其他节点的表示区分开来。

　　对于任何节点  $v_{i}$，它在一 个视图中生成的嵌入  $\boldsymbol{u}_{i}$  被视为 anchor，在另一个视图中生成的节点嵌入 $\boldsymbol{v}_{i}$ 为正样本，在两个视图中除  $v_{i}$  以外的节点表示【假设有  $M$  个 节点，则负样本为  ($2 M-2$x)  个】被视为负样本。定义  $\theta(\boldsymbol{u}, \boldsymbol{v})=s(g(\boldsymbol{u}), g(\boldsymbol{v})) $ ，其中  $s$  为余弦相似度，  $g$  是一个非线性映射（两层的MLP）。

　　我们将每个正对  $\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right)$  的成对目标定义为：

　　　　${\large \ell\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right)=\log \frac{e^{\theta\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right) / \tau}}{\underbrace{e^{\theta\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right) / \tau}}_{\text {the positive pair }}+\underbrace{\sum\limits_{k=1}^{N} \mathbb{1}_{[k \neq i]} e^{\theta\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{k}\right) / \tau}}_{\text {inter-view negative pairs }}+\underbrace{\sum\limits_{k=1}^{N} \mathbb{1}_{[k \neq i]} e^{\theta\left(\boldsymbol{u}_{i}, \boldsymbol{u}_{k}\right) / \tau}}_{\text {intra-view negative pairs }}}} \quad\quad\quad\quad(1)$

　　其中：

• • $\mathbb{1}_{[k \neq i]} \in\{0,1\}$ 是指示函数，当 $k \neq i$ 值为 $1$ ；　　
  • $\tau $ 是温度参数；　　

　　强调一下，本文并没有进行负采样，而是给定正对，负样本对自然而然有其他节点给出。

　　由于两个视图的节点一样，所以另一个视图节点之间的相似性定义为 $\ell\left(\boldsymbol{v}_{i}, \boldsymbol{u}_{i}\right)$ 。

　　最终要最大化的总体目标定义为所有正对的平均值：

　　　　$\mathcal{J}=\frac{1}{2 N} \sum\limits _{i=1}^{N}\left[\ell\left(\boldsymbol{u}_{i}, \boldsymbol{v}_{i}\right)+\ell\left(\boldsymbol{v}_{i}, \boldsymbol{u}_{i}\right)\right]\quad\quad\quad\quad(2)$

　　GRACE 算法流程：

　　

3.2.2 Graph View Generation

　　作者设计了两种图损坏的方法：removing edges 和 masking features 。

Removing edges (RE)

　　在原始图中随机地删除一部分边。形式上，只删除现有的边。

　　首先采样一个随机掩蔽矩阵 $\widetilde{\boldsymbol{R}} \in\{0,1\}^{N \times N}$，矩阵中每个元素依据伯努利分布生成。如果 $\boldsymbol{A}_{i j}=1$ ，则它的值来自伯努利分布 $\widetilde{\boldsymbol{R}}_{i j} \sim \mathcal{B}\left(1-p_{r}\right) $ ，否则 $\widetilde{\boldsymbol{R}}_{i j}=0 $ 。这里的 $p_{r}$ 是每条边被删除的概率。所得到的邻接矩阵可以计算为

　　　　$\widetilde{\boldsymbol{A}}=\boldsymbol{A} \circ \widetilde{\boldsymbol{R}}\quad\quad\quad(3)$

　　其中：$(\boldsymbol{x} \circ \boldsymbol{y})_{i}=x_{i} y_{i}$ 代表着 Hadamard product 。

Masking node features (MF)

　　除了去除边外，我们还在节点特征中用 $0$ 随机屏蔽部分维度\特征。

　　形式上，首先对随机向量  $\widetilde{m} \in\{0,1\}^{F}$  进行采样，其中它的每个维度值都独立地从概率为  $1-p_{m}$  的伯努利分布中提取，即  $\widetilde{m}_{i} \sim   \mathcal{B}\left(1-p_{m}\right) $ 。然后，生成的节点特征  $\widetilde{\boldsymbol{X}}$  为:

　　　　$\tilde{\boldsymbol{X}}=\left[\boldsymbol{x}_{1} \circ \widetilde{\boldsymbol{m}} ; \boldsymbol{x}_{2} \circ \widetilde{\boldsymbol{m}} ; \cdots ; \boldsymbol{x}_{N} \circ \widetilde{\boldsymbol{m}}\right]^{\top}\quad\quad\quad\quad(4)$

　　其中：$[\cdot ;]$ 代表着拼接操作。

　　本文提出的 RE 和 MF 方案在技术上与 Dropout 和 DropEdge 相似，但我们的 GRACE 模型和这两种方法的目的存在根本不同。

• • Dropout 是一种通用的技术，它在训练期间随机屏蔽神经元，以防止大规模模型的过拟合。
  • 在图域中，提出了 DropEdge 来防止 GNN 体系结构过深时的过拟合和缓解过平滑。
  • 然而，我们的 GRACE 框架随机应用 RE 和 MF 生成图拓扑和节点特征层次的对比学习图。此外，在GRACE中使用的GNN编码器是一个相当浅的模型，通常只包含两到三层。

　　在我们的补充内容中，我们共同利用这两种方法来生成视图。  $\tilde{\mathcal{G}}_{1}$  和  $\widetilde{\mathcal{G}}_{2}$  的生成由两个超参数  $p_{r}$  和  $p_{m}$  控制。为了在这两个视图中提供不同的上下文，这两个视图的生成过程使用了两组不同的超参数  $p_{r, 1}$ 、 $p_{m, 1}$  和  $p_{r, 2}$ 、$ p_{m, 2}$  。实验表明，我们的模型对  $p_{r}$  和  $p_{m}$  的选择不敏感，因此原始图没有过度损坏，例如，$p_{r} \leq 0.8$  和  $p_{m} \leq 0.8$  。

3.3 Theoretical Justification

　　Theorem 1. Let  $\mathbf{X}_{i}=\left\{\boldsymbol{x}_{k}\right\}_{k \in \mathcal{N}(i)}$  be the neighborhood of node  $v_{i}$  that collectively maps to its output embedding, where  $\mathcal{N}(i)$  denotes the set of neighbors of node  $v_{i}$  specified by GNN architectures, and  $\mathbf{X}$  be the corresponding random variable with a uniform distribution  $p\left(\mathbf{X}_{i}\right)=\frac{1}{N}$ . Given two random variables  $\mathbf{U}, \mathbf{V} \in \mathbb{R}^{F^{\prime}}$  being the embedding in the two views, with their joint distribution denoted as  $p(\mathbf{U}, \mathbf{V}) $, our objective  $\mathcal{J}$  is a lower bound of  M I  between encoder input  $\mathbf{X}$  and node representations in two graph views  $\mathbf{U}$, $\mathbf{V} $. Formally,

　　　　$\mathcal{J} \leq I(\mathbf{X} ; \mathbf{U}, \mathbf{V})\quad\quad\quad(2)$

4 Experiments

4.1 Datasets

　　

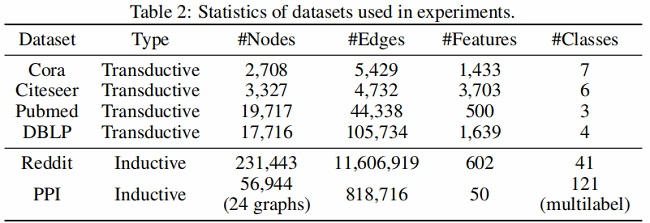
4.2 Experimental Setup

Transductive learning

　　在 Transductive learning 中，使用 $2$ 层的 GCN 作为 encoder：

　　　　$\mathrm{GC}_{i}(\boldsymbol{X}, \boldsymbol{A}) =\sigma\left(\hat{\boldsymbol{D}}^{-\frac{1}{2}} \hat{\boldsymbol{A}} \hat{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{X} \boldsymbol{W}_{i}\right)\quad\quad\quad\quad(7)$

　　　　$f(\boldsymbol{X}, \boldsymbol{A})=\mathrm{GC}_{2}\left(\mathrm{GC}_{1}(\boldsymbol{X}, \boldsymbol{A}), \boldsymbol{A}\right)\quad\quad\quad\quad(8)$

Inductive learning on large graphs

　　考虑到 Reddit 数据的大规模，本文采用具有残差连接的三层 GraphSAGE-GCN 作为编码器，其表述为

　　　　$\widehat{\mathrm{MP}}_{i}(\boldsymbol{X}, \boldsymbol{A}) =\sigma\left(\left[\hat{\boldsymbol{D}}^{-1} \hat{\boldsymbol{A}} \boldsymbol{X} ; \boldsymbol{X}\right] \boldsymbol{W}_{i}\right) \quad\quad\quad\quad(9)$

　　　　$f(\boldsymbol{X}, \boldsymbol{A}) =\widehat{\mathrm{MP}}_{3}\left(\widehat{\mathrm{MP}}_{2}\left(\widehat{\mathrm{MP}}_{1}(\boldsymbol{X}, \boldsymbol{A}), \boldsymbol{A}\right), \boldsymbol{A}\right)\quad\quad\quad\quad(10)$

　　这里使用平均池化传播规则，作为 $\hat{\boldsymbol{D}}^{-1}$ 对节点特征的平均值。由于 Reddit 的大规模，它不能完全融入 GPU 内存。因此，我们应用子采样方法，首先随机选择一批节点，然后通过对节点邻居进行替换，得到以每个所选节点为中心的子图。具体来说，我们分别在 first-, second-, 和 third-hop 采样 30、25、20 个邻居。为了在这种基于采样的设置下生成图视图，RE 和 MF 都可以毫不费力地适应于采样的子图。 

Inductive learning on multiple graphs.

　　对于多图 PPI 的归纳学习，我们叠加了三个具有跳跃连接的平均池化层，类似于 DGI 。图卷积编码器可以表示为

　　　　$\boldsymbol{H}_{1}=\widehat{\mathrm{MP}}_{1}(\boldsymbol{X}, \boldsymbol{A}) \quad\quad\quad\quad(11)$

　　　　$\boldsymbol{H}_{2}=\widehat{\mathrm{MP}}_{2}\left(\boldsymbol{X} \boldsymbol{W}_{\mathrm{skip}}+\boldsymbol{H}_{1}, \boldsymbol{A}\right)\quad\quad\quad\quad(12)$

　　　　$f(\boldsymbol{X}, \boldsymbol{A})=\boldsymbol{H}_{3} =\widehat{\mathrm{MP}}_{3}\left(\boldsymbol{X} \boldsymbol{W}_{\mathrm{skip}}^{\prime}+\boldsymbol{H}_{1}+\boldsymbol{H}_{2}, \boldsymbol{A}\right)\quad\quad\quad\quad(13)$

4.3 Results and Analysis

　　

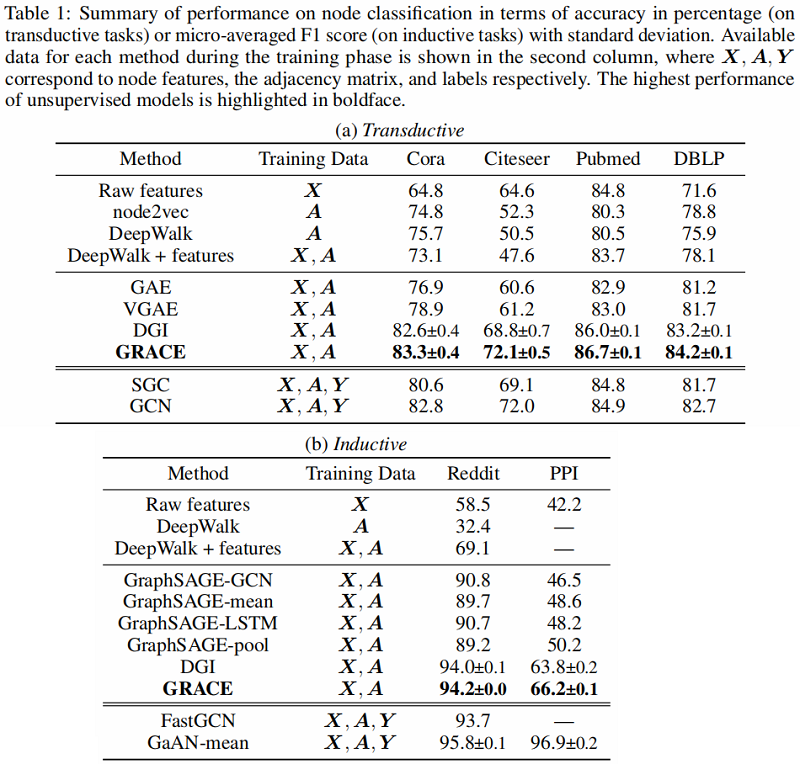
5 Conclusion

　　在本文中，我们开发了一种基于节点级一致性最大化的图对比表示学习框架。我们的模型通过首先使用两种提出的方案生成图视图来学习表示，去除边和屏蔽节点特征，然后应用对比损失来最大限度地提高这两个视图中节点嵌入的一致性。理论分析揭示了从我们的对比目标与互信息最大化和经典的三重态损失之间的联系，这证明了我们的动机。我们在转换和感应设置下使用各种真实数据集进行了全面的实验。实验结果表明，我们提出的方法能够始终大大超过现有的先进方法，甚至超过有监督的转换方法。

 

——————————————————————————————————————————————————

Dataset download links

Cora 
Citeseer 
Pubmed 
DBLP 
Reddit 
PPI