论文解读（GraphCL）《Graph Contrastive Learning with Augmentations》 Learner

1 Paper Information

Title：Graph Contrastive Learning with Augmentations
Authors：Yuning You, Tianlong Chen, Yongduo Sui, Ting Chen, Zhangyang Wang, Yang Shen
Sources：2020, NeurIPS
Others：243 Citations, 74 References
Paper：download
Code：download

---

2 Abstract

　　在本文中，提出了一个图对比学习(GraphCL)框架，用于学习图数据的无监督表示。

　　首先设计了四种类型的图形扩充来合并不同的先验。然后，系统地研究了在四种不同的设置下，图增强的各种组合对多个数据集的影响：半监督、无监督和迁移学习以及对抗性攻击。结果表明即使不使用复杂的GNN架构和数据增强手段，本文提出的GraphCL依然可以得到不错的结果。同时还设计实验验证了不同数据增强手段的效果。

3 Introduction

　　GNN几乎没有自监督的预训练的研究，预训练通常用于训练受梯度消失、爆炸影响的深层影响的任务当中，而大多数研究的图数据集的大小通常受到限制，为了防止 over-smoothing 和信息丢失，GNN结构设置的较浅。但是GNN预训练是十分有意义的。特定于某种图任务的标签往往十分稀缺，而通过预训练可能是一种该问题的解决手段。

　　关于GNN预训练将会越来越有意义：

1. 真实世界的图数据往往是巨大的，即使是基准数据集也变的越来越大；
2. 即使对于浅层模型，预训练也可以更好初始化参数，以更好的寻得局部最小值。

　　与图像数据不同，图是具有多种性质的原始数据的抽象表示，故图形数据中存在各种各样的语义信息，如化学分子结构以及社交网络、推荐网络等，我们很难设计一种对下游任务普遍有利的GNN预训练方案。而针对图任务的naive GNN预训练方案一般为重构顶点的临接信息（如GAE和GraphSAGE）。但这种过于强调邻居的方案并不总是有益的，还可能会损害结构信息。故，我们需要一个设计合理的预训练框架来捕获图结构数据中的高度异构信息。

　　在本文中，针对 GNN 预训练开发了具有数据增强功能的对比学习，以解决图数据的异质性问题。

1. 1. 由于数据增强是进行对比学习的前提，但在图数据中却未得到充分研究，因此本文首先设计四种类型的图数据增强，每种类型都强加了一定的先于图数据，并针对程度和范围进行了参数化；　　
   2. 利用不同的增强手段获得相关视图，提出了一种用于GNN预训练的新颖的图对比学习框架（GraphCL），以便可以针对各种图结构数据学习不依赖于扰动的表示形式；　　
   3. 证明了GraphCL实际上执行了互信息最大化，并且在GraphCL和最近提出的对比学习方法之间建立了联系；　　
   4. 证明了GraphCL可以被重写为一个通用框架，从而统一了一系列基于图结构数据的对比学习方法；　　
   5. 评估在各种类型的数据集上对比不同扩充的性能，揭示性能的基本原理，并为采用特定数据集的框架提供指导；　　
   6. GraphCL在半监督学习，无监督表示学习和迁移学习的设置中达到了最佳的性能，此外还增强了抵抗常见对抗攻击的鲁棒性。　　

4 Methodology

4.1 Data Augmentation for Graphs

　　我们专注于图层级的数据增强。

　　给定 $M$ 个图的数据集中的一个图 $\mathcal{G} \in\left\{\mathcal{G}_{m}: m \in M\right\}$，我们可以构造满足以下条件的增强图

　　　　$\hat{\mathcal{G}} \sim q(\hat{\mathcal{G}} \mid \mathcal{G})$

　　其中 $q(\cdot \mid \mathcal{G})$ 是原始图的增强分布条件，这是预先定义的，代表着数据分布的人类先验。

　　下图是本文总结的4种数据增强手段：

　　　　

1. 节点失活（Node dropping）：随机从图中去除掉部分比例的节点及其边，每个节点的失活概率服从 i.i.d 的均匀分布；
2. 边扰动（Edge perturbation）：随机增加或删除一定比例的边，每个边的增加或者删除的概率亦服从 i.i.d 的均匀分布；
3. 属性屏蔽（Attribute masking）：随机去除部分节点的属性信息，迫使模型使用上下文信息来重新构建被屏蔽的顶点属性。
4. 子图划分（Subgraph）：使用随机游走的方式从G中提取子图的方法。

4.2 图对比学习GraphCL

　　如下图所示，通过潜在空间中的对比损失来最大化同一图的两个扩充view之间的一致性，来进行预训练。

　　　　

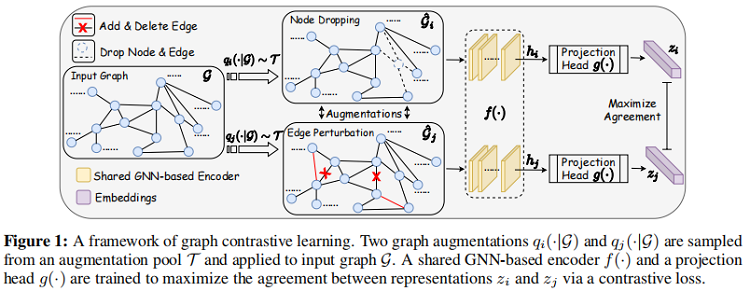
　　模型由4部分组成：

　　1. 图数据增强；

　　2. 基于 GNN 的编码器：

　　聚合步：即信息传递阶段，该阶段会多次执行信息传递过程。

　　其中 图 $G = {V,E}$ 表示无向图，$\mathrm{X} \in \mathrm{R}^{\mathrm{V} \mid \times \mathrm{N}}$  表示特征矩阵，$x_n$  是节点 $V_n$  的 $N$ 维属性向量。

　　考虑 $K$ 层的 GNN，第 $k$ 层的传播表示为：

　　　　$\begin{array}{l} \boldsymbol{a}_{n}^{(k)}=\mathrm{AGGREGATION}^{(k)}\left(\left\{\boldsymbol{h}_{n^{\prime}}^{(k-1)}: n^{\prime} \in \mathcal{N}(n)\right\}\right)\\ \boldsymbol{h}_{n}^{(k)}=\operatorname{COMBINE}^{(k)}\left(\boldsymbol{h}_{n}^{(k-1)}, \boldsymbol{a}_{n}^{(k)}\right)\end{array}$

　　其中：

　　　　$\boldsymbol{h}_{n}^{(k)}$ 是顶点 $V_n$ 在第 $K$ 层的特征矩阵。

　　　　$\boldsymbol{a}_{n}^{(k)}$ 是结点 $V_n$  在第 $k$ 层所接收到的信息。

 　　意义：该公式的意义是节点 $V_n$ 收到的信息来源于节点 $V_n$ 本身状态以及周围节点的信息。

　　读出步：

　　　　$f(\mathcal{G})=\operatorname{READOUT}\left(\left\{\boldsymbol{h}_{n}^{(k)}: v_{n} \in \mathcal{V}, k \in K\right\}\right), \boldsymbol{z}_{\mathcal{G}}=\operatorname{MLP}(f(\mathcal{G}))$

　　通过一个读取函数 READOUT 得到两个视图的图级表示向量 $h_i$ 和 $h_j$ 。

　　3. 投影头：

　　　　一个非线性变换投影头 $g(\cdot )$ ，这里采用双层 MLP ，为将数据增强表示 $h_i$ 和 $h_j$ 转换到潜在空间，分别对应 $\boldsymbol{z}_{i}$，$\boldsymbol{z}_{j}$。

　　4. Contrastive loss：

　　在 GNN 预训练过程中，对一小批  $N$  个图进行随机采样并通过对比学习处理，得到  $2N$  个增广图和相应的对比损失进行优化，我们将小批图中的第  $n$  个图重新注释为  $\boldsymbol{z}_{n, i} ， \boldsymbol{z}_{n, j}$  。负对不是显式采样的，而是来自相同小批中的其他  $N-1$  增广图。将第  $n$  个图的余弦相似函数表示 为  $\operatorname{sim}\left(\boldsymbol{z}_{n, i} ， \boldsymbol{z}_{n, j}\right)=\boldsymbol{z}_{n, i}^{T} \boldsymbol{z}_{n, j} /\left\|\boldsymbol{z}_{n, i}\right\|\left\|\boldsymbol{z}_{n, j}\right\|$  ，第  $n$  个图的 NT-Xent 定义为:

　　　　${\large \ell_{n}=-\log \frac{\exp \left(\operatorname{sim}\left(\boldsymbol{z}_{n, i}, \boldsymbol{z}_{n, j}\right) / \tau\right)}{\sum _{n^{\prime}=1, n^{\prime} \neq n}^{N} \exp \left(\operatorname{sim}\left(\boldsymbol{z}_{n, i}, \boldsymbol{z}_{n^{\prime}, j}\right) / \tau\right)}} $

　　其中 $\tau$ 是 temperature parameter。

　　在不考虑 $\tau$ ，及正确区分正负样本时，即 $z_i$ 与 $z_j$ ( $z_i$ 与 $z_j$ 是 positive pairs）的相似度最高 $sim(z_i,z_i) =1$，且与其他 negative 样本 $z_k$ 的相似度最低 $sim(z_i, z_k) =-1$ ，那么此时公式 $P$ 变成了

　　　　$P=\frac{\exp (1)}{\sum_{k=1}^{ N-1} \exp (-1)+\exp (1)}$

　　观察下图的指数函数的曲线，可以知道当 $N$ 足够大时，$P$ 值是远远小于 $1$ ，趋近 $0$。

　　　　

　　当 $P$ 值远远小于 $1$ 时，想要最大化 $log P$ 的值是比较难的，因为 $P$ 的值代表概率，可以理解成从所有 sample 中找出 positive spamle 的能力 ，在我们假设的最优情况下，它的值是越接近 $1$ 越好。

　　而当我们令 $\tau$ 为一个小数，如 $\tau =0.1$ ，然后令 sim   函数的值除以τ时，相当于在指数函数上做一个linear scaling，此时分子从 exp(1) 变成了 exp(10)。而指数函数的增长速度是非常快的，所以此时

　　　　${\large P=\frac{\exp (10)}{\sum_{k=1}^{2 N-1} \exp (-10)+\exp (10)}} $

　　$P$ 的值是非常近似于 $1$ 的。

5 实验

5.1 数据集

　　这部分实验评估了采用之前提出的四种数据增强方法的图对比学习框架在半监督图分类任务上的效果。在半监督设定下，模型的训练采用 pre-training 加 fine tuning 的方法，采用的数据集包括 Biochemical Molecules 以 及 Social Networks 两类。通过实验得到了文章所提出的预训练方法相对于learn from scratch 方法的性能提升（Figure 2）。

　　　　

　　　　

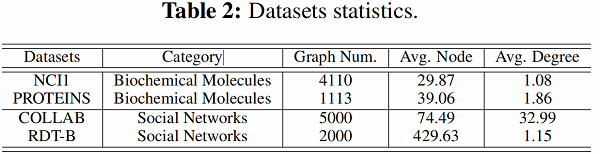
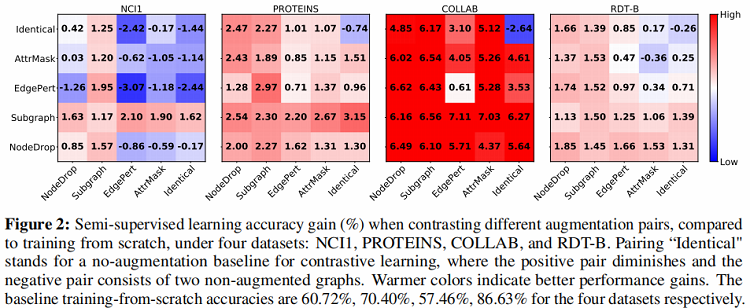
5.2 实验内容

　　实验主要讨论了三部分内容：

　　1、数据增强对于图对比学习的效果具有关键作用

　　A、加入数据增强有效提升了 GraphCL 的效果　　

• • 通过观察 Figure 2 中每个数据图实验结果中的最上一行与最右一列可以发现采用数据增强能有效提升 GraphCL 的分类准确度。这是由于应用适当的数据增强会对数据分布注入相应的先验，通过最大化图与其增强图之间的一致性，使模型学习得到的表示对扰动具有不变性。　　

　　B、组合不同数据增强方式对算法效果提升更大

• • 通过观察 Figure 2 发现每个数据集上采用相同数据增强方式构建的样本对所对应的结果均不是该数据集上的最优结果，而每个数据集上的最优结果均采用不同数据增强组合的方式。文章给出的解释是，采用不同数据增强组合的方式避免了学习到的特征过于拟合低层次的“shortcut”，使特征更加具有泛化性。同时通过 Figure 3 发现当采用不同数据增强方式组合时，相比于单一数据增强时的对比误差下降的更慢，说明不同数据增强组合的方式意味着”更难“的对比学习任务。　　

　　　　

　　2、数据增强的类型，强度以及模式对 GraphCL 效果的影响

　　A、Edge perturbation 的方式对于 Social Network 有效但在部分 biochemical Molecules 数据集上反而有负面效果

　　通过 Figure 2 可以看出Edge perturbation的数据增强方式在除 NCI1 之外的三个数据集上均有较好的效果，但是在 NCI1 上的效果反而比 baseline 算法差。这是由于对 NCI1 中的网络的语义对于边的扰动更加敏感，对网络中边进行修改可能会改变分子的性质从而破坏网络语义，进而影响下游任务。针对 Edge perturbation 的强度，从 Figure 4 中可以得出，在 COLLAB 数据集上，算法性能随 Edge perturbation 的强度增加而提升，但在 NCI1 数据集上，Edge perturbation 强度对算法效果无明显影响。

　　　　

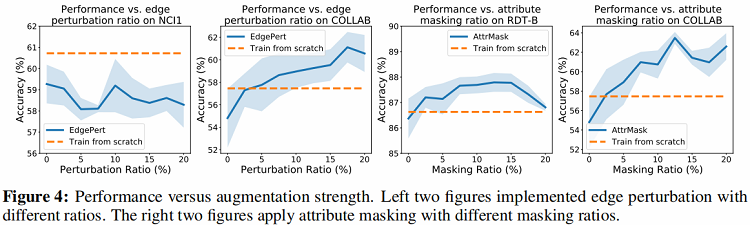
　　B、Attribute masking的方式在更“密集“的图数据上能取得更好效果

　　从 Figure 2 中可以发现Attribute masking的增强方式在平均度更高的数据集上具有更好的性能增益（例如COLLAB），而在平均度较低的数据集上增益明显减小。文章对这个结果做出的假设是，当图数据越密集时，意味着 Attribute masking 之后模型仍然有足够的其他数据来重建被屏蔽的数据，而反之则难以重建。在强度方面，通过增加Attribute masking的强度可以在更“密集”的数据集上提升算法效果。

　　C、Node dropping 和 Subgraph 的方式对所有数据集都有效

　　上述两种方式，尤其是 Subgraph 的数据增强方式在实验中的数据集上都能给图对比学习算法带来性能增益。Node dropping有效的原因是，在许多图数据中去掉部分节点并不影响整图的语义。而对于 Subgraph 的方式，之前的相关研究已经说明了采用 Local-Global 的对比学习方式训练图表示是有效的。

　　3、相对于“更难”的任务，过于简单的对比任务对算法性能提升没有帮助

“更难”的任务有利于提升GraphCL的效果，这里包含两种情况，一种是将不同的数据增强方法进行组合，另一种是增加数据增强的强度或者提高增强模式的难度，例如采用更高的概率进行Node dropping，或者采用均匀分布之外的复杂分布进行 Node dropping。

5.3 GraphCL与SOTA算法的性能对比

　　在这部分实验中，文章对比了 GraphCL 与 SOTA 的图表示方法在四种setting下的图分类任务中的性能，包括半监督、无监督、迁移学习以及对抗攻击setting。具体实验设置详见原文。在半监督、无监督、迁移学习任务中，GraphCL 在大部分数据集上的分类准确率都达到了 SOTA ，在对抗攻击setting下，实验结果表明GraphCL增强了模型的鲁棒性。

　　1.半监督任务

　　

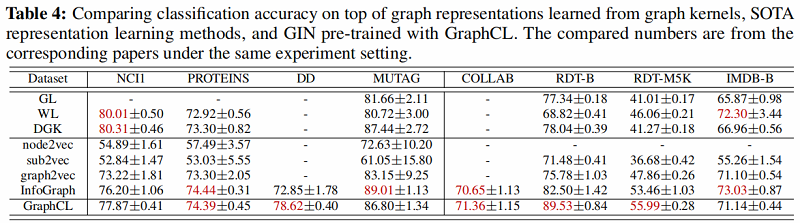
　　2. 无监督任务

　　比较从图核学习的图表示、SOTA 表示学习方法和用 GraphCL 预训练的 GIN 的分类精度。

　　

　　3.  迁移学习任务

　　不同人工设计预训练方案的迁移学习比较

　　

　　4.对抗鲁棒性测试任务

　　GNN在三种不同深度对抗攻击下的对抗性能

　　

Conclusion

　　在本文中，我们探索针对GNN预训练的对比学习，因为它面临着图结构化数据中的独特挑战。 首先，提出了几种图形数据扩充方法，并在介绍某些特定的人类数据分布先验的基础上进行了讨论。 随着新的扩充，我们为GNN预训练提出了一种新颖的图对比学习框架（GraphCL），以促进不变表示学习以及严格的理论分析。 我们系统地评估和分析了我们提出的框架中数据扩充的影响，揭示了其原理并指导了扩充的选择。 实验结果验证了我们提出的框架在通用性和鲁棒性方面的最新性能。