127. 单词接龙
给定两个单词(beginWord 和 endWord)和一个字典,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典中的单词。
说明:
如果不存在这样的转换序列,返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的,且二者不相同。
示例 1:
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
输出: 5
解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",
返回它的长度 5。
示例 2:
输入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
输出: 0
解释: endWord "cog" 不在字典中,所以无法进行转换。
拥有一个 beginWord 和一个 endWord,分别表示图上的 start node 和 end node。我们希望利用一些中间节点(单词)从 start node 到 end node,中间节点是 wordList 给定的单词。我们对这个单词接龙每个步骤的唯一条件是相邻单词只可以改变一个字母。
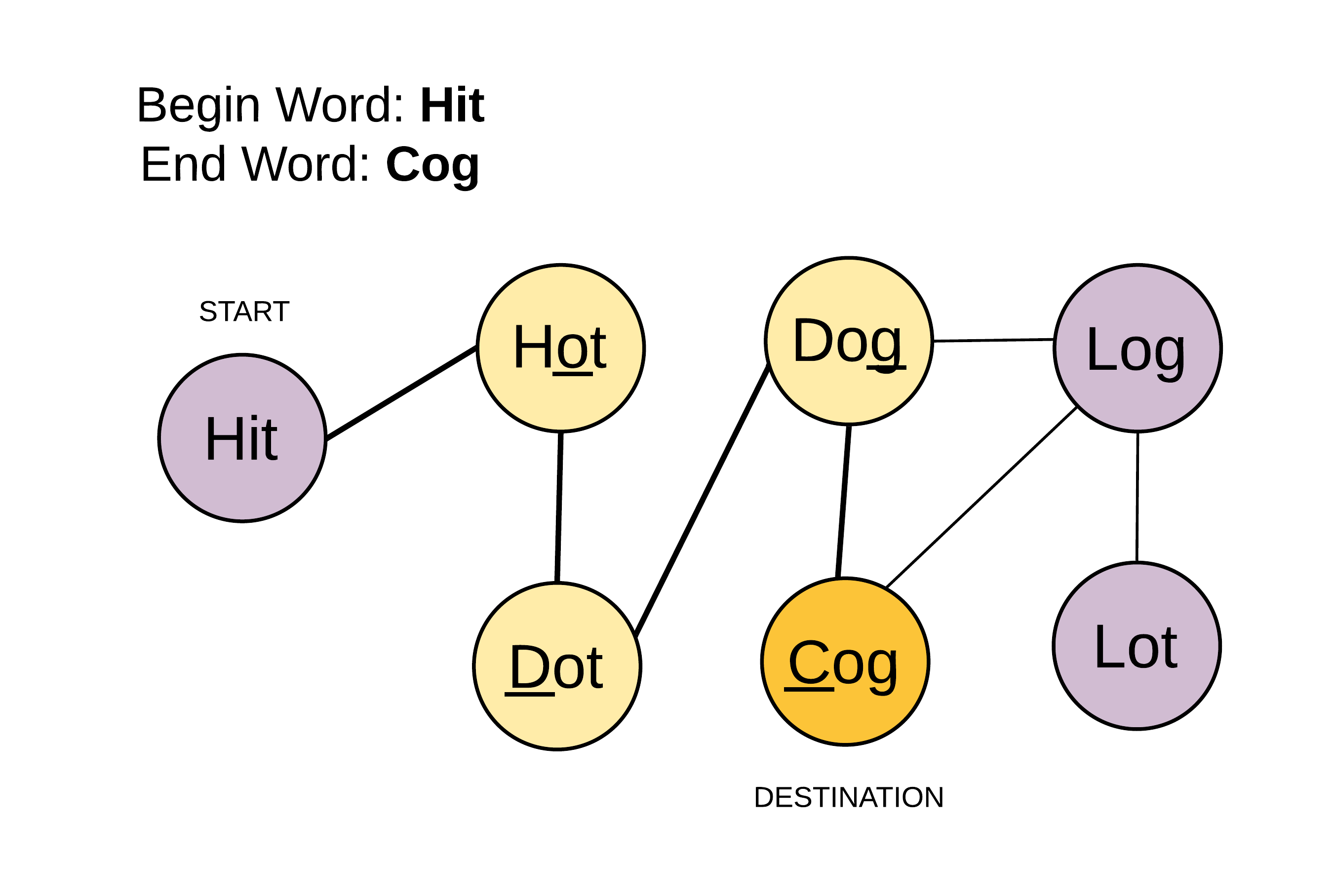
我们将问题抽象在一个无向无权图中,每个单词作为节点,差距只有一个字母的两个单词之间连一条边。问题变成找到从起点到终点的最短路径,如果存在的话。因此可以使用广度优先搜索方法。
算法中最重要的步骤是找出相邻的节点,也就是只差一个字母的两个单词。为了快速的找到这些相邻节点,我们对给定的 wordList 做一个预处理,将单词中的某个字母用 * 代替。
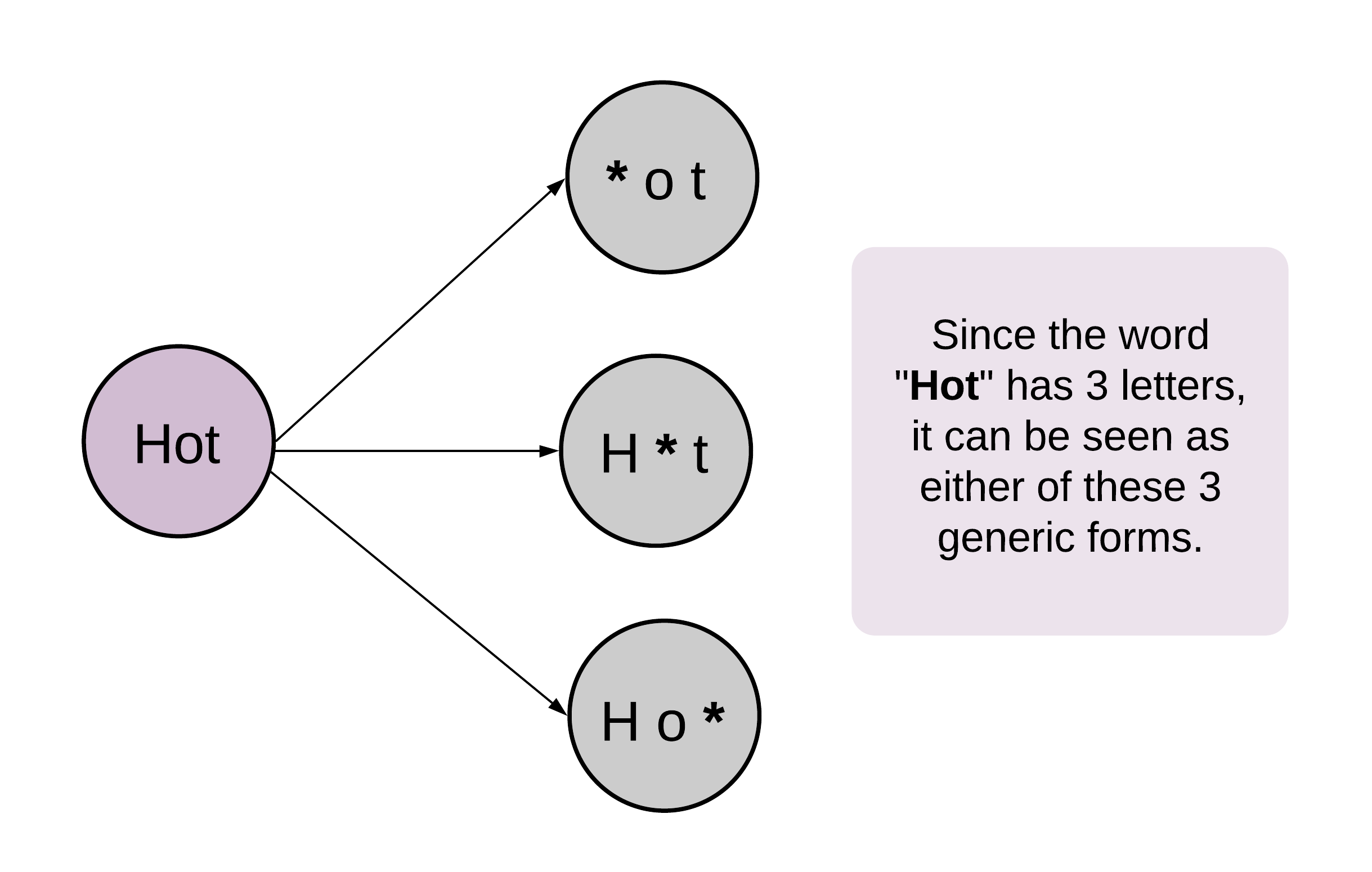
这个预处理帮我们构造了一个单词变换的通用状态。例如:Dog ----> D*g <---- Dig,Dog 和 Dig 都指向了一个通用状态 D*g。
这步预处理找出了单词表中所有单词改变某个字母后的通用状态,并帮助我们更方便也更快的找到相邻节点。否则,对于每个单词我们需要遍历整个字母表查看是否存在一个单词与它相差一个字母,这将花费很多时间。预处理操作在广度优先搜索之前高效的建立了邻接表。
例如,在广搜时我们需要访问 Dug 的所有邻接点,我们可以先生成 Dug 的所有通用状态:
Dug => *ug
Dug => D*g
Dug => Du*
第二个变换 D*g 可以同时映射到 Dog 或者 Dig,因为他们都有相同的通用状态。拥有相同的通用状态意味着两个单词只相差一个字母,他们的节点是相连的。
方法 1:广度优先搜索想法
利用广度优先搜索搜索从 beginWord 到 endWord 的路径。
算法
对给定的 wordList 做预处理,找出所有的通用状态。将通用状态记录在字典中,键是通用状态,值是所有具有通用状态的单词。
将包含 beginWord 和 1 的元组放入队列中,1 代表节点的层次。我们需要返回 endWord 的层次也就是从 beginWord 出发的最短距离。
为了防止出现环,使用访问数组记录。
当队列中有元素的时候,取出第一个元素,记为 current_word。
找到 current_word 的所有通用状态,并检查这些通用状态是否存在其它单词的映射,这一步通过检查 all_combo_dict 来实现。
从 all_combo_dict 获得的所有单词,都和 current_word 共有一个通用状态,所以都和 current_word 相连,因此将他们加入到队列中。
对于新获得的所有单词,向队列中加入元素 (word, level + 1) 其中 level 是 current_word 的层次。
最终当你到达期望的单词,对应的层次就是最短变换序列的长度。
标准广度优先搜索的终止条件就是找到结束单词。
代码:
class Solution{
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList){
//加入所有节点,访问过一次,删除一个。
set<string> s;
for (int i = 0; i < wordList.size(); i++)
s.insert(wordList[i]);
queue<pair<string, int> > q;
//加入beginword
q.push( pair<string, int>( beginWord, 1) );
string tmp; //每个节点的字符
int step; //抵达该节点的step
while ( !q.empty() ){
if ( q.front().first == endWord){
return (q.front().second);
}
tmp = q.front().first;
step = q.front().second;
q.pop();
//寻找下一个单词了
char ch;
for (int i = 0; i < tmp.length(); i++){
ch = tmp[i];
for (char c = 'a'; c <= 'z'; c++){
//从'a'-'z'尝试一次
if ( ch == c) continue;
tmp[i] = c ;
//如果找到的到
if ( s.find(tmp) != s.end() ){
q.push(pair<string, int>(tmp, step+1));
s.erase(tmp) ; //删除该节点
}
tmp[i] = ch; //复原
}
}
}
return 0;
}
};

方法 2:双向广度优先搜索想法
根据给定字典构造的图可能会很大,而广度优先搜索的搜索空间大小依赖于每层节点的分支数量。假如每个节点的分支数量相同,搜索空间会随着层数的增长指数级的增加。考虑一个简单的二叉树,每一层都是满二叉树的扩展,节点的数量会以 2 为底数呈指数增长。
如果使用两个同时进行的广搜可以有效地减少搜索空间。一边从 beginWord 开始,另一边从 endWord 开始。我们每次从两边各扩展一个节点,当发现某一时刻两边都访问了某一顶点时就停止搜索。这就是双向广度优先搜索,它可以可观地减少搜索空间大小,从而降低时间和空间复杂度。
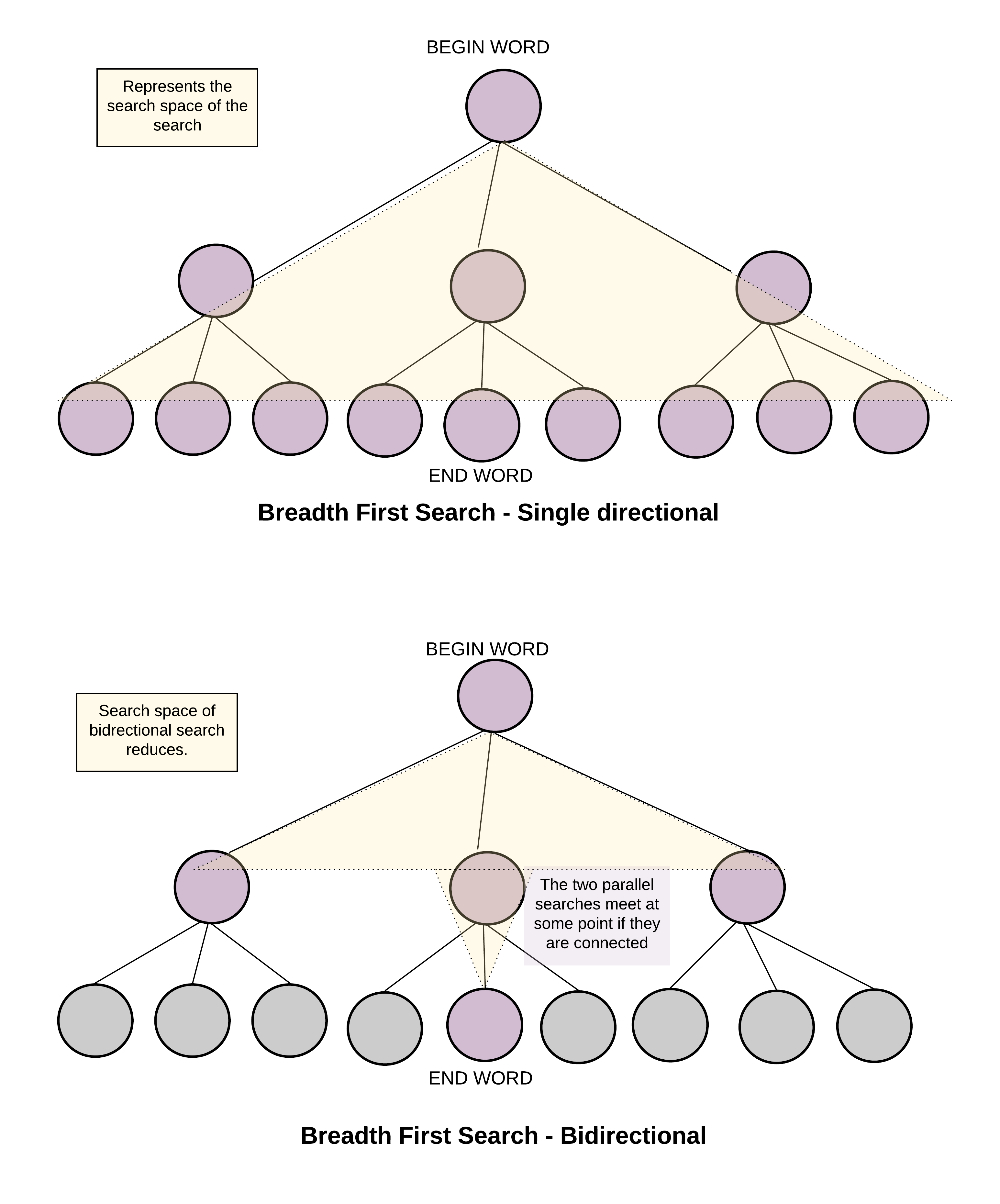
算法
算法与之前描述的标准广搜方法相类似。
唯一的不同是我们从两个节点同时开始搜索,同时搜索的结束条件也有所变化。
我们现在有两个访问数组,分别记录从对应的起点是否已经访问了该节点。
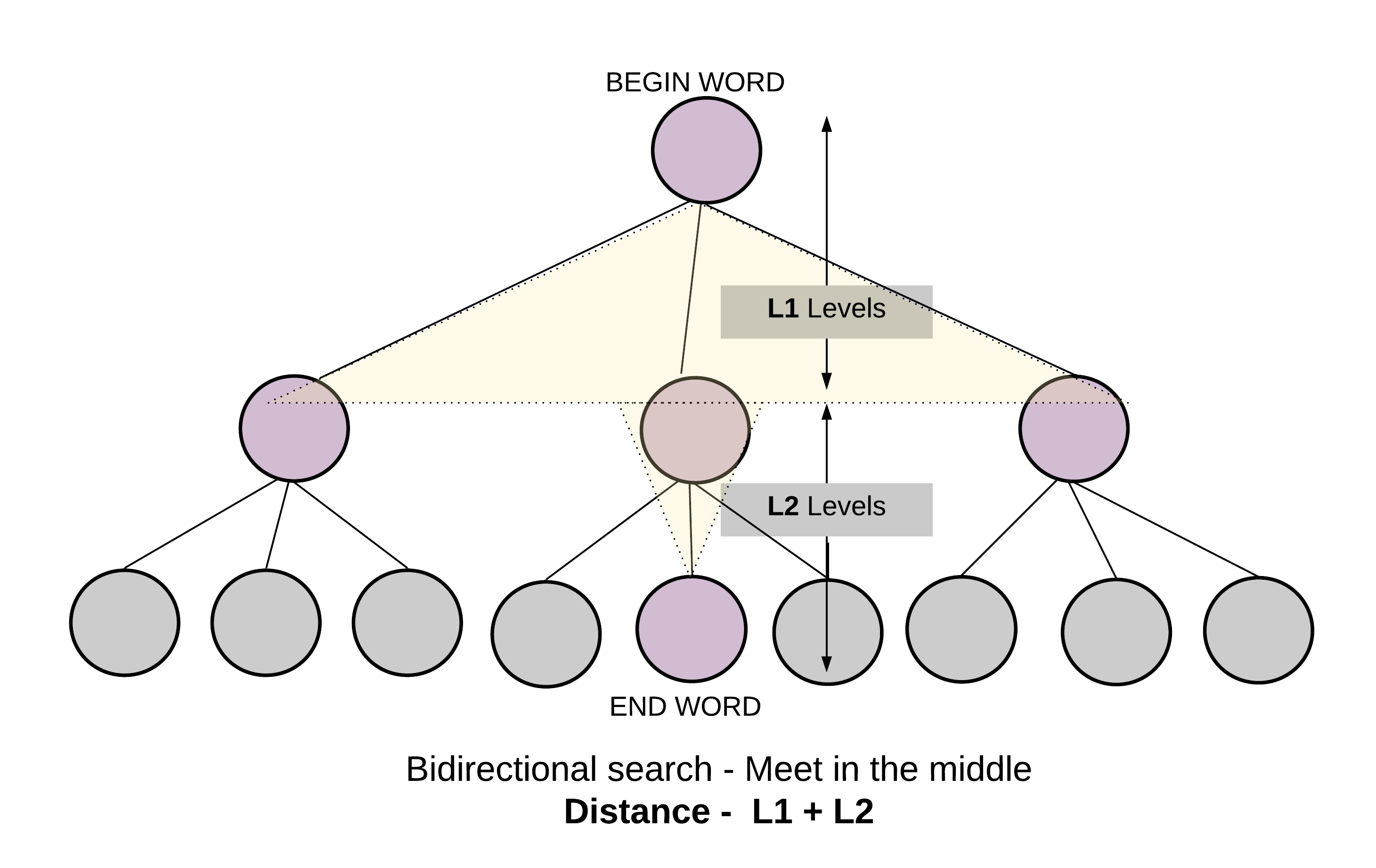
如果我们发现一个节点被两个搜索同时访问,就结束搜索过程。因为我们找到了双向搜索的交点。过程如同从中间相遇而不是沿着搜索路径一直走。
双向搜索的结束条件是找到一个单词被两边搜索都访问过了。
最短变换序列的长度就是中间节点在两边的层次之和。因此,我们可以在访问数组中记录节点的层次。
代码:
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
unordered_set<string> dict(wordList.begin(), wordList.end());
if (dict.find(endWord) == dict.end() ) return 0;
// 初始化起始和终点
unordered_set<string> beginSet, endSet, tmp, visited;
beginSet.insert(beginWord);
endSet.insert(endWord);
int len = 1;
while (!beginSet.empty() && !endSet.empty()){
if (beginSet.size() > endSet.size()){
tmp = beginSet;
beginSet = endSet;
endSet = tmp;
}
tmp.clear();
for ( string word : beginSet){
for (int i = 0; i < word.size(); i++){
char old = word[i];
for ( char c = 'a'; c <= 'z'; c++){
if ( old == c) continue;
word[i] = c;
if (endSet.find(word) != endSet.end()){
return len+1;
}
if (visited.find(word) == visited.end() && dict.find(word) != dict.end()){
tmp.insert(word);
visited.insert(word);
}
}
word[i] = old;
}
}
beginSet = tmp;
len++;
}
return 0;
}
};